Ортогональные проекции
Ошибка.
Попробуйте повторить позже
Найдите площадь сечения правильной шестиугольной пирамиды плоскостью, проходящей через вершину
основания
и параллельной медиане
боковой грани
и апофеме
боковой грани
если сторона основания пирамиды
равна
а расстояние от вершины
до секущей плоскости равно
Источники:
Подсказка 1
Итак, перед нами стереометрия с ШВБ, технической олимпиады, а значит придётся много считать и не бояться этого. Но для того, чтобы найти площадь сечения, нужно сначала его построить, что не очень просто, ведь пирамида аж шестиугольная. Однако нам дано целых две прямые, параллельные сечению, поэтому, хорошей идеей для начала решения будет постpоение разных прямых, параллельных данным в некоторых плоскостях.
Подсказка 2
Построим прямую SQ, параллельную CM, точка Q принадлежит CD. Что теперь можно сказать про отношение плоскостей SQN и сечения?
Подсказка 3
Они параллельны! Через точку F проведём прямую, параллельную NQ, пусть она пересекает CD в точкe V. Правда ли, что эта прямая принадлежит сечению?
Подсказка 4
Да, это верно! Через точку V проведем прямую VL, параллельную CM, L лежит на SC. Получается, плоскость FVL — плоскость сечения. Теперь нетрудно найти точки, в которых эта плоскость пересекает плоскость пирамиды.
Подсказка 5
Ура, мы построили сечение! Но получился пятиугольник, как теперь искать его площадь? Вспомните формулу: Площадь сечения равна площади проекции сечения на основание делить на угол между плоскостями сечения и основания.
Подсказка 6
Дальше дело техники! Площадь проекции найдите как сумму площадей треугольников. Длины различных отрезков можно искать и выражать через длину стороны основания с помощью подобия, теоремы Фалеcа. Не забывайте так же про большое количество параллельных прямых на чертеже и правильность шестиугольника в основании. А для того, чтобы найти угол, нужно вспомнить про данное в условии расстояние!
Построим сечение пирамиды. В плоскости через точку
проведем прямую
параллельную
принадлежит прямой
Тогда
будет средней линией треугольника
следовательно,
где
— сторона основания
пирамиды.
Плоскость содержит прямые
и
которые параллельны плоскости сечения, следовательно, по признаку плоскость
параллельна плоскости сечения.
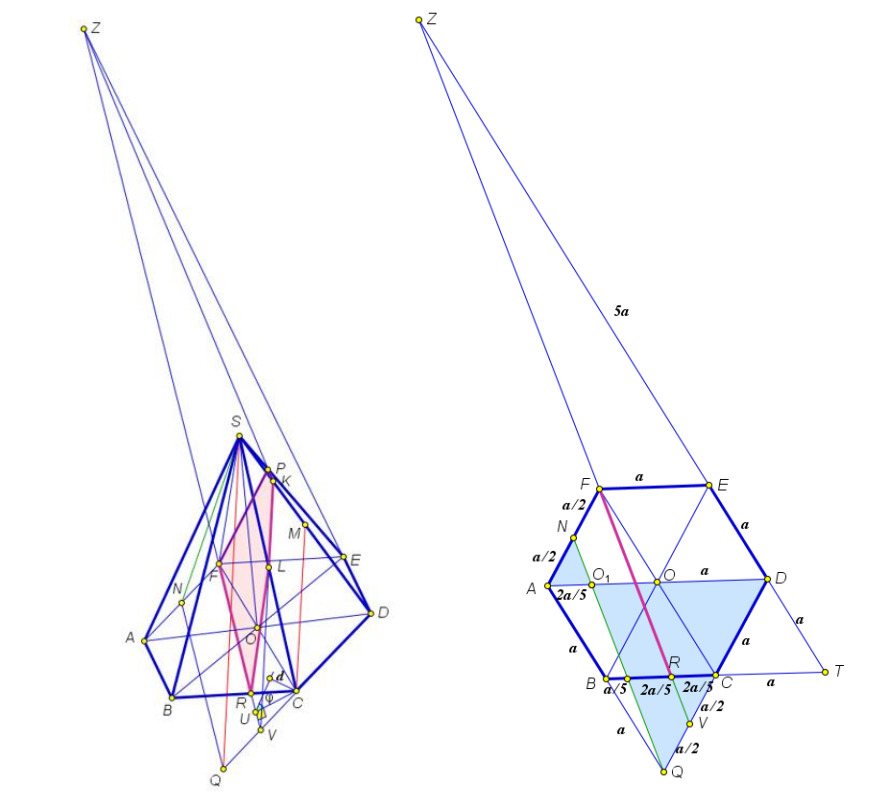
Через точку проведем прямую
параллельную
где
принадлежит прямой
Т.к.
и
значит,
— параллелограмм, следовательно,
Учитывая, что
— середина
а также
можем
сказать, что
Пусть — точка пересечения прямых
и
Плоскость сечения пересекает основание пирамиды по отрезку
Пусть — точка пересечения
и
Заметим, что углы
И
равны как вертикальные, а углы
и
как накрестлежащие при параллельных прямых
и
и секущей
Следовательно, треугольники
и
подобны,
поэтому
Т.к. является правильным шестиугольником, значит,
Учитывая, что
получаем,
что
Т.к.
и
углы
и
равны, аналогично, т.к.
и
углы
и
равны, а также
следовательно, треугольники
и
равны, поэтому
Пусть точка — точка пересечения прямых
и
а точка
— точка пересечения прямых
и
Из-за того, что
— правильный шестиугольник, можно сделать вывод, что
Т.к.
треугольники
и
подобны, поэтому
В плоскости через точку
проведем прямую
параллельную
принадлежит ребру
— точка пересечения
прямой
с ребром
параллельны друг другу, поэтому по теореме Фалеса имеем
В плоскости точка
— точка пересечения прямых
и
Запишем теорему Менелая для треугольника
и секущей
Искомое сечение - это Для нахождения площади сечения используем формулу
где — площадь проекции сечения на плоскость основания,
— угол между плоскостью сечения и плоскостью основания. Найдем
площадь проекции сечения на плоскость основания.
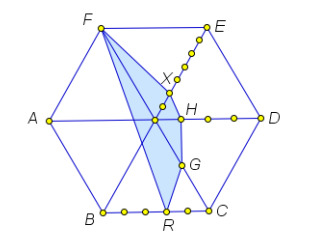
Проекцией является пятиугольник Площадь проекции сечения вычисляется по формуле
Обозначим расстояние от точки до плоскости сечения
Т.к. точка
принадлежащая плоскости сечения является
серединой
расстояние от точки
до сечения тоже равно
В треугольнике
проведем высоту
обозначим ее длину
Тогда
Т.к. — правильный,
Тогда найдем
по теореме косинусов:
Используя различные формулы для нахождения площади треугольника имеем
Тогда
Окончательно имеем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




