Тема Счёт площадей и объёмов

Ортогональные проекции

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт площадей и объёмов

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#69311

Найдите площадь сечения правильной шестиугольной пирамиды $SABCDEF$ плоскостью, проходящей через вершину $F$ основания $ABCDEF$ и параллельной медиане $CM$ боковой грани $SCD$ и апофеме $SN$ боковой грани $SAF,$ если сторона основания пирамиды равна $√- 4 7,$ а расстояние от вершины $S$ до секущей плоскости равно $√- 7.$

Источники: ШВБ-2023, 11.6 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

Итак, перед нами стереометрия с ШВБ, технической олимпиады, а значит придётся много считать и не бояться этого. Но для того, чтобы найти площадь сечения, нужно сначала его построить, что не очень просто, ведь пирамида аж шестиугольная. Однако нам дано целых две прямые, параллельные сечению, поэтому, хорошей идеей для начала решения будет постpоение разных прямых, параллельных данным в некоторых плоскостях.

Подсказка 2

Построим прямую SQ, параллельную CM, точка Q принадлежит CD. Что теперь можно сказать про отношение плоскостей SQN и сечения?

Подсказка 3

Они параллельны! Через точку F проведём прямую, параллельную NQ, пусть она пересекает CD в точкe V. Правда ли, что эта прямая принадлежит сечению?

Подсказка 4

Да, это верно! Через точку V проведем прямую VL, параллельную CM, L лежит на SC. Получается, плоскость FVL — плоскость сечения. Теперь нетрудно найти точки, в которых эта плоскость пересекает плоскость пирамиды.

Подсказка 5

Ура, мы построили сечение! Но получился пятиугольник, как теперь искать его площадь? Вспомните формулу: Площадь сечения равна площади проекции сечения на основание делить на угол между плоскостями сечения и основания.

Подсказка 6

Дальше дело техники! Площадь проекции найдите как сумму площадей треугольников. Длины различных отрезков можно искать и выражать через длину стороны основания с помощью подобия, теоремы Фалеcа. Не забывайте так же про большое количество параллельных прямых на чертеже и правильность шестиугольника в основании. А для того, чтобы найти угол, нужно вспомнить про данное в условии расстояние!

Показать ответ и решение

Построим сечение пирамиды. В плоскости $SCD$ через точку $S$ проведем прямую $SQ,$ параллельную $CM,$ $Q$ принадлежит прямой $CD.$ Тогда $CM$ будет средней линией треугольника $SQD,$ следовательно, $QC = CD = a,$ где $a$ — сторона основания пирамиды.

Плоскость $SNQ$ содержит прямые $SN$ и $SQ,$ которые параллельны плоскости сечения, следовательно, по признаку плоскость $SNQ$ параллельна плоскости сечения.

$PIC$

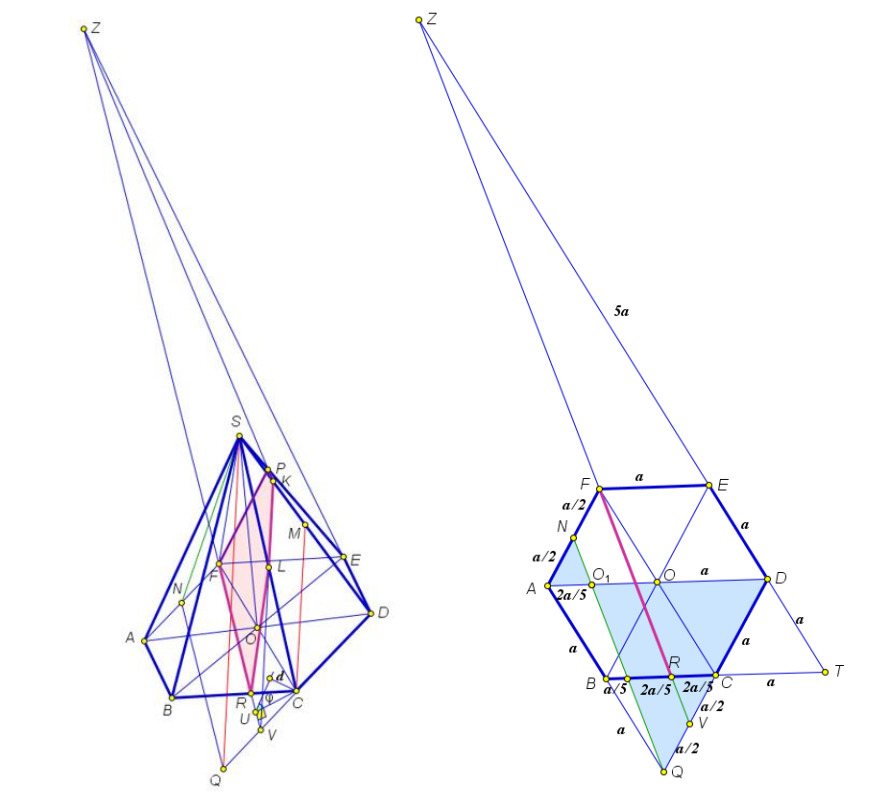
Через точку $F$ проведем прямую $FV,$ параллельную $NQ,$ где $V$ принадлежит прямой $CQ.$ Т.к. $AF ∥CD$ и $NQ ∥F V,$ значит, $NF VQ$ — параллелограмм, следовательно, $NF = QV.$ Учитывая, что $N$ — середина $AF,$ а также $V C = QC − QV =a − QV,$ можем сказать, что $QV = VC =a∕2.$

Пусть $R$ — точка пересечения прямых $FV$ и $BC.$ Плоскость сечения пересекает основание пирамиды по отрезку $FR.$

Пусть $O 1$ — точка пересечения $NQ$ и $AD.$ Заметим, что углы $AO N 1$ И $DO Q 1$ равны как вертикальные, а углы $NAO 1$ и $O DQ 1$ как накрестлежащие при параллельных прямых $AF$ и $CD$ и секущей $AD.$ Следовательно, треугольники $AO N 1$ и $DO Q 1$ подобны, поэтому

AO1- AN- a∕2 1 O1D = QD = 2a = 4

Т.к. $ABCDEF$ является правильным шестиугольником, значит, $AD = 2a.$ Учитывая, что $AO1 :O1D =1 :4,$ получаем, что $AO1 = 2a∕5.$ Т.к. $AD ∥BC$ и $AF ∥ CD,$ углы $RCV$ и $O1AN$ равны, аналогично, т.к. $AF ∥CD$ и $FV ∥NQ,$ углы $RV C$ и $O1NA$ равны, а также $AN = VC =a∕2,$ следовательно, треугольники $RCV$ и $O1AN$ равны, поэтому $RC = AO1 =2a∕5.$

Пусть точка $Z$ — точка пересечения прямых $RF$ и $DE,$ а точка $T$ — точка пересечения прямых $BC$ и $DE.$ Из-за того, что $ABCDEF$ — правильный шестиугольник, можно сделать вывод, что $CT =DT = a.$ Т.к. $F E ∥ BC,$ треугольники $FZE$ и $RZT$ подобны, поэтому

ZE-= --ZE---= FE-= --a----= 5⇒ ZE = 5a ZT ZE +2a RT 2a∕5+ a 7

В плоскости $SCD$ через точку $V$ проведем прямую $V K,$ параллельную $CM,$ $K$ принадлежит ребру $SD,$ $L$ — точка пересечения прямой $V K$ с ребром $SC.$ $CM, VK,SQ$ параллельны друг другу, поэтому по теореме Фалеса имеем

SK-- SK- 1 SK :KM :MD = QV :V C :CD = 1:1 :2 ⇒ KM = 1 и KD = 3

SL SK LC-= KM--=1

В плоскости $SDE$ точка $P$ — точка пересечения прямых $ZK$ и $SE.$ Запишем теорему Менелая для треугольника $SDE$ и секущей $KZ$

DKKS ⋅ SPPE-⋅ EZZD-= 1

3⋅ SP-⋅ 5= 1 PE 6

SP-= 2 PE 5

Искомое сечение - это $KLRF P.$ Для нахождения площади сечения используем формулу

Sсеч =-Sпр-, cosφ

где $Sпр$ — площадь проекции сечения на плоскость основания, $φ$ — угол между плоскостью сечения и плоскостью основания. Найдем площадь проекции сечения на плоскость основания.

$PIC$

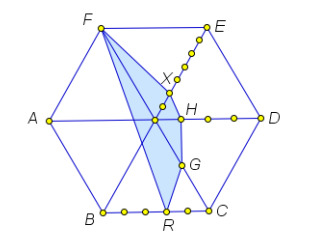
Проекцией является пятиугольник $TXHJR.$ Площадь проекции сечения вычисляется по формуле

Sпр = SFRG +SOGH + SOHX +SOXF

a2√3 2 1 a2√3 1 1 a2√3 1 2 a2√3 2 a2√3 Sпр = 5 − 5 ⋅2 ⋅ 4 + 2 ⋅4 ⋅ 4 +4 ⋅7 ⋅ 4 + 7 ⋅ 4

2√ - √ - Sпр = 30335a⋅323= 30130-3

Обозначим расстояние от точки $S$ до плоскости сечения $d,$ $√- d= 7.$ Т.к. точка $L,$ принадлежащая плоскости сечения является серединой $SC,$ расстояние от точки $C$ до сечения тоже равно $d.$ В треугольнике $RCV$ проведем высоту $CU,$ обозначим ее длину $h.$ Тогда

∘-------- sinφ= d ⇒ cosφ = 1− (d)2 h h

Т.к. $ABCDEF$ — правильный, $∘ ∠RCV = 60 .$ Тогда найдем $RV$ по теореме косинусов:

2 2 2 2 √ -- RV 2 = 4a-+ a-− a = 21a-⇒ RV =--21a 25 4 5 100 10

Используя различные формулы для нахождения площади треугольника $RCV,$ имеем

√-- √- -21ah= a2 ⋅-3⇒ h= a√-- 10 5 2 7

Тогда

∘ ----2- cosφ= 1− 7d2-= 3 a 4

Окончательно имеем

303√3 √- S = --10--= 202-3- сеч 3 5 4

Ответ:

$202√3 5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#38769

Докажите, что если все плоские углы при некоторой вершине тетраэдра прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площадей всех остальных граней тетраэдра.

[Пространственный аналог теоремы Пифагора для прямого тетраэдра]

Подсказки к задаче

Подсказка 1

Попробуйте провести прямую к вершине, при которой все плоские углы прямые! Что хорошего можно сказать про получившиеся углы? А про их косинусы?

Подсказка 2

Каждый косинус можно записать как отношение проекции отрезка, лежащего на прямой к самому отрезку! Что можно сказать про сумму квадратов всех косинусов?

Подсказка 3

Да, сумма квадратов косинусов этих углов равна единице! Однако на грани мы пока так и не вышли... А если применить теорему о площади ортогональной проекции? Можно ли выразить площадь грани, противолежащей вершине (у которой все плоские углы прямые), через площади остальных граней?

Подсказка 4

Да, S1/S2 = cos(x). Отношение таких площадей равно одному из косинусов, которые получились при проведении нашей прямой! Тогда что осталось сделать, чтобы доказать требуемое?

Показать ответ и решение

$PIC$

Пусть это углы при вершине $D$ в тетраэдре $ABCD$ . То есть нужно доказать, что

S2ABC = S2ACD +S2ABD + S2BCD

Пусть $∠ADO = α,∠BDO = β,∠CDO =γ$ . Отсюда $cos2α +cos2β +cos2γ = 1$ (по сути это сумма квадратов проекций $DO$ на “оси координат” — стороны тетраэдра, делённая на само $DO2$ , что равно единице из теоремы Пифагора).

По теореме о площади ортогональной проекции $SBCD =SABC ⋅cosα.$ Выписывая аналогичные равенства для оставшихся граней, получаем нужное соотношение $S2ABC =S2ACD + S2ABD+ S2BCD.$

Ответ:

что и требовалось доказать

Ошибка.
Попробуйте повторить позже

Задача 3#63892

Из вершины $D$ на плоскость основания $ABC$ пирамиды $ABCD$ опущена высота $DH$ . Найдите объем этой пирамиды, если известно, что площади треугольников $△HBC, △HAC, △HAB$ равны соответственно $2 1 4 9,3,9$ , и что все три плоских угла при вершине $D$ прямые.

Источники: ДВИ - 2017, вариант 1, задача 7 (cpk.msu.ru)

Подсказки к задаче

Подсказка 1

У нас на картинке очень много прямых углов и даны площади, поэтому хочется попользоваться формулой площади проекции. Посмотрим: △BHC- ортогональная проекция треугольника △BDC, а треугольник △BDC, в свою очередь- ортогональная проекция треугольника △BAC. Какими тогда формулами связаны площади этих треугольников?

Подсказка 2

Выписав соотношения этих площадей через косинус двугранного угла, нетрудно увидеть, что S²(△BDC)= S(△BAC)*S(△BHC). Учитывая, что S(△BAC) = 1, получаем: S(△BDC) = √S(△BHC). Абсолютно аналогично для остальных граней. Как думаете, сможем ли мы, зная площади боковых граней, найти объем тетраэдра?

Подсказка 3

Кончено сможем! V = 1/6 * AD*CD*BD. Учитывая, что боковые грани- прямоугольные треугольники, выразите их площади через катеты и преобразуйте предыдущее выражение. Я в вас верю!

Показать ответ и решение

Обозначим через $α,β,γ$ двугранные углы при ребрах $BC,AC,AB$ соответственно. Поскольку $DH ⊥ ABC,△HBC$ является ортогональной проекцией $△DBC$ .

$PIC$

Следовательно, $SS(△(△HDBBCC-)) = cosα$ . С другой стороны, $AD ⊥ DBC$ , то есть $△DBC$ является ортогональной проекцией $△ABC$ , откуда

S(△DBC--)= cosα. S(△ABC )

Учитывая, что $S(△ABC )= S(△ABH )+S (△BCH )+S(△ACH )= 1$ , получаем

S(△HBC-) ∘ -------- cosα =S(△DBC )= S(△DBC ) = S(△HBC ).

Аналогично,

∘-------- cosβ = S(△DAC )= ∘S(△HAC-) cosγ = S(△DAB )= S(△HAB )

Далее, поскольку плоские углы при вершине $D$ прямые,

1 √2∘ BD-⋅CD--AD-⋅CD--AD-⋅BD- V (ABCD )= 6AD ⋅BD ⋅CD = -3- ---2---⋅---2---⋅---2---=

√-∘ -------------------------- √-∘ -------------------------- = -2- S(△DBC )⋅S(△DAC )⋅S(△DAB )= -24 S(△HBC )⋅S(△HAC )⋅S(△HAB )= 3 3

√ -∘ ------- √- = --24 2⋅ 1 ⋅ 4= 24√9 3 9 3 9 43

Ответ:

$2√√42 9 43$

Ошибка.
Попробуйте повторить позже

Задача 4#63899

В правильном тетраэдре $ABCD$ проведено сечение так, что оно проходит через точки $K,L,M$ , лежащие на ребрах $DC,DB, DA$ соответственно. При этом $DK :KC = 1:3,DL :LB = 2:1,DM :MA =1 :1$ . Найдите угол между плоскостями грани $ABC$ и построенного сечения.

Источники: ПВГ-2014, 11.5 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Аккуратно построим картинку. Кажется, тут явным образом никак не построить линейный угол... Будем искать обходные пути: теорема о площади ортогональной проекции нам поможет! Тетраэдр правильный, поэтому высота к грани АВС будет падать в центр правильного △АВС. При помощи подобия треугольников нетрудно определить в каком отношении проекции точек K, L и М поделят радиусы описанной окружности основания.

Подсказка 2

Рассмотрите центр основания и треугольники, полученные соединением этой точки с вершинами треугольника-проекции. Возможно, получится узнать их площади как части площадей треугольников полученных соединением центра основания с вершинами △ABC. Так мы узнаем площадь проекции!

Подсказка 3

Теорема косинусов поможет нам узнать стороны исходной фигуры-сечения. А уж искать площадь треугольника с известными сторонами мы умеем множеством способов! Осталось применить теорему о площади ортогональной проекции и задача убита.

Показать ответ и решение

Примем сторону тетраэдра за $a.$ Угол будем искать через косинус, который равен отношению площади $S 1$ треугольника $K L M − 1 1 1$ проекции треугольника $KLM$ на плоскость основания, к площади $S2$ самого треугольника $KLM$ - сечения.

$PIC$

Площадь проекции $S1$ определяется несложно, так как вершины $K1,L1,M1−$ делят соответствующие радиусы описанной окружности основания (площадь основания $√- S0 =-34 a2$ ) в тех же отношениях что и соответствующие им точки $K,L,M$ делят боковые стороны тетраэдра. Тогда площади треугольников $△K1OL1$ и $△COB,$ $△L1OM1$ и $△BOA,$ $△M1OK1$ и $△AOC$ с общим углом при вершине $O$ относятся, как произведение сторон.

( ) √- S = 1⋅S 1⋅ 2 + 1 ⋅ 2+ 1 ⋅ 1 =-5S = 5-3a2 1 3 0 4 3 2 3 4 2 24 0 96

Стороны сечения будем вычислять по теореме косинусов: $7- KL = 12a,$ $√13 LM = 6 a,$ $√3 MK = 4 a$ . Теперь вычислим площадь сечения. Косинус угла $α$ , лежащего напротив стороны $KL$ равен $-5-- cosα = √156-$ . Тогда $√131 sin α= √156$ . Для площади сечения получим следующий результат