Случаи расположения точек
Ошибка.
Попробуйте повторить позже
Длина ребра куба равна 1. Найдите радиус сферы, проходящей через точку
и касающейся прямых
и
.
Источники:
Подсказка 1
Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.
Подсказка 2
Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?
Подсказка 3
Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?
Подсказка 4
Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать
Введём декартову систему координат с центром в точке , ось абсцисс — луч
, ось ординат — луч
, ось аппликат — луч
.
Пусть — проекция центра сферы на грань
куба. Определим ее местоположение. Так как сфера касается прямых
и проходит через точку
, то расстояние от точки
до прямых
и
и точки
одинаково (обозначим его
).
Тогда
лежит на луче
, который является биссектрисой угла
. Осталось учесть условие, что центр сферы
касается прямой
, то есть нужно проверить, что расстояние от центра до прямой
совпадает с радиусом сферы
.
Заметим, что есть два случая расположения точки (на рисунке показаны разными цветами):
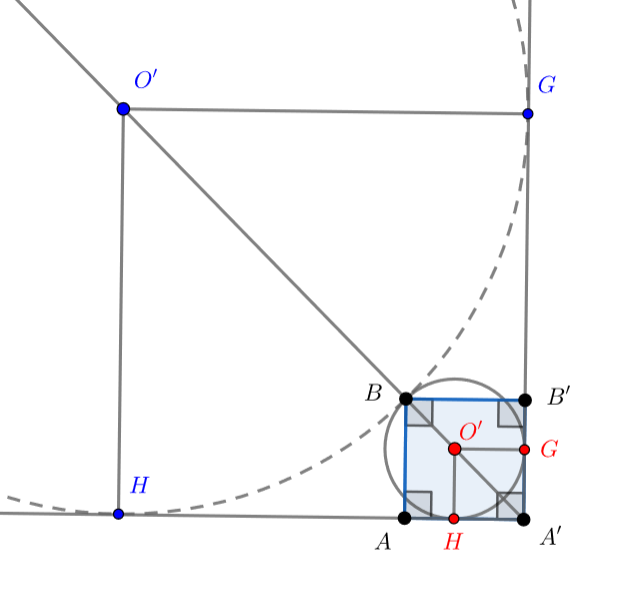
Случай 1: точка лежит на диагонали
.
Тогда из теоремы Пифагора для прямоугольного треугольника получим:
, откуда
. Значит,
центр сферы
имеет координаты
.
Расстояние до прямой равно
. То есть радиус
Случай 2: точка лежит на продолжении луча
.
Тогда из теоремы Пифагора для прямоугольного треугольника получим:
, откуда
. Значит,
центр сферы
в этом случае имеет координаты
.
Расстояние до прямой равно
. То есть радиус
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




