Тема Счёт отрезков в стерео

Случаи расположения точек

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт отрезков в стерео

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80774

В основании призмы лежит равносторонний треугольник площади 1. Площади её боковых граней равны 3, 3 и 2. Найдите объём призмы.

Источники: Физтех - 2024, 11.7 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, надо осознать картинку. Она, как будто, симметричная, но не стоит так думать сразу. Давайте опустим высоты из точки A_1 на прямые AB, AC, и плоскость ABC. Что тогда можно заметить? Какие принципиально разные случаи есть падения высоты на плоскость ABC?

Подсказка 2

Есть два случая - падение во внутрь призмы и во вне. Однако, при всем этом, у нас расстояния от точки A_1’(основание высоты) до прямых AB и AC равны, в силу равенства прямоугольных треугольников. Как тогда можно равносильно переформулировать случаи, когда высота падает во внутрь, а когда наружу? Как связать это с равноудаленностью от сторон?

Подсказка 3

Все верно, либо точка основания высоты лежит на внешней биссектрисе, либо на внутренней(угла BAC). Давайте посмотрим на второй случай. Мы видим, что прямые AA’ и A_1A’ перпендикулярны BC. Что тогда это значит? Чем это хорошо в нашей картинке?

Подсказка 4

Тем, что тогда BB_1 перпендикулярен BC, а значит BB_1C_1C - прямоугольник. Но тогда, если сторона треугольника в основании равна а, выходит, что a * AA_1 = 2, a * A_1K = 3. Тогда, пришли к противоречию, так как A_1K > AA_1. Значит, остался второй случай. Если прямая внутренней биссектрисы, была перпендикулярна прямой BC, то внешняя биссектриса будет…

Подсказка 5

Параллельна! А тогда, высота в параллелограмме CC_1B_1B - высота призмы. Значит, остается найти C_1H. Ну, а это уже чисто дело техники(и нескольких теорем Пифагора).

Показать ответ и решение

Если бы призма была прямая, то площади боковых граней были бы равны. Значит, призма наклонная.

Обозначим призму $ABCA1B1C1,$ площади из условия $SAA1B1B = SAA1C1C = 3.$

Пусть $A1K, A1M$ — высоты параллелограммов $AA1B1B$ и $AA1C1C.$ Тогда $A1K = A1M,$ т.к. площади равны, а также равны их основания, так как равносторонний треугольник.

Пусть $′ A$ — проекция $A1$ на плоскость $ABC.$ Тогда $′ ′ A K = AM,$ следовательно, точка равноудалена от прямых $AB$ и $AC.$

(a) Рассмотрим случай, когда $′ A$ принадлежит биссектрисе $AL$ угла $∠ABC.$ $AL$ — высота, медиана и биссектриса в равностороннем треугольнике.

$PIC$

AL ⊥ BC } ′ A1A′ ⊥ BC =⇒ BC ⊥(AA1A ) =⇒ BC ⊥ AA1 =⇒ BC ⊥ BB1

Тогда получаем, что $BB1C1C$ — прямоугольник. Пусть сторона треугольника $ABC$ равна $a.$ Посчитаем площадь прямоугольника и параллелограмма.

S1 =a ⋅AA1, S2 = a⋅A1K

2 =a ⋅AA1, 3= a⋅A1K

Но $A1K < AA1,$ тогда

3= a⋅A1K < a⋅AA1 = 2

получаем противоречие.

(b) Рассмотрим случай, когда $A′$ принадлежит внешней биссектрисе $AL$ угла $∠ABC.$

$PIC$

AA′ ∥BC )|} A1A∥BB1 =⇒ (AA1A′) ∥(BB1C ) AA′ ∥BC |)

Но $(AA1A′)⊥(ABC ),$ следовательно, $(BB1C)⊥ (ABC ),$ откуда следует, что высота $CH1$ параллелограмма $CC1B1B$ совпадает с высотой призмы $(C1H = A1A′).$ В итоге

V = SABC ⋅CH1 = 4√3

Ответ:

$√43-$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#81377

Длина ребра куба $ABCDA ′B′C′D′$ равна 1. Найдите радиус сферы, проходящей через точку $B$ и касающейся прямых $AD,AA′$ и $′ ′ A B$ .

Источники: Миссия выполнима - 2024, 11.4 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.

Подсказка 2

Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?

Подсказка 3

Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?

Подсказка 4

Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать

Показать ответ и решение

Введём декартову систему координат с центром в точке $A$ , ось абсцисс — луч $AD$ , ось ординат — луч $AA ′$ , ось аппликат — луч $AB$ .

Пусть $′ O$ — проекция центра сферы на грань $′ ′ AA B B$ куба. Определим ее местоположение. Так как сфера касается прямых $′ ′′ AA ,A B$ и проходит через точку $B$ , то расстояние от точки $′ O$ до прямых $′ AA$ и $′ ′ A B$ и точки $B$ одинаково (обозначим его $r$ ). Тогда $′ O$ лежит на луче $′ A B$ , который является биссектрисой угла $′ ′ AA B$ . Осталось учесть условие, что центр сферы касается прямой $AD$ , то есть нужно проверить, что расстояние от центра до прямой $AD$ совпадает с радиусом сферы $OB$ .

Заметим, что есть два случая расположения точки $′ O$ (на рисунке показаны разными цветами):

$PIC$

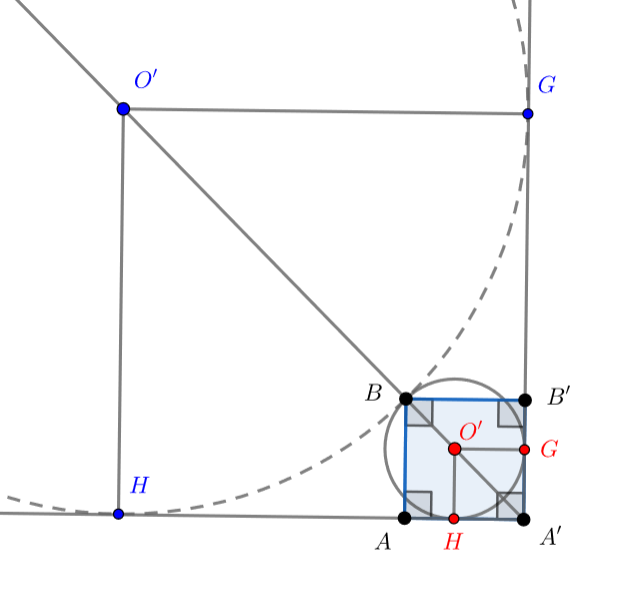
Случай 1: точка $O ′$ лежит на диагонали $A ′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-− r)2$ , откуда $r =2− √2$ . Значит, центр сферы $O$ имеет координаты $(x1;√2-− 1;2− √2)$ .

Расстояние до прямой $AD$ равно $∘(√2−-1)2-+(2−-√2)2$ . То есть радиус $OB = ∘(√2-− 1)2+(2−-√2)2 = ∘9−-6√2.$

Случай 2: точка $O ′$ лежит на продолжении луча $A′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-+r)2$ , откуда $r =2+ √2$ . Значит, центр сферы $O$ в этом случае имеет координаты $(x ;−√2-− 1;2+ √2) 2$ .

Расстояние до прямой $AD$ равно $∘--√-----2-----√--2 (− 2− 1) + (2+ 2)$ . То есть радиус $∘ --√----2-----√--2- ∘ ---√-- OB = (− 2− 1)+ (2+ 2) = 9+6 2.$

Ответ:

$∘9-±-6√2$

Ошибка.
Попробуйте повторить позже

Задача 3#63888

$ABCD$ — правильная пирамида, в основании которой лежит правильный треугольник $ABC$ со стороной 2. Боковые ребра пирамиды равны 3. Найдите площадь равнобедренного треугольника, одна вершина которого совпадает с $A$ , другая — с серединой $CD$ , а третья лежит на отрезке $BC.$

Показать ответ и решение

Обозначим искомый треугольник $AMN, M$ — середина $CD,N$ на $BC$ . Пусть $T$ — середина $AB$ , тогда $MT$ — высота треугольника. Если $′ M$ — проекция $M$ на высоту $CT$ треугольника $ABC$ , то по теореме Фалеса $′ CM$ равна половине $CO$ , где $O$ — проекция $D$ и одновременно центр описанной окружности (потому что боковые рёбра пирамиды равны), то есть равна половине радиуса описанной около ABC окружности. По теореме синусов $∘ √- R = 2∕(2⋅sin60 )= 2∕ 3$ , тогда

$′ ′ ∘ R- 2- TM = CT − CM = 2sin60 − 2 = √3$ , а

$√------ √-- MM ′ = DO2-=-CD22−R2-= 2√233-$ ,

тем самым $TM = √M-′T2+-M′M2 = ∘23+-4 =∘ 39= √13 12 3 12 2$

Поскольку $AT = AB∕2= 1$ , $AB ⊥(CTD ),$ то по теореме Пифагора

∘---2----2 ∘ 13--- √17- AM = TM + AT = 4 + 1= 2

Возможны случаи:

1) $AM = MN$ . В этом случае $N$ совпадает с $B$ , поскольку пирамида симметрична относительно плоскости, проходящей через середину $CD$ и перпендикулярной $AB$ . Тогда $√-- SAMN = 12 ⋅AB ⋅MT = MT = -123$

2) $AM = AN$ . Но тогда $√ -- AN =-217 >2 =AB = AC$ . Но тогда точка $N$ лежит вне отрезка $BC$ , иначе расстояние от $A$ до неё было бы не больше длины стороны треугольника $ABC$ .

3) $AN =MN$ . Заметим, что $cos∠BCD = BCC∕D2= 13$ . Пусть $CN = x,NB = 2− x$ , запишем теоремы косинусов для $△MCN$ и $△ABN$ , выберем из первого $MN$ , а из второго $AN$ в качестве противолежащих сторон, откуда

AN2 = (2 − x)2+22− 2⋅2(2 − x)⋅ 1 =MN2 =x2 + 9 − 2 ⋅ 3x⋅ 1=⇒ x= 7 2 4 2 3 4

Подставляя $x$ в теорему косинусов, получаем $MN2 = 4196 + 94 − 74 = 5716$ . Посчитаем высоту $h$ из вершины $N$ в треугольнике $ANM$ с учётом $AN = NM$

∘ ------- ∘-- √-- h= ∘NM2--− (AM-∕2)2 = 57− 17= 5= -10 16 16 2 2

Тогда $1 1 √17- √10 √170- SAMN = 2 ⋅h⋅AM = 2 ⋅ 2 ⋅ 2 = 8 .$

Ответ:

$√170 8$ или $√13 2$

Ошибка.
Попробуйте повторить позже

Задача 4#33366

Рассмотрим всевозможные тетраэдры $ABCD$ , в которых $AB = 2,AC =CB = 5,AD =$ $DB =6$ . Каждый такой тетраэдр впишем в цилиндр так, чтобы все вершины оказались на его боковой поверхности, причём ребро $CD$ было параллельно оси цилиндра. Выберем тетраэдр, для которого радиус цилиндра - наименьший из полученных. Какие значения может принимать длина $CD$ в таком тетраэдре?

Источники: Физтех - 2021, 11.2 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем, а как использовать равные отрезки? В каких треугольниках они состоят, что можно отметить в таких фигурах?

Подсказка 2

Отметим E — середину AB в равнобедренных треугольниках ADB и ACB! Какие тогда выводы можно сделать об AB?

Подсказка 3

AB — хорда окружности, перпендикулярной оси цилиндра. Давайте теперь подумаем, а в каких случаях мы смогли бы уменьшить радиус цилиндра?…

Подсказка 4

Мы можем уменьшать радиус цилиндра, если AB не является диаметром указанной окружности. Какие тогда выводы можно сделать из условия на минимальность радиуса цилиндра?

Подсказка 5

Мы должны рассматривать такие тетраэдры, в которых AB является диаметром цилиндра! Давайте теперь попробуем воспользоваться тем, что CD перпендикулярен основанию цилиндра. Что полезного можно отметить?

Подсказка 6

Отметим H — проекцию точек C и D на основание цилиндра! Осталось лишь воспользоваться тем, AB — диаметр, и немного посчитать ;)

Показать ответ и решение

Пусть $E$ — середина $AB.CE$ и $DE$ — медианы равнобедренных треугольников $ABC$ и $ABD$ , a значит, биссектрисы и высоты. То есть $AB ⊥ CE,AB ⊥ DE$ . Значит, отрезок $AB$ перпендикулярен плоскости $CDE$ , следовательно, $AB ⊥ CD$ .

$PIC$

Таким образом, $AB$ лежит в плоскости, перпендикулярной оси цилиндра (обозначим эту плоскость через $α$ ). Сечение цилиндра этой плоскостью — окружность, а $AB$ является хордой этой окружности. Тогда радиус цилиндра минимален, если $AB−$ диаметр. Отметим, что это возможно в силу того, что отрезки $DE$ и $CE$ длиннее, чем $12AB =1$ . Действительно, из треугольников $ACE$ и $ADE$ следует, что

CE = ∘52-− 12 = 2√6,DE = ∘62−-12 = √35

Рассмотрим тетраэдр, в котором $AB$ является диаметром цилиндра. Возможны 2 случая: точки $C$ и $D$ лежат по одну (этот случай представлен выше) или по разные стороны плоскости $α$ .

Пусть $H$ - проекция точек $C$ и $D$ на плоскость $α$ . Угол $∠AHB =90∘$ , так как он вписан в окружность и опирается на её диаметр. $AH = BH$ в силу равенства треугольников $ACH$ и $BCH$ . Тогда $AH =$ $√- BH = 2$ . По теореме Пифагора в прямоугольных треугольниках $AHC$ и $DHC$ соответственно: $CH =$ $-- -- √25− 2-=√ 23,DH = √36−-2= √34$ .

Тогда, если точки $C$ и $D$ лежат по одну сторону от плоскости $α$ , то $CD =DH − CH = √34− √23$ . Если точки $C$ и $D$ лежат по разные стороны от плоскости $α$ , то $CD = DH + CH = √34+√23-$ .

Ответ:

$√34-±√23$

Критерии оценки

Доказано, что 𝐴𝐵 – диаметр цилиндра наименьшего радиуса – 2 балла; если при этом не проверено, что точки 𝐶 и 𝐷 могут лежать на боковой поверхности такого цилиндра (например, можно доказать, что треугольники 𝐴𝐵𝐶 и 𝐴𝐵𝐷 остроугольные; можно сделать, как в решении), то 1 балл вместо 2;

найдены оба значения 𝐶𝐷 – 3 балла;

найдено только одно значение 𝐶𝐷 – 1 балл вместо 3.

Ошибка.
Попробуйте повторить позже

Задача 5#63894

В основании пирамиды $SABC$ лежит треугольник $ABC$ со сторонами $AB = BC = 3√2-$ и $AC =2√6$ . Высота пирамиды равна $√ - 6$ и видна из вершин $A$ и $C$ под одним и тем же углом, равным $√1 arcsin 3$ . Под каким углом она видна из вершины $B?$

Источники: ПВГ-2019, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Пусть SH – высота пирамиды, подумайте, на каком значимом отрезке в треугольнике лежит точка Н?

Подсказка 2

Она лежит на медиане, биссектрисе и высоте треугольника △АВС! Тогда мы без труда сможем выразить ВН через стороны треугольника и данные/интересующие нас уголочки (только не забудьте рассмотреть два случая: ведь точка Н может лежать как внутри, так и вне треугольника △АВС), откуда мы и можем найти тригонометрическую функцию искомого угла

Показать ответ и решение

Поскольку высота $SH$ пирамиды видна из вершин $A$ и $C$ под одним и тем же углом, точка $H$ лежит на медиане (она же биссектриса и высота) $BM$ треугольника $ABC$ или её продолжении.

$PIC$

Если $SH =h,AB = BC =a$ , $AC = b$ и $∠SAH = ∠SCH = α$ , а искомый угол $∠SBH = β$ , то имеем

∘------ ∘ ----------- BH = hctgβ =BM ±MH = a2− b2± h2 ctg2α− b2, 4 4

откуда, подставляя данные задачи, получаем $√- ctgβ = 2± 1$ , в зависимости от того, лежит ли точка $H$ внутри треугольника $ABC$ или вне него. Значит, $π β = 8$ или $3π β = 8 .$

Ответ:

$π∕8$ или $3π∕8$

Ошибка.
Попробуйте повторить позже

Задача 6#69439

Рассматриваются плоские сечения правильной пирамиды $SABCD$ , параллельные боковому ребру $SB$ и диагонали основания $AC$ , в которые можно вписать окружность. Какие значения может принимать радиус этих окружностей, если $AC = 1$ , $2 cos∠SBD = 3?$

Источники: ПВГ-2010, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

В этой задаче условие может выглядеть очнеь страшно, поэтому первым делом нужно нарисовать аккуратный чертеж, чтобы понять, с какими объектами мы работаем. Теперь давайте подумаем, нам дана правильная пирамида (какой вывод можно сделать про ее основание?), мы знаем сторону и один из углов. Попробуем найти длины полезных отрезков в этой пирамиде. Например, с помощью косинуса SBD и длины OB (O - центр основания) можно найти SB - боковое ребро пирамиды!

Подсказка 2

Итак, вспомним, что это можно сделать, опустив высоту из S и заметив, что SOB - прямоугольный треугольник с известным нам катетом и углом. Итак, мы нашли длину боковой стороны, а теперь подумаем про сечения. Если вы нарисовали чертеж - подумайте, какие вообще варианты сечений у нас могут получаться? (вряд ли сечением пирамиды будет двенадцатиугольник, например). Затем попробуем рассмотреть каждый вид сечений отдельно.

Подсказка 3

Верно! У нас могут быть сечения всего двух видов - пятиугольные и треугольные! Мы знаем, что наше сечение пересекает плоскость основания по прямой A₁C₁, параллельной прямой AC. Обозначим за O- центр ABCD. Какое будет сечение, если прямая A₁C₁ лежит внутри треугольника ADC?

Подсказка 4

Верно! Это будет треугольник. Пускай S₁- его вершина, лежащая на ребре SD, а x- длина A₁C₁. Попробуйте найти S₁B₁ (выразить через х), где B₁- точка пересечения A₁C₁ и BD, если вы знаете, что S₁B₁ параллельна SB...

Подсказка 5

Площадь сечения должно получиться S₁B₁⋅A₁C₁/2=3x²/16. S₁C₁ можно найти из теоремы Пифагора. Воспользуйтесь тем, что r=S/p для оценки радиуса. А какое сечение будет, если A₁C₁ лежит внутри треугольника ACB?

Подсказка 6

Домик). Переобозначим A₁C₁ за A₂C₂=x, A₃- точка пересечения сечения и AS, C₃- сечения и SC, Q- сечения и SD, B₃- сечения и BD. Из того, что A₂A₃ и C₂C₃ параллельны SB и A₂C₂ и A₃C₃ параллельны AC, можно получить, что A₂A₃C₃C₂- параллелограмм, а т.к. SB перпендикулярен AC- прямоугольник. Попробуйте найти отрезки A₂A₃ и QA₃...

Подсказка 7

Если в наш пятиугольник можно вписать окружность, то будет верна формула S=pr. При этом мы знаем, что r=x/2, ведь наша окружность касается параллельных прямых A₂A₃ и C₂C₃, расстояние между которыми равно x. Осталось только посчитать площадь и полупериметр, и решить уравнение S=px/2

Показать ответ и решение

Так как пирамида правильная, то в основании лежит квадрат с диагоналями $AC =BD = 1$ , пусть $O$ — его центр. Тогда $SO$ является высотой пирамиды, так что из условия про косинус находим

2 OB 0,5 3 =cos∠SBD = SB-= SB-

3 SB = 4

Плоскость сечения параллельна $SB$ , поэтому содержит параллельную $SB$ прямую из плоскости $SBD$ . Поэтому сечение может быть двух видов:

$PIC$

1 случай) треугольник $A1S1C1$ , где $A1C1$ лежит внутри $△ADC$ .

Тогда $0<A1C1 < 1$ (строго меньше единицы, потому что сечение параллельно $AC$ , содержать $AC$ не может). Пусть $x A1C1 =x =⇒ A1B1 = B1C1 = 2$ .

∘ x ∠A1DB1 =∠DA1B1 = 45 =⇒ DB1 = 2

△DS1B1 ∼ △DSB =⇒ S1B1= DB1- =⇒ SB DB

=⇒ S1B1 = x2- =⇒ S1B1 = 3x 34 1 8

Теперь найдём, чему равняется $O1B1$ (то есть радиус вписанной окружности)

$PIC$

∘ -------- x2 9x2 5x S1C1 = 4-+ 64-= 8-

sin(∠O1S1H)= O1H- =-3xr-- = O1S1 8 − r

x ( ) =-25x- =⇒ r = x =⇒ r ∈ 0;1 8 6 6

2 случай) Пятиугольное сечение плоскостью $A C C 2 2 3$ , где $A C 22$ лежит внутри $△ABC$ . Заметим, что $A C || A C 2 2 3 3$ и $A C = A C , 2 2 3 3$ поэтому $A A || C C 2 3 3 2$ и $A A = C C . 2 3 3 2$