.18 Статика. Условия равновесия тела
Ошибка.
Попробуйте повторить позже
Тонкий однородный массивный стержень массой и длиной
подвешен на двух невесомых нерастяжимых нитях
длиной
и
которые прикреплены к концам стержня и к одной точке горизонтального потолка (см. рисунок). Найти
силы натяжения нитей.
(«Росатом», 2022, 11)
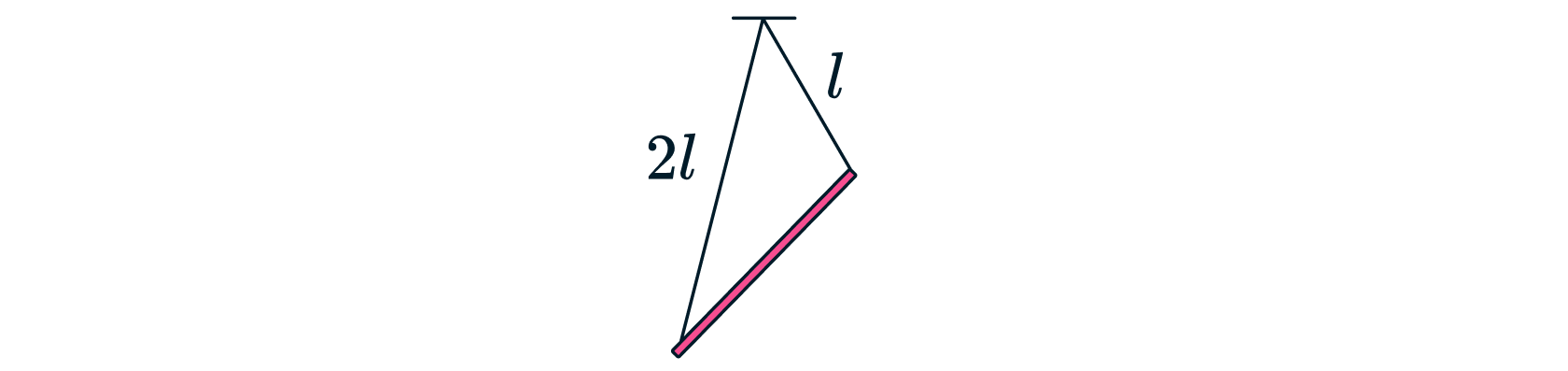
Источники:
На стержень действуют сила тяжести и силы натяжения со стороны нитей, обозначим силы и углы между нитями и стержнем на рисунке:
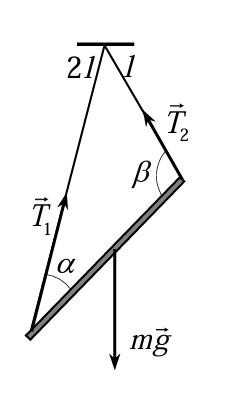
Поскольку стержень однородный сила тяжести приложена к центру стержня. Стержень покоится, запишем условие равенства нулю суммы моментов сил, действующих на стержень, ось вращения возьмем в центре стержня, положительными будет считать моменты, вращающие стержень по часовой стрелке:
Отсюда:
Запишем теорему синусов для треугольника, образованного нитями и стержнем:
Поделив одно уравнение на другое, получим:
где – некоторый коэффициент пропорциональности между силой натяжения и длиной нити, одинаковый для обеих
нитей.
Тогда силы натяжения:
Запишем условие равентсва нулю векторной суммы сил, действующих на стержень:
Изобразим векторный треугольник, образованный силами:
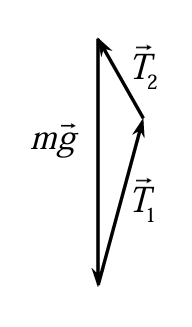
В этом треугольнике угол между векторами и
равен
. Запишем теорему косинусов для этого
треугольника:
Подставим выражения для сил натяжения:
Запишем теорему косинусов треугольника, образованного нитями и стержнем:
Отсюда:
Подставляя в теорему косинусов для векторного треугольника, получим:
Тогда силы натяжения равны:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




