.18 Статика. Условия равновесия тела
Ошибка.
Попробуйте повторить позже
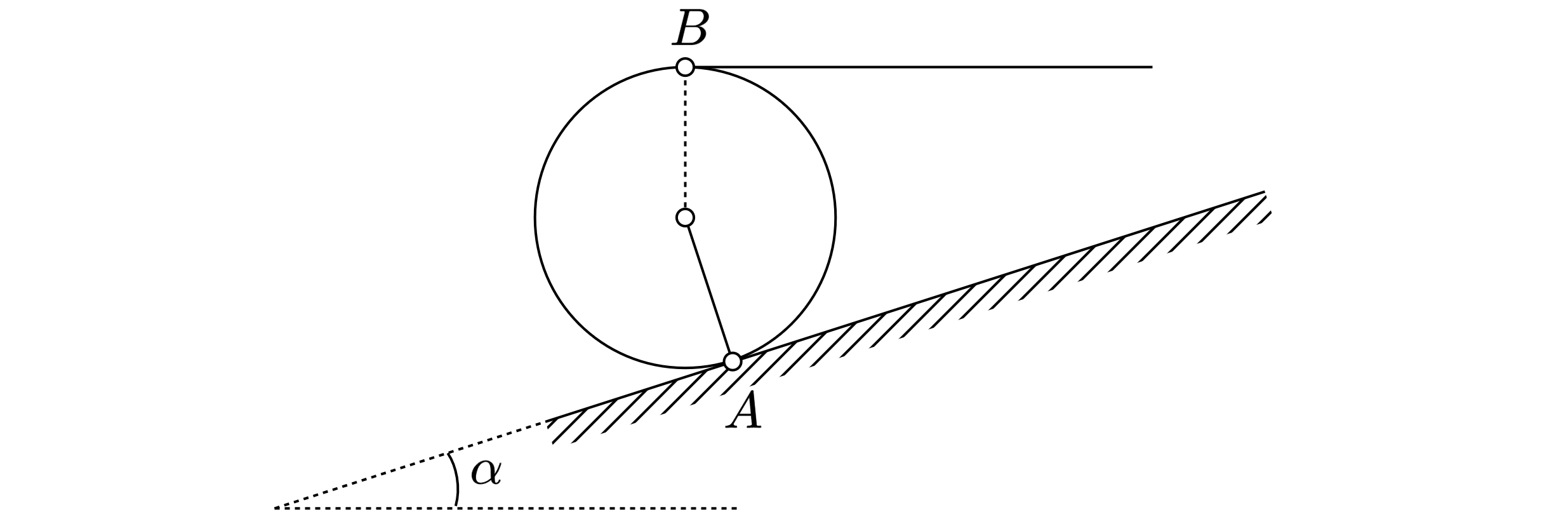
Однородный шар радиусом 
и массой 
удерживается на наклонной плоскости горизонтальной нитью, прикреплённой
к нему в точке B. Найти натяжение нити 
и коэффициент трения 
в точке A, если угол наклона плоскости к
горизонту равен 
.
(МОШ, 2019, 11)
Источники:
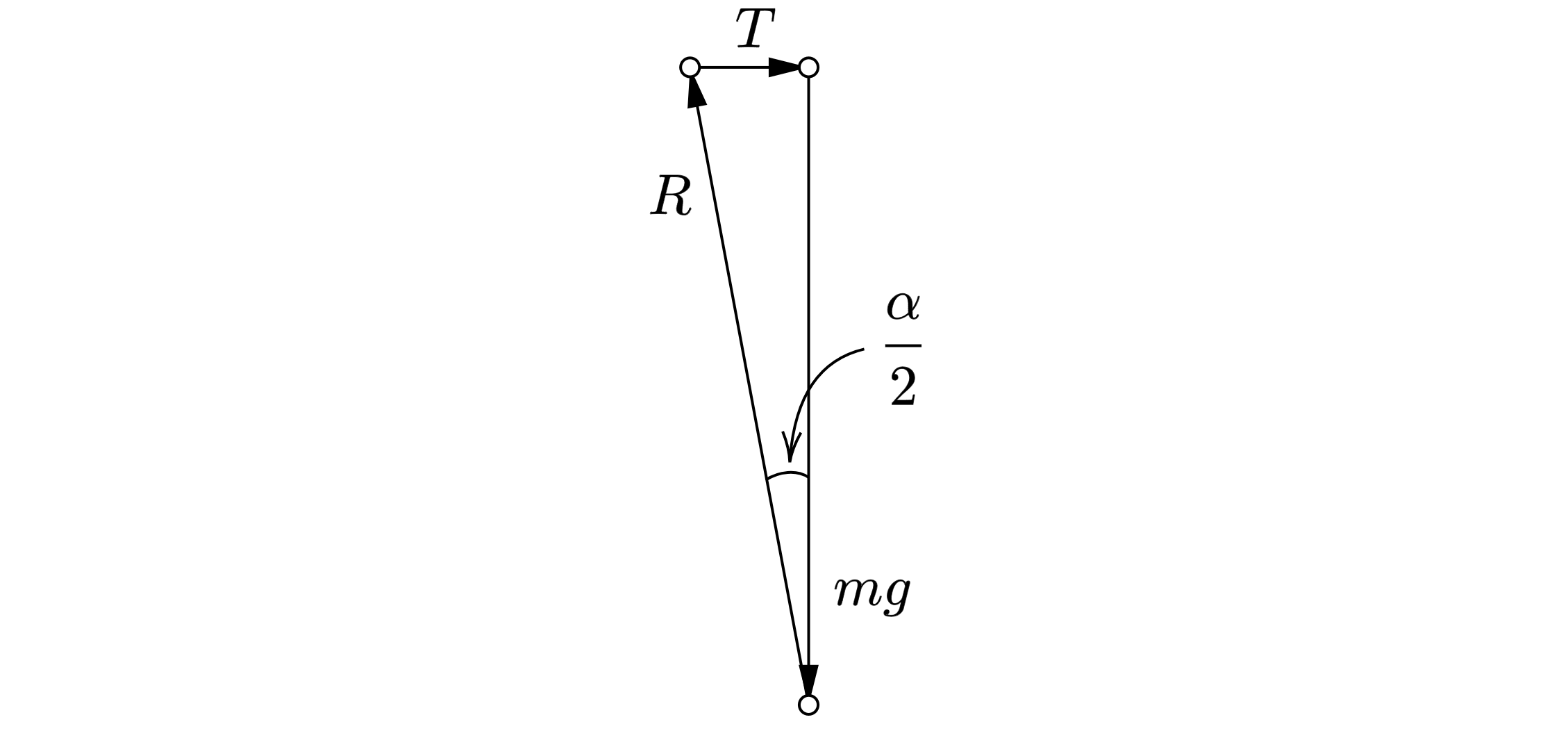
Так как шар покоится под действием плоской системы трёх непараллельных сил (сила тяжести, сила реакции со
стороны опоры 
и сила реакции со стороны нити 
), следовательно, линии действия этих сил пересекаются в одной
точке. Значит, линия действия силы 
должна пройти через точку пересечения 
и 
, отклоняясь от нормали на
угол 
. Равновесие шара возможно, если угол 
, где 
– угол трения (максимальный угол, на который
может отклониться от нормали вектор силы реакции). Стало быть, 
Величину 
находим из силового
треугольника для шара:
(Официальное решение МОШ)
| Критерии оценивания выполнения задачи | Баллы |
| Линии действия трёх сил пересекаются в одной точке | 2 |
| Линия действия силы | 2 |
|
| 2 |
| Нарисован силовой треугольник | 2 |
| Представлен правильный ответ (численный и в общем виде) | 2 |
| Максимальный балл | 10 |
отклоняется от нормали на угол 
(ответ в общем виде и численное значение) 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
