.18 Статика. Условия равновесия тела
Ошибка.
Попробуйте повторить позже
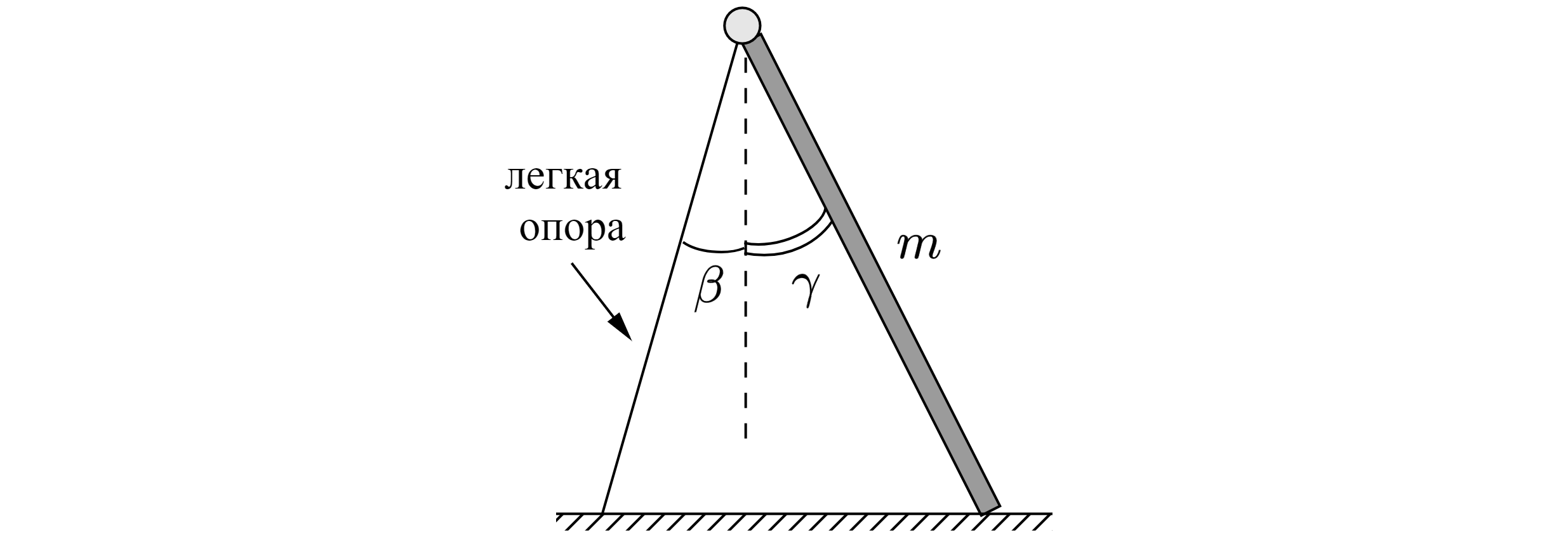
На рисунке изображена упрощённая модель лестницы-стремянки, состоящей из соединённых шарнирно легкой опоры
и массивной части, наклоненных под углами и
к вертикали (
). Масса лестницы
. Определите, с какой силой взаимодействуют между собой части лестницы. Трения в шарнире нет.
Коэффициент трения между полом и касающимися его частями стремянки одинаков. При каком минимальном
значении коэффициента µ части лестницы не будут разъезжаться? Ускорение свободного падения
.
(Всеросс., 2019, финал, 9)
Источники:
Рассмотрим внешние силы, действующие на всю лестницу (рис. 1). Из правила моментов относительно правой
нижней точки, с учетом соотношения , получим
. Откуда
, а

Сила, действующая на опору со стороны шарнира может быть направлена только вдоль нее (рис. 2). В противном случае возникнет некомпенсированный момент относительно нижней точки опоры. Таким образом
Из равенства нулю суммы горизонтальных сил следует, что силы трения равны. Но, первой проскользнет легкая опора, так как на нее действует меньшая сила нормальной реакции. Минимальное значение коэффициента трения:
(Официальное решение ВсОШ)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




