Школьный 8 - 9 класс
Ошибка.
Попробуйте повторить позже
На шахматной доске стоял король. Каждый из королей находился под боем хотя бы одного из остальных. После того как
несколько королей убрали, никакие два из оставшихся королей друг друга не бьют. Какое наибольшее число королей могло
остаться?
Источники:
Подсказка 1
Попробуйте оценить, сколько снятый король бил королей, которые остались на доске.
Подсказка 2
Верно! Он бил максимум 4 короля. Попробуйте оценить количество королей, которые остались через количество снятых королей.
Подсказка 3
Правильно! Королей которые остались не более, чем в 4 раза больше, чем количество снятых. Теперь попробуйте оценить количество оставшихся королей числом, зная, что 21 - количество снятых = количеству оставшихся.
Подсказка 4
Верно! Количество оставшихся не более 16. Осталось только привести пример.
Заметим, что каждый король, снятый с доски, мог бить не более из оставшихся (иначе и некоторые из оставшихся били бы друг друга).
Поэтому число оставшихся королей не может превосходить число снятых более чем в
раза, то есть не может быть больше
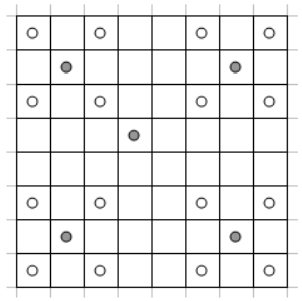
Пример
приведён на рисунке: серым обозначены короли, которых необходимо убрать.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




