Поиск объёмов или решение через вспомогательные объёмы
Ошибка.
Попробуйте повторить позже
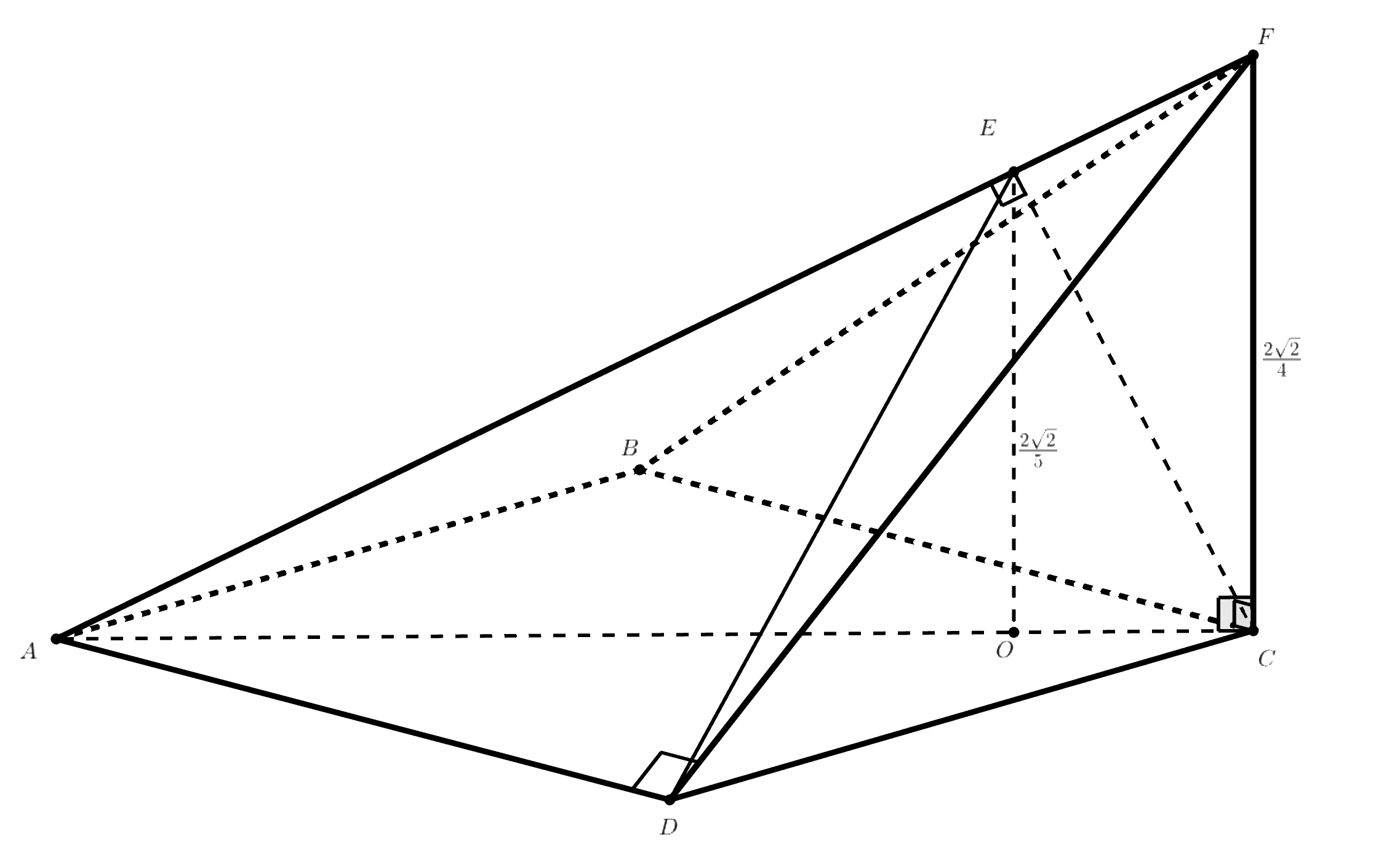
Основанием четырёхугольной пирамиды является квадрат
На ребре
взята точка
такая, что отрезок
перпендикулярен ребру
Проекция
точки
на основание пирамиды лежит на отрезке
и делит его в
отношении
Найти разность объёмов пирамид
и
если известно, что
а
Знаем, что и
тогда и только тогда, когда
Так как
то
Заметим, что так как
перпендикулярна плоскости основания пирамиды, и
так как диагонали квадрата
перпендикулярны. Таким образом,
в частности,
То есть
перпендикулярна двум пересекающимся прямым в
плоскости
(
и
), а, значит,
— высота пирамиды.
Найдём значения отрезков:
Так как — высота треугольника
, опущенная из прямого угла,
Рассмотрим и
Они подобны по двум углам — общему углу
и прямым углам
и
Запишем
отношение подобия:
Теперь вычислим объёмы интересующих нас пирамид:
Вычислим искомую как разность объёмов:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




