Поиск объёмов или решение через вспомогательные объёмы
Ошибка.
Попробуйте повторить позже
Дан куб со стороной 1, основаниями и боковыми рёбрами
и
. На рёбрах
отмечены точки
coответственно. Найдите отношение, в котором плоскость
делит объём куба, если известно,
что
и что
Подсказка 1
В условии нам дана сумма некоторых пар отрезков, быть может, тогда обозначим A’K за x и посчитаем остальные отрезки в грани ABB’A’? Также обратим внимание на то, что ребра в этой грани параллельны, так что можно использовать и подобие!
Подсказка 2
BL = 5/4 - x, LB’ = x - 1/4, а если провести AL до пересечения с A’B’ в точке T, то несложно выразить и B’T. А в составе какого отрезка лежит B’T? Давайте выразим его через больший треугольник!
Подсказка 3
B’T = A’T - 1, а A’T можно выразить через тангенс угла A! Теперь мы умеем выражать B’T двумя способами, чему тогда равен х?
Подсказка 4
x = 1/2! Супер, теперь мы знаем, что K — середина A’B’. Но ведь это верно не только для точки K…
Подсказка 5
Аналогично M — середина BC, O — середина DD’! Теперь мы видим, что сечение у нас достаточно красивое и даже симметричное ;) осталось понять, относительно чего…
Рассмотрим грань . Пусть
тогда
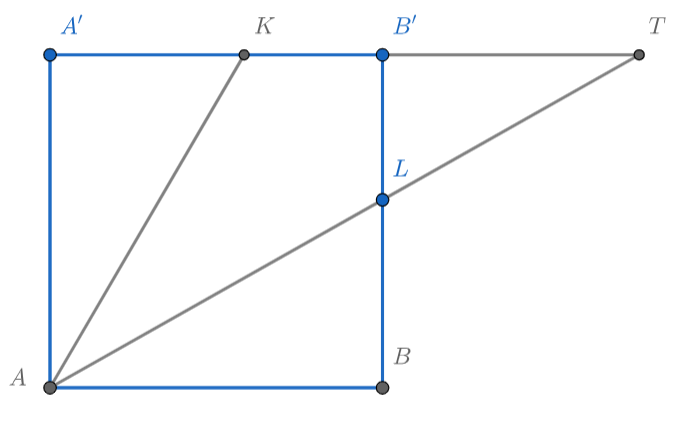
Продлим до пересечения лучи и
точку пересечения назовём
и выразим
, используя подобие треугольников
и
Выразим теперь вторым способом: через треугольник
и тангенс
Используя формулу тангенса двойного угла, получаем, что
Отсюда
Отсюда можно найти : перемножая пропорцию и приводя подобные, получим квадратное уравнение
, которое имеет
решения
и
По построению
не может превосходить единицу, поэтому
то есть
— середина
.
Аналогично получаем, что — середина
и
— середина
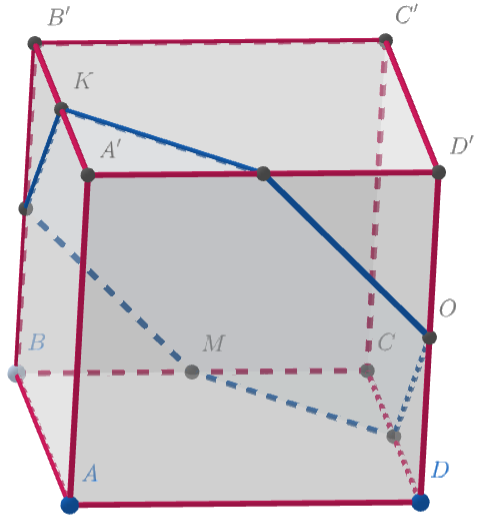
Заметим, что через проходит плоскость, которая высекает из данного куба шестиугольник и пересекает ещё три
ребра в серединах: рёбра
и
. Такая плоскость часто встречается в задачах: явно построить сечение можно
классическим способом, параллельными переносами отрезков. А если уже встречались с таким построением, можно показать,
что все 6 точек действительно лежат в одной плоскости, используя параллельность диагоналям граней куба. Поскольку
через три точки
можно провести только одну плоскость, этот шестиугольник и будет сечением куба плоскостью
Сечение центрально симметрично относительно центра куба Середины отрезков
и
симметричны относительно центра, как
и середины отрезков
и
и
. Таким образом, имеем центральную симметрию всего построения относительно центра
куба, следовательно, плоскость делит куб на две равные фигуры.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




