Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Поиск объёмов или решение через вспомогательные объёмы

Тема Счёт площадей и объёмов

Поиск объёмов или решение через вспомогательные объёмы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт площадей и объёмов

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79606

Ортогональной проекцией правильной треугольной пирамиды на некоторую плоскость является параллелограмм с острым углом $60∘$ . Найдите объём пирамиды, если площадь её боковой поверхности равна 54.

Источники: ОММО - 2024, задача 8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Чтобы нормально работать с картинкой, рассмотрим две пары скрещивающихся рёбер пирамиды (например, AB, CD, BC, AD). Ведь их достаточно для построения проекции. Пирамида правильная, значит, на этих рёбрах удобно отметить их середины (например, точки M, N, Q, P соответственно). Ведь отрезки MN и PQ являются перпендикулярами к этим рёбрам. Но, кажется, этого мало, ведь надо понять, какие свойства имеют их проекции. Попробуйте выяснить, как связаны эти отрезки и их проекции, основываясь на том, что ортогональная проекция пирамиды - параллелограмм.

Подсказка 2

В силу того, что проекцией пирамиды является параллелограмм, эти отрезки параллельны плоскости проекции. Тогда проекции MN и PQ параллельны самим отрезкам, равны им и перпендикулярны сторонам ромба. Также, так как пирамида правильная, MN и PQ равны, а значит, и их проекции тоже. Что тогда мы можем сказать про этот параллелограмм?

Подсказка 3

Верно! Это же ромб! Ведь в нём высоты, проведённые к смежным сторонам, равны. Тогда, если введём угол между ребром основания пирамиды и плоскостью проекции и длину стороны основания и боковой стороны трапеции (например, через a и b), то сможем выразить стороны ромба через a, b и этот угол и получить уравнение, ведь эти стороны равны.

Подсказка 4

Теперь мы получили, что тангенс угла между ребром основания пирамиды и плоскостью проекции равен a/b. Отлично! Мы можем выразить и синус, и косинус этого угла через a/b, а значит, и сторону ромба мы можем выразить через a и b (для удобства можно заменить a/b на новую переменную). Но мы ещё никак не воспользовались тем условием, что угол ромба равен 60 градусам. Это нужно исправить, например, записав уравнение на синус этого угла, выразив его как отношение высоты ромба на его сторону. Если мы ещё и выразим высоту через a и b, то получится записать уравнение на a и b.

Подсказка 5

Мы ведь знаем, что проекция MN - это высота ромба. Тогда так как проекция равна MN, то и высота равна этому отрезку. А вот его уже легче искать. Это можно сделать, выразив площадь треугольника MDC двумя способами.

Подсказка 6

Подставив MN в уравнение, мы получили, что (a/b)^2 = 2. Осталось воспользоваться последним условием задачи про площадь боковой поверхности. Выразив её через a и b, мы получаем уравнение, через которое находим a и b. Дело за малым, осталось лишь посчитать объём. И победа!

Показать ответ и решение

Пусть сторона основания пирамиды $DABC$ с вершиной $D$ равна $a$ , а боковое ребро равно $b$ . Для построения проекции достаточно рассмотреть две пары скрещивающихся ребер, например, $AB, CD,BC$ и $AD$ , проекции которых являются сторонами параллелограмма $A1B1C1D1.$

$PIC$

Пусть $MN$ — общий перпендикуляр пары рёбер $AB$ и $CD$ , а $PQ$ — общий перпендикуляр скрещивающихся рёбер $AD$ и $BC.$ Плоскость проекции $Ω$ параллельна как $MN$ , так и $P Q$ , поскольку ортогональной проекцией пирамиды является параллелограмм. Отрезки $MN$ и $PQ$ проектируются на плоскость $Ω$ без изменения длины в высоты параллелограмма $M1N1$ и $P1Q1$ , так как $ABB1A1$ и $DCC1D1$ обе перпендикулярны $Ω$ и будут параллельны друг другу, т.к. $A1B1C1D1$ — параллелограмм. То есть $MN$ не просто общий перпендикуляр $AB$ и $CD$ , но и общий перпендикуляр двух вышеописанных плоскостей. А значит, ещё это и общий перпендикуляр для $A1B1$ и $C1D1.$

Поскольку пирамида правильная, $MN = PQ$ . Следовательно, $M1N1 = P1Q1.$

В параллелограмме $A1B1C1D1$ высоты, проведённые к смежным сторонам, равны. Значит, параллелограмм является ромбом.

Пусть ребро $AB$ наклонено к плоскости $Ω$ под углом $α$ , тогда ребро $CD$ , которое перпендикулярно $AB$ , наклонено под углом $90∘− α.$ Отсюда $acosα= bsinα.$

$PIC$

Обозначим $ab = λ$ . Тогда $tgα= λ,A1B1 = acosα = √1a+λ2$ .

Найдём расстояние между скрещивающимися рёбрами правильной треугольной пирамиды как высоту сечения $DMC$ :

∘ ------ a√3- 2 a2 MC ⋅H = b⋅MN, 2 ⋅ b − 3 = b⋅MN

откуда

∘------ ∘----- MN = a2b 3b2− a2 = a2 3− λ2

Тогда синус острого угла пирамиды равен $sinφ = MA11ND11 = AM1NB1$ . Подставляя найденные выражения и данное в условии значение $φ =60∘$ , получим $- √32 = 12√3-−-λ2√1-+λ2-$ , откуда $λ= 0$ (что невозможно) или $λ2 =2.$

Площадь боковой поверхности пирамиды равна

∘ ----2- 2 √----2 S = 3a b2− a-= 3a-⋅-4−-λ- 2 4 4 λ

Подставив $S = 54$ и $λ= √2$ , найдём

a2 =72,b2 = a2= 36 λ2

Объём правильной пирамиды равен

a2∘ --2--2 √------- V = 12 3b − a = 6 108− 72=36

Ответ: 36

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#92263

Дан куб со стороной 1, основаниями $ABCD, A′B ′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′$ и $DD′$ . На рёбрах $A′B′,B ′B,BC,CD, DD′,D′A′$ отмечены точки $K,L,M,N,O,P$ coответственно. Найдите отношение, в котором плоскость $KMO$ делит объём куба, если известно, что

′ ∠A AK = ∠LAK,∠BAM = ∠NAM, ∠DAO = ∠PAO

и что

′ ′ 5 A K+ LB = BM + ND = DO +PA = 4.

Подсказки к задаче

Подсказка 1

В условии нам дана сумма некоторых пар отрезков, быть может, тогда обозначим A’K за x и посчитаем остальные отрезки в грани ABB’A’? Также обратим внимание на то, что ребра в этой грани параллельны, так что можно использовать и подобие!

Подсказка 2

BL = 5/4 - x, LB’ = x - 1/4, а если провести AL до пересечения с A’B’ в точке T, то несложно выразить и B’T. А в составе какого отрезка лежит B’T? Давайте выразим его через больший треугольник!

Подсказка 3

B’T = A’T - 1, а A’T можно выразить через тангенс угла A! Теперь мы умеем выражать B’T двумя способами, чему тогда равен х?

Подсказка 4

x = 1/2! Супер, теперь мы знаем, что K — середина A’B’. Но ведь это верно не только для точки K…

Подсказка 5

Аналогично M — середина BC, O — середина DD’! Теперь мы видим, что сечение у нас достаточно красивое и даже симметричное ;) осталось понять, относительно чего…

Показать ответ и решение

Рассмотрим грань $AA ′B ′B$ . Пусть $A ′K = x,$ тогда $BL = 5− x, 4$ $LB′ = x− 1. 4$

$PIC$

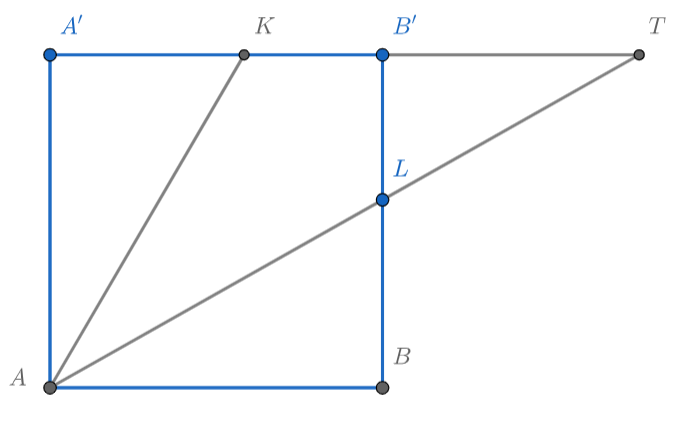
Продлим до пересечения лучи $AL$ и $A′K,$ точку пересечения назовём $T$ и выразим $B′T$ , используя подобие треугольников $ALB$ и $TLB ′ :$

B′T = x-− 14-= 4x−-1. 54 − x 5− 4x

Выразим теперь $′ B T$ вторым способом: через треугольник $′ AA T$ и тангенс $∠A :$

A′K tg∠A′AK = AA′-=x.

Используя формулу тангенса двойного угла, получаем, что

A′T = tg∠A ′AT = -2x-2. 1− x

Отсюда

′ ′ 2x−-1+-x2- 4x−-1 B T = A T − 1= 1− x2 = 5− 4x .

Отсюда можно найти $x$ : перемножая пропорцию и приводя подобные, получим квадратное уравнение $2 4x − 10x+ 4= 0$ , которое имеет решения $x =2$ и $1 x =2.$ По построению $x$ не может превосходить единицу, поэтому $1 x= 2,$ то есть $K$ — середина $′ ′ A B$ .

Аналогично получаем, что $M$ — середина $BC,$ и $O$ — середина $DD ′.$

$PIC$

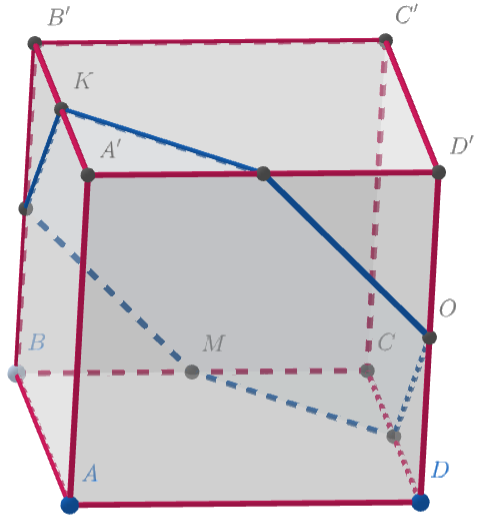
Заметим, что через $K,M,O$ проходит плоскость, которая высекает из данного куба шестиугольник и пересекает ещё три ребра в серединах: рёбра $A ′D ′,BB′$ и $CD$ . Такая плоскость часто встречается в задачах: явно построить сечение можно классическим способом, параллельными переносами отрезков. А если уже встречались с таким построением, можно показать, что все 6 точек действительно лежат в одной плоскости, используя параллельность диагоналям граней куба. Поскольку через три точки $K,M,O$ можно провести только одну плоскость, этот шестиугольник и будет сечением куба плоскостью $KMO.$

Сечение центрально симметрично относительно центра куба $I.$ Середины отрезков $CD$ и $B ′A′$ симметричны относительно центра, как и середины отрезков $A′D′$ и $BC,$ $DD ′$ и $B′B$ . Таким образом, имеем центральную симметрию всего построения относительно центра куба, следовательно, плоскость делит куб на две равные фигуры.

Ответ: 1 : 1

Ошибка.
Попробуйте повторить позже

Задача 3#92348

Все рёбра прямой треугольной призмы $ABCA ′B ′C′$ с основанием $ABC$ и боковыми ребрами $AA ′,$ $BB ′,$ $CC ′$ равны. Найдите отношение, в котором делит объем этой призмы плоскость, проходящая через вершину $′ C$ и через середины ребер $AB,$ $′ AA .$

Подсказки к задаче

Подсказка 1

Пусть M и N — середины AA’ и BB’ соответственно, секущая плоскость пересекает CB в точке K, а T — пересечение KN и TC’. Нам было бы очень полезно узнать, в каком соотношении K делит CB. Давайте тогда попробуем записать какие-нибудь подобия и отношения отрезков!

Показать ответ и решение

Пусть $M$ и $N$ — середины $AA′$ и $BB′$ соответственно. Пусть секущая плоскость пересекает отрезок $BC$ в точке $K$ и $′ C M ∩ KN = T$ (тогда наше сечение — это $′ KC MN$ ). Ясно, что $T$ лежит на прямой $AC.$ Пусть $AH$ — высота треугольника $ABC.$ Пусть $′ TH ⊥ BC,$ причем $′ H$ лежит на прямой $BC.$

$PIC$

$CC′$ и $AM$ параллельны, причем $AM = 12AA′ = 12CC ′,$ тогда треугольники $CC ′T$ и $AMT$ подобны с коэффициентом $2.$ Тогда $CT = 2AT.$ Треугольники $CAH$ и $TCH ′$ подобны с коэффициентом $2,$ так как $AH || TH ′$ и $TC = 2AC.$ Тогда $TH ′ =2AH.$ По теореме Менелая для треугольника $ABC$ и прямой $KN$ получаем

CK- ⋅ BN-⋅ AT-= 1 KB NA CT

Тогда получаем $CK-= 2, KB 1$ следовательно, $KB-= 1. BC 3$ Пусть $V =V ′′ ′. ABCA B C$ По формуле объема

′ 1 ′ V =SABCBB = 2AH ⋅BC ⋅BB

1 ′ 1 ′ 1 VABCC′ =3CC ⋅SABC = 6CC ⋅AH ⋅BC =3V

VCC′KT = VCC-′KT-⋅ V-= VCC′KT-V-= 4 V V∕3 3 VC′CBA 3 9

V = SANT-⋅ MA ⋅ V-= VAN-⋅AT-⋅sin∠NAT MNTA SABC AA′ 3 6CB ⋅CA ⋅sin∠CAB

Так как $∘ ∠CAB + ∠NAT = 180,$ то $sin∠CAB = sin∠NAT.$ Тогда $-V VMNTA = 12.$

Выразим объем фигуры $′ MC ANKC$ — одной из частей, на которые разделила призму секущая плоскость:

4 1 13 VMC ′ANKC =VCC′KT − VMNTA = 9V − 12V =36V

Тогда $VBKNA ′B′C′ = V − VMC ′ANKC = 2336V.$ Тогда получаем

23 VBKNA′B′C-′= 36V-= 23- VMC ′ANKC 1336V 13

Ответ: 13 : 23

Ошибка.
Попробуйте повторить позже

Задача 4#92367

Расстояние от середины высоты правильной четырёхугольной пирамиды до боковой грани равно $√2-$ , а до бокового ребра — $√3$ . Найдите объём пирамиды.

Показать ответ и решение

Пусть нам дана правильная четырехугольная пирамида $SABCD$ с основанием $ABCD.$ Пусть $O$ — основание высоты этой пирамиды. Заметим, что расстояние от $O$ до плоскости $BSC$ равно удвоенному расстоянию от середины высоты до этой плоскости. Аналогично с расстоянием до бокового ребра $AS.$ Пусть $OQ$ — перпендикуляр к $AS,$ а $OP$ — перпендикуляр к апофеме $SH$ плоскости $BSC.$

$PIC$

Так как $H$ — середина $BC,$ то $BC ⊥OH.$ А также поскольку $SO$ — высота, то $BC ⊥ OS.$ Тогда $BC$ перпендикулярна $SOH,$ в частности, перпендикулярна и к $OP.$ Тогда получается, что $OP$ перпендикулярна к $SH,BC,$ а значит, $OP = 2√2$ как расстояние от основания высоты до боковой грани.

Положим, что $OH = x,$ тогда $AO = x√2$ так как в квадрате диагональ в $√2$ раз длиннее стороны. Теперь запишем отношения площадей прямоугольных треугольников $ASO$ и $SOH :$

- -SASO- -AO √ - AS-⋅OQ- AS-⋅2√-3 SSOH = OH = 2= SH ⋅OP = SH ⋅2√ 2

AS 2 SH-= √3-

Теперь пусть $AS =2a,$ тогда $√- SH =a 3.$ А из прямоугольного треугольника $SHC$ по теореме Пифагора $HC = a= OH = x.$ Теперь же из треугольника $SOH$ по теореме Пифагора:

OS = x√2

Тогда по формуле высоты для этого же треугольника:

√ - 2√2 = x-√2⋅x x 3

√ - x = 2 3

Наконец, по формуле объема пирамиды:

VSABCD = 1x⋅4x2 = 32√6. 3

Ответ:

$32√6$

Ошибка.
Попробуйте повторить позже

Задача 5#69375

Боковые рёбра треугольной пирамиды попарно перпендикулярны, а стороны основания равны $√61-$ , $√52-$ , $√41$ . Центр сферы, которая касается всех боковых граней, лежит на основании пирамиды. Найдите радиус этой сферы.

Источники: Звезда - 2023 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Для начала, можно найти оставшиеся длины ребер: у нас же они перпендикулярны, а значит, можно применить теорему Пифагора!

Подсказка 2

С длинами разобрались, а что делать с радиусом вписанной сферы? На плоскости у нас есть полезный факт, что r = S/p, где S - площадь треугольника, а p - полупериметр. Если вы помните доказательство этого факта, то проведите аналогичные рассуждения здесь)

Подсказка 3

Если не помните, то сделайте вот что: вот у нас есть центр сферы O. Проведем отрезки из O ко всем вершинам пирамиды. Тогда он разбивается на 3 маленьких тетраэдра. Тогда его объем - сумма объемов маленьких тетраэдров. А чему равны объемы маленьких тетраэдров?)

Подсказка 4

А они равны 1/3 × r × (площадь грани). Причем площадь грани очень легко посчитать т.к. боковые ребра - перпендикулярны, и их длины мы знаем! Осталось ещё вспомнить формулу объема пирамиды у которой боковые ребра перпендикулярны, и дело в шляпе!

Показать ответ и решение

$PIC$

Обозначим основание пирамиды — $ABC$ , вершину пирамиды — $D$ , центр сферы — $O$ , радиус сферы — $r$ . Пусть $√-- √ -- √-- AB = 41,BC = 61,AC = 52$ . Обозначим $AD = x,BD = y,CD = z$ .

Так как радиус, проведённый в точку касания сферы и плоскости, ортогонален плоскости, имеем:

VABCD =VABDO + VBCDO +VACDO =

= 13SABD ⋅r+ 13SBCD ⋅r+ 13SACD⋅r=

( ) = 1r 1xy+ 1yz+ 1zx 3 2 2 2

С другой стороны, так как боковые рёбра попарно перпендикулярны, то

1 VABCD = 6xyz

Поэтому

xyz r= xy-+yz+-xz

Числа $x,y,z$ находятся из системы уравнений:

( |||{ x2+y2 = 41 x2+z2 = 52 |||( y2+z2 = 61

Складывая уравнения системы и деля на два, получим:

2 2 2 x + y +z = 77

откуда $x2 = 16,y2 = 25,z2 =36$ . Тогда

r= ---4-⋅5-⋅6-----= 60- 4⋅5+4 ⋅6 +5⋅6 37

Ответ:

$60 37$

Ошибка.
Попробуйте повторить позже

Задача 6#90509

Найдите объём правильной четырёхугольной пирамиды со стороной основания равной 1, если известно, что плоские углы при вершине равны углам наклона боковых рёбер к плоскости основания.

Источники: ДВИ - 2023, вариант 233, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть пирамида — SABCD и её высота — SН. Плоский угол при вершине назовём α. SA = x. Отметьте равные углы и давайте двумя способами найдём cos(α): по теореме косинусов из △SAD и как отношение АН/SA

Подсказка 2

Решение квадратного уравнения поможет нам вычислить х. Какой из корней получился посторонним?

Подсказка 3

ОТТ поможет нам найти sin(α) и затем, с его помощью, высоту. Осталось лишь внимательно поработать с некрасивыми числами и записать ответ!

Показать ответ и решение

Пусть $SABCD$ — данная правильная четырехугольная пирамида с вершиной $S$ и высотой $SH, AB = 1.$ Обозначим $∠BSC = ∠SCH = ∠α.$

$PIC$

Из прямоугольного треугольника $CSH$ находим, что

1√- SC = --CH----= --2-= √-1--- cos∠SCH cosα 2cosα

Пусть $M$ — середина ребра $BC.$ Из прямоугольного треугольника $CSM$ находим, что

--CM---- --12--- --1---- SC = sin∠CSM = sin(α2) = 2sin(α2)

Значит,

( ) √-1---= --1-α =⇒ √2sin α-= cosα 2cosα 2sin 2 2

2(α) 2 2 sin 2 = cosα

2 2 1− cosα =cos α =⇒ cos α+ cosα− 1= 0 =⇒

√5−-1 cosα = 2

Тогда

∘-------- ∘ ---√----- ∘ ---√-- tg α= -1---− 1= 3+--5− 1= 1+--5 cos2α 2 2

√- ∘---√-- ∘ ----- SH = CH ⋅tgα= -2-⋅ 1-+--5= 1 1+√ 5 2 2 2

Следовательно,

∘ ----- ∘ --√-- VSABCD = 1SABCD ⋅SH = 1⋅1⋅ 1 1+√5-= --1+--5 3 3 2 6

Ответ:

$√1+-√5 6$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#37326

В тетраэдре $ABCD$ плоские углы при вершине $D$ прямые. Пусть $h$ — длина высоты $DO$ тетраэдра, $a,b,c$ — длины ребер, выходящих из вершины $D$ . Докажите, что

1 1 1 1 h2 = a2 + b2-+ c2.

Подсказки к задаче

Подсказка 1

Надо доказать о том, что квадрат чего-то равен сумме квадратов. Давайте для начала подумаем об аналогии с планиметрией. Нет ли там чего-то похожего и есть ли такое в стереометрии?

Подсказка 2

Верно, в планиметрии есть теорема Пифагора для прямоугольного треугольника. Но ведь и здесь у нас прямые углы, причём целых три штуки. Точно! На вебинаре МО рассказывал о таком. Осталось только выразить площади.

Подсказка 3

Ага, видим, что площадь треугольника АВС выразить сразу не получится. Но ведь нам нужно ещё воспользоваться высотой h. Может, тогда удастся вспомнить формулу, в которой она используется?

Показать ответ и решение

$PIC$

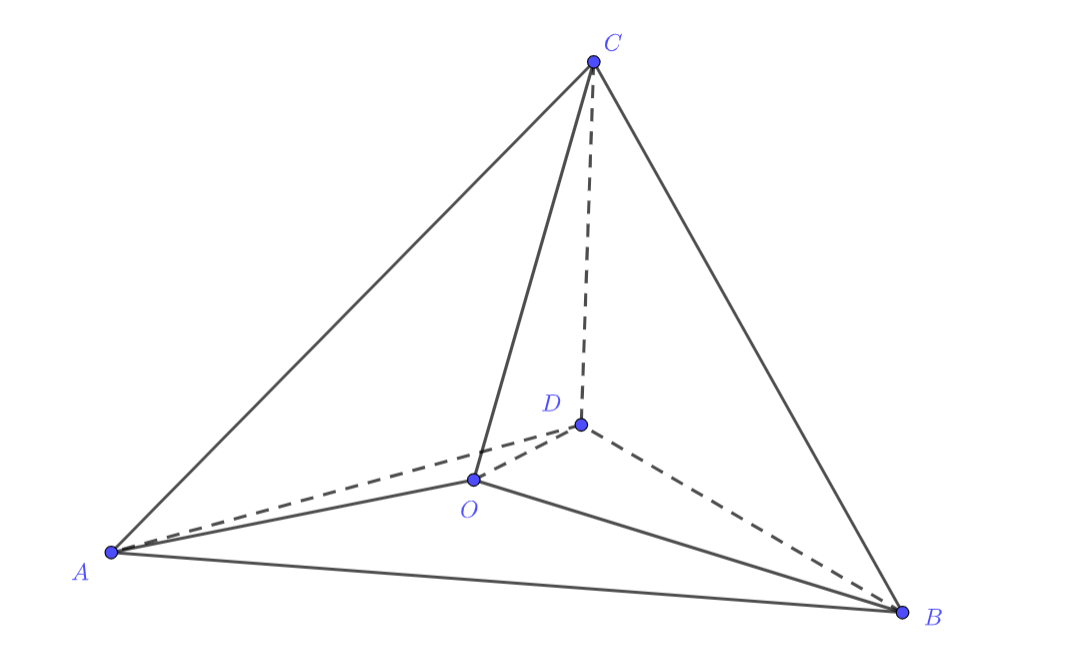
Так как все плоские углы при вершине $D$ прямые, то:

во-первых, запишем объём двумя способами:

1)VABCD = 1p(A,BCD )⋅SBCD = 1abc 3 6

2)VABCD = 1h ⋅SABC 3

откуда

abc= 2h⋅SABC;

во-вторых, по пространственной теореме Пифагора для прямоугольного тетраэдра

2 2 2 2 SABC = SACD +SABD + SBCD

Выражаем площади:

(abc)2 = (ab)2+ (bc)2+ (ac)2 2h 2 2 2

Отсюда немедленно получаем:

1- 1- 1- 1- h2 = a2 + b2 + c2

Ответ:

что и требовалось доказать

Ошибка.
Попробуйте повторить позже

Задача 8#38772

Плоские углы трехгранного угла равны $α,β,φ$ , противолежащие им ребра трехгранного угла образуют с плоскостями граней углы $a$ , $b$ , $c$ . Докажите, что

sin αsina= sinβ sinb= sinφsin c.

Подсказки к задаче

Подсказка 1

Для начала давайте попробуем сделать задачу более "осязаемой". У нас есть просто множество углов и непонятно, что с ними в таком виде делать. О какой фигуре, возможно, вы подумали при виде такой конструкции? Нельзя ли в этой задаче до неё просто достроить?

Подсказка 2

Верно, мы ведь можем просто представить тетраэдр с нужным нам трехгранным углом и уже работать с ним. Давайте ещё ведём длины рёбер x, y, z тетраэдра смежных с трёхгранным углом. Выходит, нам надо доказать тройное равенство... Но просто его выводить, скорее всего, не получится. Тогда раз три произведения равны между собой, возможно, они равны чему-то общему, что от нас "спрятали". Попробуем решить задачу так. Раз мы уже зафиксировали рёбра, и углы нам даны, что не будет меняться в нашем тетраэдре?

Подсказка 3

Точно, объём у нас уже не будет меняться, а стороны мы зафиксировали сами, поэтому можно попробовать связать синусы с ними. Для нахождения объёма нужна высота и площадь основания. Не можем ли мы их просто найти из имеющихся данных?

Подсказка 4

Конечно, площадь основания находится почти "бесплатно", а высота – из конструкции с прямоугольным треугольником, у которого известна гипотенуза и угол. Осталось только выразить нужные произведения оттуда и приравнять между собой.

Показать ответ и решение

Рассмотрим произвольный тетраэдр, содержащий заданный трёхгранный угол. Пусть $x,y,z$ ( $x$ соответствует углу $a$ и т.д.) — длины смежных с трёхгранным углом сторон этого тетраэдра. Заметим, что

xyzsinα sina= h⋅yzsinα =hyz ⋅2Syz = 6V

Где $hyz$ — длина высоты на грань со сторонами $y,z$ , а $Syz$ — её площадь, $V$ — объём тетраэдра. Отсюда следует, что каждое произведение равно $6V- xyz$ .

Ответ:

что и требовалось доказать

Ошибка.
Попробуйте повторить позже

Задача 9#71442

В треугольной пирамиде $SABC$ в основании лежит равнобедренный прямоугольный треугольник $ABC$ с гипотенузой $AC.$ Боковые грани $SAB$ и $SAC$ перпендикулярны плоскости $ABC.$ Сфера радиусом, равным $AC,$ с центром в точке $S$ делит пирамиду на две части. Найдите объём большей из этих частей, если $SA= AB = 2.$

Источники: ПВГ-2022, 11.5 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Из условия сразу можно понять, что SA перпендикулярно плоскости ABC. Работать просто так с пирамидой не очень удобно, к тому же у нас ещё присутствует сфера в задаче. Видим, что у нас прямой угол в основании и прямой угол между ребром и основанием! Тогда до чего можно достроить нашу пирамиду?

Подсказка 2

Верно, можно сначала отразить симметрично пирамиду относительно AC. А дальше понятно, что это большая пирамида будет 1/3 от куба, до которого тоже в силу равенства отрезков можно достроить. Но хватит ли этого нам? У нас есть сфера, которая отсекает от исходной пирамиды часть, и не совсем понятно, как вообще этот объём искать... Как можно задействовать неиспользуемую часть, после чего всё станет намного проще?

Подсказка 3

Да, можно наш куб со стороной равной двум достроить ещё до куба со стороной 4. Теперь какой же объём нас интересует?

Подсказка 4

Верно, нам нужен объём, который получается, как разность объёма сферы и 6 сегментов, выходящих наружу за куб. А точнее, потом нам нужно поделить его на 48. Отлично! Осталось аккуратно посчитать эти объёмы, и потом ещё проверить, что вы нашли больший из них. Например, можно проверить, что найденный объём больше половины объёма исходной пирамиды. Победа!

Показать ответ и решение

$PIC$ $PIC$

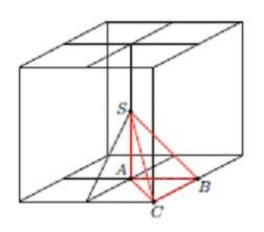
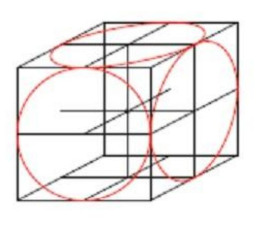
Из условия задачи вытекает, что ребро $SA$ пирамиды перпендикулярно основанию $ABC.$

Обозначим $SA = AB =a.$ Пирамида $SABCD$ является $1∕48$ частью изображённого на рисунке куба с ребром $2a,$ причём все 48 пирамид, образующих этот куб, располагаются центрально-симметрично относительно общей вершины $S.$

Поэтому искомый объём есть $1∕48$ объёма тела, представляющего собой пересечение шара радиуса $√ - R = 2a$ и данного куба. Это пересечение есть шар без шести шаровых сегментов с высотой шарового сегмента $- h= (√2− 1)a$ (см. рисунок).

Объём этого тела:

( √- ) V = 4πR3 − 6πh2(R − h) = 4π⋅2√2a3− 6π(√2− 1)2 √2−-2-− 1 a3 = 3 3 3 3

√ - = 8-2πa3− 2(3− 2√2-)(2√2+ 1)πa3 = 2 ⋅πa3(4√2− 3(4√2 − 5))= 2⋅πa3(15− 8√2-) 3 3 3

Значит, искомый объём равен

√- √- -2--⋅πa3(15− 8√2) = πa3(15− 8-2) = π(15−-8-2) 3⋅48 72 9

Отметим, что объём всей пирамиды равен $1 2⋅2 4 3 ⋅ 2 ⋅2 =3$ (или, что то же самое, $1∕48$ части куба, то есть $43 4 48 = 3$ ) Найденный объём части пирамиды больше, чем $1∕2$ объема пирамиды, так как

√- π(15−-8-2)> 2⇔ 15− 8√2> -6⇔ 15− 8√2> 15− 12 =3 >-6 9 3 π π

Это подтверждает, что мы нашли именно объём большей части пирамиды.

Ответ:

$π(15−-8√2) 9$

Ошибка.
Попробуйте повторить позже

Задача 10#72972

Звездолёт находится в полупространстве на расстоянии $a$ от его границы. Экипаж знает об этом, но не представляет, в каком направлении двигаться, чтобы достигнуть граничной плоскости. Звездолёт может лететь в пространстве по любой траектории, измеряя длину пройденного пути, и имеет датчик, подающий сигнал, когда граница достигнута. Может ли звездолёт гарантированно достигнуть границы, преодолев путь длиной не более $14a?$

Источники: ММО-2022, 11.4 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

В условии сказано, что пройдя расстояние, равное a, в определенную сторону, звездолет покинет полупространство. Каким образом мы можем описать все варианты той точки, где кончается полупространство?

Подсказка 2

Мы можем сказать, что если звездолет находится в какой-нибудь точке О, то на сфере с центром в точке O и радиусом a гарантированно найдется точка , которая уже не будет являться частью полупространства. Подумайте, как данная сфера может помочь в выборе траектории. Может быть, есть какая-то фигура, которую удобно будет описать около сферы?

Подсказка 3

Рассмотрите правильный октаэдр, описанный около данной сферы. Если мы докажем, что путь из центра октаэдра по всем вершинам без повторений меньше 14a и хотя бы одна вершина гарантировано не лежит в полупространстве, то мы решим задачу. Сначала подумайте, как можно сделать второе.

Подсказка 4

Воспользуемся методом от противного. Подумайте, где возникает противоречие, если мы скажем, что все вершины октаэдра лежат в данном полупространстве.

Подсказка 5

Теперь нужно найти длину пути от О и по всем вершинам. Давайте назовем наш октаэдр A₁A₂A₃A₄A₅A₆, тогда не трудно найти кратчайший маршрут обхода: O -> A₁ -> A₂ -> A₃ -> A₄ -> A₅ -> A₆. Как можно найти длину данного пути?

Подсказка 6

Для начала нужно найти длину отрезка OA₁, так как из него легко можно выразить длину ребра октаэдра. Мы знаем, что длина высоты, опущенной из точки О на грань октаэдра равна a, Тогда как мы можем найти длину OA₁?

Подсказка 7

Давайте рассмотрим пирамиду OA₁A₂A₃, найдем ее объем двумя разными способами, как 1/6 куба с ребром OA₁ и через длину высоты и площадь A₁A₂A₃. Из равенства двух данных выражений легко можно выразить OA₁. Для окончательного решения останется только найти длину ребра и доказать, что предложенный нами маршрут меньше 14a.

Показать ответ и решение

$PIC$

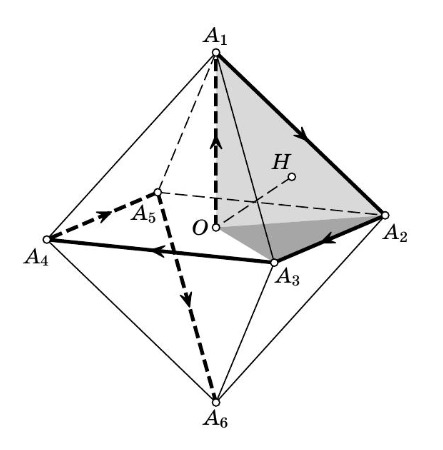
Пусть корабль находится в некоторой точке $O.$ Рассмотрим правильный октаэдр $A1A2A3A4A5A6,$ описанный возле шара радиуса $a$ с центром в точке $O.$ Докажем, что путь $O → A1 → A2 → A3 → A4 → A5 → A6$ заведомо позволит достигнуть граничной плоскости.

Предположим противное. Тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен $a,$ тоже лежит строго внутри полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно $a.$

Покажем теперь, что длина пути $O→ A1 → A2 → A3 → A4 →$ $→ A5 → A6$ меньше $14a.$ Пусть $OA1 =OA2 = OA3 = x,OH$ — высота пирамиды $OA1A2A3.$ Запишем ее объём двумя способами:

√- V = 1x3 = 1⋅OH ⋅S = 1⋅a⋅√3 ⋅ (x-2)2 6 3 A1A2A3 3 4

Отсюда получаем, что $√- x= a 3,$ а длина ребра октаэдра равна $√- a 6.$ Поэтому длина пути равна $√ - √- ( 3+5 6)a< 14a,$ так как $√ - 2< 43∕30.$

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 11#90137

Объём треугольной призмы $ABCA ′B′C′$ с основанием $ABC$ и боковыми рёбрами $AA′,BB ′$ , $CC ′$ равен 72. Найдите объём тетраэдра $DEF G$ , где $D$ — центр грани $′ ′ ABB A,E$ — точка пересечения медиан треугольника $′ ′ ′ A BC ,F$ — середина ребра $AC$ и $G$ — середина ребра $BC.$

Источники: ДВИ - 2022, вариант 221, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Лежащих в одной или хотя бы в параллельных плоскостях, оснований у призмы и тетраэдра не видно. Значит попробуем достроить удобную для вычисления фигуру, с помощью которой можно найти искомый объём через отношение.

Подсказка 2

Продлим ED до пересечения с плоскостью АВС, назовём I полученную точку. Как связаны объёмы тетраэдров IEFG и DEFG?

Подсказка 3

Связать объём тетраэдра IEFG с объёмом призмы можно взяв за основание тетраэдра △IFG: как его сторона FG и высота к этой стороне связаны с высотой и сторонами △АВС? Осталось аккуратно записать все найденные отношения и мы получим ответ!

Показать ответ и решение

Пусть $C′H$ и $CJ$ — медианы верхней и нижней грани, тогда $D$ лежит на $HJ$ — в центре средней линии параллелограмма. Отсюда следует, что при отражении $E$ относительно $D$ мы попадём на $CJ$ — в точку $I$ , то есть $VDEFG =VEFGI∕2$ .

$PIC$

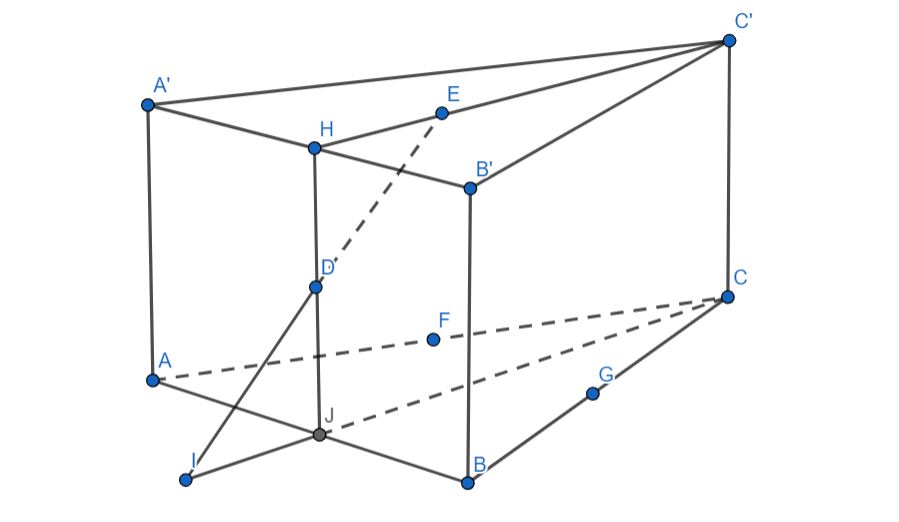
Также в силу симметрии $JI = HE = EC∕2$ ( $E$ — точка пересечения медиан), тогда $CI = 2⋅EC = 4∕3 ⋅CJ$ , однако заметим, что $FG$ делит $CJ$ пополам, то есть делит $CI$ в отношении $3 :5$ от вершины $C$ , откуда

SIFG = 5∕3⋅SCFG = 5∕12 ⋅SABC,

при этом высота совпадает с высотой призмы, откуда

VDEFG = VEFGI∕2= 5∕24⋅1∕3⋅SABC ⋅h =5,

где $h$ — та самая высота.

Ответ: 5

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#76664

Боковое ребро правильной треугольной пирамиды наклонено к плоскости ее основания под углом $45∘$ . В пирамиду вписан куб так, что четыре его вершины лежат на основании пирамиды, а другие четыре — на ее боковых гранях. Найти отношение объемов куба и пирамиды.

Источники: Росатом - 2021, 11.6, комплект 3 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала обозначим за a ребро пирамиды. Получается нам нужно выразить объёмы фигур через a. Начнём с пирамиды. Для объёма нам нужны основание и высота. Так как пирамида у нас правильная, то куда падает её высота?

Подсказка 2

Верно, в центр основания правильного треугольника, то есть в центр описанной окружности. Теперь радиус мы можем легко найти, а угол будет как раз тот самый из условия. Отлично, высота найдена. А площадь основания равна площади правильного треугольника. Давайте теперь попробуем разобраться с кубом. Удобно будет ввести ребро куба b и попробовать выразить его через a. Тогда будет победа. Но какую ещё вспомогательную фигуру хочется рассмотреть, учитывая расположение куба?

Подсказка 3

Да, давайте рассмотрим сечение, которое получается из-за куба. Понятно, что это будет треугольник, подобный основанию, и мы даже знаем коэффициент подобия треугольников. То есть мы знаем длину стороны сечения. Как теперь можно вторым способом посчитать это основание?

Подсказка 4

Верно, рассмотрим сечение как треугольник, внутрь которого вписан квадрат. Мы легко можем выразить, как сумму отрезков, сторону треугольника через b. Наконец с помощью равенства из прошлой подсказки выражаем b через a и находим объём куба. Осталось только посчитать отношение, и победа!

Показать ответ и решение

Пусть $a$ – сторона основания, $α= 45∘$ – угол наклона бокового ребра, $H$ – высота пирамиды, $R = AO$ — радиус окружности, описанной около основания. В правильном треугольнике со стороной $a$ радиус описанной окружности: $a√- R= AO = 3$ .

Из прямоугольного треугольника $SAO$ находим высоту пирамиды: $a√- H = AO ⋅tgα = 3$ .

$PIC$

Площадь основания пирамиды

√ - S = 1a⋅a⋅sin(60∘)= a2-3 2 4

Объем пирамиды:

1 1 a2√3 a a3 V1 = 3S⋅H = 3 ⋅-4 ⋅√3-=12

Пусть $b$ ребро вписанного куба и $A1B1C1$ – сечение пирамиды плоскостью верхней грани куба.

$PIC$

Обозначим через $a1$ сторону треугольника этого сечения $a1 =A1B1$ . Треугольники $ABC$ и $A1B1C1$ подобны с коэффициентом подобия: $k = H−b= a−b√3 H a$ .

И поэтому $a = ka= a− b√3 1$ .

Рассмотрим треугольник $A B C 1 1 1$ со вписанной гранью куба.

$PIC$

Сторона

b b 2+√3- a1 =A1K + KN + NB1 = tg60∘ + b+ tg-60∘-=-√3--b

Приравнивая два выражения для $a1$ , находим $b$ : $√ - b = 5+√33a$ .

Так как объем куба $V2 = b3$ , то искомое отношение объемов:

√- V2 (5+3√3a)3 --36√3--- V1 = a3 = (5+√3-)3 12

Ответ:

$--36√3-- (5+ √3)3$

Ошибка.
Попробуйте повторить позже

Задача 13#95856

В правильной четырёхугольной пирамиде $ABCDS$ площадь основания совпадает с площадью боковой грани и равна $1.$ $M$ — точка пересечения медиан грани $CDS$ . Точка $N$ лежит на прямой $AM$ и $AN :NM = 3:4.$ Найдите сумму расстояний от точки $N$ до всех граней пирамиды.

Источники: Звезда - 2021, 11.2 (см. zv.susu.ru)

Показать ответ и решение

$PIC$

Из условия задачи сторона основания пирамиды равна $1$ , апофема боковой грани — $2.$ Тогда высота пирамиды $∘---- √-- h= 4 − 14 =-125 .$ Объём пирамиды $ABCDS$ равен $√-- V = -165.$

С другой стороны, объём пирамиды можно найти как сумму объёмов пяти пирамид, вершина которых — точка $N$ , а основания — грани пирамиды $ABCDS$ . Тогда $V = 13 ⋅(h1+ h2+h3+ h4+ h5)⋅1$ , где $h1,h2,h3,h4,h5$ — расстояния от точки $N$ до граней пирамиды $ABCDS$ (или высоты маленьких пирамид). Приравнивая объёмы, получаем

√15- h1+ h2+ h3+ h4 +h5 = 2

Заметим при этом, что сумма расстояний не зависит от расположения точки внутри данной пирамиды.

Ответ:

$√15 2$

Ошибка.
Попробуйте повторить позже

Задача 14#38690

Единичный куб $ABCDA B C D 1 1 1 1$ повёрнут на $90∘$ вокруг прямой, проходящей через середины противоположных рёбер $AD$ и $B C 1 1$ . Найдите объём общей части исходного куба и повёрнутого.

Источники: ОММО-2013, номер 10, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Итак, для начала надо внимательно разобраться с получающейся фигурой. Удобно начать построение с поворота рёбер AD и B₁C₁. Похожа ли общая часть кубов на какую-то известную нам фигуру? Если нет, то подумайте как можно её разбить на составляющие.

Подсказка 2

Работать с такого типа фигурой можно через сумму объёмов составляющих её частей. Или же через разность: вычитая удобные части из фигуры, содержащей искомую. Рассмотрим способ через сумму — наш многогранник удачно разбивается на параллелепипед и две правильные четырёхугольные пирамиды.

Подсказка 3

Найти все нужные длины нам поможет Пифагор: рассмотрите одну из граней исходного куба и возвышающуюся над ней часть нового куба. Аккуратный счёт поможет вам узнать, где пересекутся рёбра нового и исходного кубов.

Подсказка 4

Также, с помощью Пифагора мы сможем отыскать и все рёбра искомого многогранника. Осталось лишь отыскать объёмы всех составных частей и сложить их. Задача убита!

Показать ответ и решение

$PIC$

Пусть $S$ и $S1$ — середины $AD$ и $B1C1$ , а куб после поворота переходит в $A′B′C ′D′A′1B′1C′1D′1$ . Общая часть будет объединением прямоугольного параллелепипеда $EFGHE1F1G1H1$ и двух симметричных правильных четырёхугольных пирамид $SEFGH$ и $S1E1F1G1H1$ , найдём их объёмы.

$PIC$

Сторона основания пирамиды равна стороне квадрата, то есть единице. Далее оба квадрата симметричны относительно $AB1C1D$ , потому $E1√F1 √1- E1B1 = F1B1 = 2 = 2$ . Из $△E1B1S1$ имеем $∘-1--1 √3 E1S1 = 2 + 4 = 2$ — боковая сторона пирамиды. Отсюда легко найти её высоту, которая равна $1 2$ , тогда объём пирамиды равен $1 1 1 3 ⋅1 ⋅2 = 6$ .

$PIC$

Поскольку $A1E1 = A1E = 1− 1√2$ ( $EE1 ⊥E1F1$ , которая по доказанному образует углы $45∘$ со сторонами), то $EE1 = √2 − 1$ , $EF = EH = 1$ , как стороны квадрата, отсюда объём параллелепипеда $√2 − 1$ .

В итоге объём сечения $16 ⋅2+ √2 − 1= √2-− 23$ .

Ответ:

$√2-− 2 3$

Ошибка.
Попробуйте повторить позже

Задача 15#70627

В основании прямой призмы $ABCA ′B′C ′$ лежит прямоугольный треугольник $ABC$ , такой что $AC = BC = 1$ . На ребре $A′B′$ верхнего основания (параллельном $AB$ ) отмечена точка $D$ , так что $′ ′ AD :DB =1 :2$ . Найдите радиус сферы, вписанной в тетраэдр $′ ABC D$ , если высота призмы равна $1.$

Источники: ДВИ - 2013, вариант 2, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Нам надо как-то найти радиус вписанной сферы. Его можно найти в формуле для объема тетраэдра. Можно ли как-то просто найти этот объем?

Подсказка 2

На самом деле он равен объему тетраэдра ABCD, ведь CC' параллельна основанию ABD. А объем тетраэдра легко найти: мы знаем, что площадь основания ABC- это 1/2, а высота- 1 ⇒объем равен 1/6. Что нам еще надо найти?

Подсказка 3

Как мы знаем, V=r*S/3, где V- объем тетраэдра, r- радиус сферы и S- площадь полной боковой поверхности. Тогда r=1/(2S). Легко заметить, что все стороны тетраэдра ABC'D легко находятся с помощью теоремы Пифагора. Тогда, зная все стороны, можно будет найти площади боковых граней и завершить решение. Я в вас верю!

Показать ответ и решение

$PIC$

Из теоремы Пифагора в треугольнике $ABC$ сторона $√- AB = 2.$ Так как $A ′D :DB′ = 1:2$ и $√- A′B′ = 2,$ то $√- √- A′D = 32,DB ′ = 232.$

Обозначим объём тетраэдра $ABC ′D$ , площадь его поверхности и радиус вписанной в него сферы, соответственно, как $V,S,r$ . Тогда $V = 13rS$ . Объём тетраэдра $ABC′D$ paвен объёму тетраэдра $ABCD$ , поскольку $CC′∥AA′$ . Стало быть,

V = 1∕6 =⇒ r= (2S)−1

Найдём все рёбра пирамиды $DABC ′.$ По теореме Пифагора в $△AA ′D:$

( √-)2 √ -- AD2 = A′A2+ A′D2 = 12+ -2- = 11 =⇒ AD = --11 3 9 3

Аналогично из теорем Пифагора в треугольниках $BB ′D,ACC′$ и $BCC ′ :$

┌│----(----)- -- │∘ 2 2√-2 2 √17 ′ ∘-2---2 √- ′ ∘ -2--2- √- BD = 1 + 3 = 3 ; AC = 1 + 1 = 2; BC = 1 +1 = 2

Так как $A′C′ = B′C′,$ то $∠C′A ′D = 45∘,$ тогда по теореме косинусов в $△DA ′C′ :$

′ 2 2 √2 1 5 ′ √5- C D = 9 + 1− 2⋅ 3-⋅√2-= 9 =⇒ C D= -3-

Теперь найдём площади всех граней пирамиды $DABC ′.$

$√- SADB =-22 .$ Так как $△AC ′B$ — равносторонний, то $√- SAC′B = -32 .$

Рассмотрим $△AC ′D.$ Пусть $∠AC′D =α,$ тогда по теореме косинусов

√ - ∘ -- 11= 2+ 5− 2⋅√2⋅--5⋅cosα =⇒ cosα= √2- =⇒ sinα = 3 9 9 3 10 5

1 √- √5 1 SAC′D = 2 ⋅ 2⋅-3-⋅sinα =√6

Рассмотрим $△BC ′D.$ Пусть $∠BC ′D = β,$ тогда по теореме косинусов

√ - 17-= 2+ 5− 2⋅√2⋅--5⋅cosβ =⇒ cosβ = √1- =⇒ sinβ = √3- 9 9 3 10 10

1 √ - √5 1 SBC′D = 2 ⋅ 2⋅-3-⋅sinβ = 2

Тогда площадь поверхности тетраэдра $′ ABC D$

( - - ∘-) S =SADB + SAC′B + SAC′D + SBC′D = 1 1+√ 2+√ 3+ 2 2 3

Остаётся воспользоваться соотношением $r =(2S)−1.$

Ответ:

$(1+ √2+ √3+ ∘ 2)−1 3$

Ошибка.
Попробуйте повторить позже

Задача 16#99414

Дана сфера радиуса $1$ с центром в точке $O.$ Из точки $A,$ лежащей вне сферы, проведены четыре луча. Первый луч пересекает поверхность сферы последовательно в точках $B1$ и $C1,$ второй — в точках $B2$ и $C2,$ третий — в точках $B3$ и $C3,$ четвертый — в точках $B4$ и $C4.$ Прямые $B1B2$ и $C1C2$ пересекаются в точке $E,$ прямые $B3B4$ и $C3C4$ — в точке $F.$ Найдите объем пирамиды $OAEF,$ если $AO = 2,EO = FO =3,$ а угол между гранями $AOE$ и $AOF$ равен $∘ 30 .$

Показать ответ и решение

Рассмотрим сечение сферы плоскостью $B B C C . 1 2 1 2$ Пусть $M$ — вторая точка пересечения окружностей, описанных около треугольников $AB1B2$ и $EC2B2.$ Из цепочки равенств

∘ ∠AMB2 = 180 − ∠AB1B2 =

= ∠C B B = 180∘− ∠C C B =∠EC B = 180∘− ∠EMB 1 1 2 1 2 2 2 2 2

следует, что точка $M$ лежит на отрезке $AE.$ По теореме о равенстве произведений отрезков секущих,

AM ⋅AE = AB2⋅AC2 =(AO − r)(AO + r)=AO2 − r2 =3

(здесь $r=1$ — радиус сферы). Точно так же $EM ⋅EA= EO2 − r2 =8.$ Отсюда $AE2 = AE(AM + EM )= 11.$ Аналогично получаем $AF 2 = 11.$ Значит, грани $AOE$ и $AOF$ равны по трем сторонам и имеют площадь $√-- S =-325$ по формуле Герона(нам известны все три стороны).

$PIC$

Давайте теперь найдём высоту грани $AOE.$ Опустим перпендикуляр $EH.$ Посчитаем длину через подсчёт площади двумя способами:

√35- EH -2- = -2-⋅2

Откуда $√35 EH = -2 .$ Рассмотрим теперь плоскость $EHF$ и опустим в ней высоту $ER.$ Тогда по теореме о трёх перпендикулярах $F H$ будет перпендикулярно $AO.$ Тогда из условия понимаем, что $∠EHF = 30∘,$ так как это и будет угол между плоскостями. К тому же $AO$ перпендикулярно всей плоскости $EF H,$ так как он перпендикулярен двум прямым из этой плоскости. Но тогда $ER$ перпендикулярно $FH$ и $AO,$ откуда $ER$ — это перпендикуляр к плоскости. Тогда найдём $ER$ и решим задачу. Из прямоугольного треугольника $HER$ с углом $30∘$ понимаем, что $√-- ER = -345.$ Отсюда объём пирамиды будет:

√-- √ -- VAEFO = 1⋅ER ⋅SAOF = 1 ⋅-35⋅-35= 35 3 3 2 4 24

$PIC$

Ответ:

$35 24$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#70626

Основанием пирамиды $SABCD$ является трапеция $ABCD$ с основаниями $BC$ и $AD$ такими, что $BC :AD = 2:5$ . Диагонали трапеции пересекаются в точке $E$ , а центр $O$ вписанной в пирамиду сферы лежит на отрезке $SE$ и делит его в отношении $SO :OE =7 :2$ . Найти площадь полной поверхности пирамиды, если площадь боковой грани $SBC$ равна $8.$

Источники: Вступительные на МехМат МГУ, 1999, задача 6

Подсказки к задаче

Подсказка 1

У нас уже есть площадь одной боковой грани. Может, тогда попытаемся найти площади остальных? Подумайте, как соотносятся между собой площади треугольников △SBC и △SAB...

Подсказка 2

Вроде как, напрямую связь между ними установить не получается. Давайте попробуем посмотреть на объемы тетраэдров SAOB и SBOC: они относятся как площади треугольников △SAB и △SBC. А как еще можно найти их отношение?

Подсказка 3

Т.к. объемы SABE и SBCE относятся как площади △ABE и △BEC (то есть как AE к EC), а также объемы OAEB и OBEC относятся как эти площади, то и их разности (то есть SAOB и SBOC) относятся как AE к EC. Тогда верно равенство S(△SAB)/S(△SBC)=AE/EC ⇒ S(△SAB)=20. Теперь найдите площади остальных боковых граней!

Подсказка 4

Нам осталось только найти площадь основания (назовем ее S₀). Мы знаем, что O делит SE в отношении 7/2. Тогда r=h*2/9, где r- радиус вписанной сферы, а h- высота пирамиды. Мы знаем, что V=S₀*h*1/3=S₀*r*3/2, где V- объем нашей пирамиды. Как еще, зная площади боковых граней, можно выразить V?

Подсказка 5

Через объемы тетраэдров ESAB, ESBC, ESCD и ESDA! Про них мы знаем, что высоты, опущенные из вершины E, равны r*9/7. Тогда мы без проблем сможем записать V через сумму объемов этих тетраэдров, приравнять к S₀*r*3/2 и найти площадь основания!

Показать ответ и решение

$PIC$