Сечение шара плоскостью
Ошибка.
Попробуйте повторить позже
Из центра сферы радиуса
проведены три луча, пересекающие сферу в точках
и
Известно, что
Найдите площадь части сферы, ограниченной плоскостями
и
Источники:
Подсказка 1
Рассмотрите сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен φ. Плоскости пересекают сферу по большим окружностям. На их пересечении получается криволинейный треугольник. Выразите его площадь через радиус и угол!
Подсказка 2
Три плоскости (содержащие грани трехгранного угла) разбивают сферу на 8 криволинейных треугольников. Искомую площадь криволинейного треугольника ABC обозначим через S, а его углы (которые, очевидно, являются двугранными углами трехгранного угла OABC ) за φ, ψ, θ. Примените формулу для площади криволинейного треугольника с углами φ, ψ, θ.
Подсказка 3
Примените теорему косинусов для трехгранного угла!
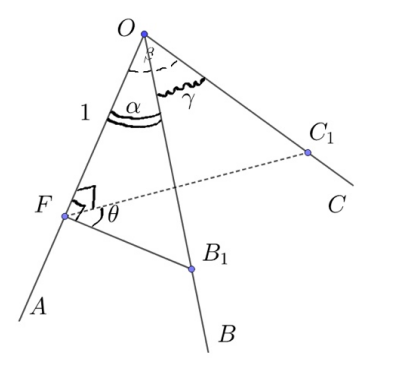
В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого
треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать
Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен
Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол
Площадь поверхности сферы равна
Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно
пропорциональна величине
и равна
![]()
Три плоскости (содержащие грани трехгранного угла) разбивают сферу на треугольников. Искомую площадь криволинейного
треугольника
обозначим через
а его углы (которые, очевидно, являются двугранными углами трехгранного угла
за
Площади криволинейных треугольников, примыкающих к сторонам треугольника
обозначим
С каждым из этих
треугольников
образует «дольку», поэтому
Оставшиеся из
-х нерассмотренных
криволинейных треугольников симметричны
-м рассмотренным относительно центра сферы. Значит, суммарная площадь
рассматриваемых четырех треугольников равна половине площади сферы, то есть
Тогда сложим первые три
уравнения и воспользуемся четвертым:
![]()
Из теоремы косинусов для трехгранного угла
Отсюда получаем ответ.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




