Тема Сферы

Сечение шара плоскостью

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела сферы

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68100

Из центра $O$ сферы радиуса $R$ проведены три луча, пересекающие сферу в точках $A,B$ и $C.$ Известно, что $∠AOB =∠AOC =∠BOC =60∘.$ Найдите площадь части сферы, ограниченной плоскостями $(AOB ),(AOC)$ и $(BOC).$

Источники: Межвед-2023, 11.8 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Рассмотрите сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен φ. Плоскости пересекают сферу по большим окружностям. На их пересечении получается криволинейный треугольник. Выразите его площадь через радиус и угол!

Подсказка 2

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на 8 криволинейных треугольников. Искомую площадь криволинейного треугольника ABC обозначим через S, а его углы (которые, очевидно, являются двугранными углами трехгранного угла OABC ) за φ, ψ, θ. Примените формулу для площади криволинейного треугольника с углами φ, ψ, θ.

Подсказка 3

Примените теорему косинусов для трехгранного угла!

Показать ответ и решение

В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать $∠AOB =α,∠AOC = β,∠BOC = γ.$

Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен $φ.$ Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол $φ.$ Площадь поверхности сферы равна $2 4πR .$ Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно пропорциональна величине $φ$ и равна $2 φ- 2 4πR ⋅2π = 2R φ.$

$PIC$

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на $8$ треугольников. Искомую площадь криволинейного треугольника $ABC$ обозначим через $S,$ а его углы (которые, очевидно, являются двугранными углами трехгранного угла $OABC )$ за $φ,ψ,𝜃.$ Площади криволинейных треугольников, примыкающих к сторонам треугольника $ABC,$ обозначим $Sφ,Sψ,S𝜃.$ С каждым из этих треугольников $ABC$ образует «дольку», поэтому $S +Sφ =2R2φ,S+ Sψ =2R2ψ,S+ S𝜃 = 2R2𝜃.$ Оставшиеся из $4$ -х нерассмотренных криволинейных треугольников симметричны $4$ -м рассмотренным относительно центра сферы. Значит, суммарная площадь рассматриваемых четырех треугольников равна половине площади сферы, то есть $S +Sφ +Sψ +S𝜃 =2πR2.$ Тогда сложим первые три уравнения и воспользуемся четвертым:

2S+ (S +Sφ +Sψ +S𝜃)= 2R2(φ + ψ+ 𝜃)

S = R2⋅(φ+ ψ+ 𝜃− π).

$PIC$

Из теоремы косинусов для трехгранного угла $OABC :$

1 φ= ψ = 𝜃= arccos3.

Отсюда получаем ответ.

$PIC$

Ответ:

$(3⋅arccos1− π)R2 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#71017

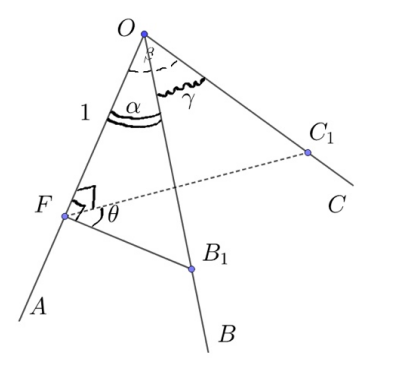
Две сферы касаются друг друга внешним образом и каждая из них касается внутренним образом большей сферы. Радиус одной в два раза, а другой — в три раза меньше радиуса наибольшей сферы. В точке касания малых сфер друг с другом построена касательная плоскость к ним. Найдите расстояние от этой плоскости до центра наибольшей сферы, если ее радиус равен $R.$

Источники: Надежда энергетики-2023, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Не очень удобно работать в пространстве. Может, тогда перейти в плоскость? Давайте перейдем в плоскость α, проходящую через центры наших сфер...

Подсказка 2

Обозначим их центры за O, O₁ и O₂. Пускай R=6r ⇒ радиусы оставшихся двух сфер равны 3r и 2r ⇒ O₁O₂=5r, OO₁=3r и OO₂=4r. Что мы можем сказать про треугольник △O₁OO₂?

Подсказка 3

Верно, он прямоугольный! Пускай плоскость β, касающаяся наших сфер, пересекает α по прямой L. Обозначим за K- точку пересечения OO₂ и L, D- основание перпендикуляра из O на прямую L и F- точку касания маленьких сфер. Какие между собой треугольники △ODK, △KFO₂ и △O₁OO₂?

Подсказка 4

В яблочко, они подобны! Тогда: KO₂/FO₂=O₁O₂/OO₂ ⇒ KO₂=r*5/2 ⇒ KO=r*3/2. Также: OD/KO=OO₂/O₁O₂ ⇒ OD=r*6/5=R/5.

Показать ответ и решение

Проведём сечение описанной композиции плоскостью, проходящей через центры трех сфер. Искомое расстояние будет длиной отрезка $OD$ на этой плоскости.

$PIC$

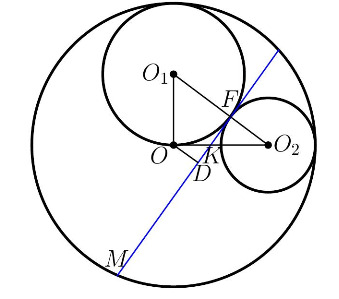
Пусть радиусы малых окружностей равны $2r$ и $3r.$ Тогда радиус наибольшей (внешней) равен $6r$ (дано: $6r= R$ ). Рассмотрим $△O1OO2.$ Его стороны равны $3r,4r$ и $5r,$ следовательно, он прямоугольный.

Обозначим точку пересечения искомой хорды с отрезком $O1O2$ через $F,$ а с отрезком $OO2$ через $K.$ Опустим из центра наибольшей окружности перпендикуляр $OD$ на искомую хорду (отрезок общей касательной). Тогда искомая хорда делится точкой $D$ пополам и перпендикулярна отрезкам $OD$ и $O1O2.$

Прямоугольные треугольники $O1OO2,KFO2,KDO$ подобны. Поэтому $KO O O F-O2= -O1O-2 2 2$ , откуда $5 KO2 = 2r$ и $3 KO = 2r.$

Далее, $OD- OO2-- KO = O1O2,$ откуда $6 1 OD = 5r= 5R.$

Ответ: 0,2 R

Ошибка.
Попробуйте повторить позже

Задача 3#38770

Внутри шара радиуса $R$ взята точка $A$ на расстоянии $a$ от его центра. Через точку $A$ проведены три попарно перпендикулярные хорды. Найдите сумму квадратов длин этих хорд.

Подсказки к задаче

Подсказка 1

Так, три попарно перпендикулярные хорды... Как-то надо применять пространственную теорему Пифагора! Подумайте, чему равна сумма квадратов проекций отрезка AO (где O - центр шара) на оси системы координат (то есть хорды) и на плоскости.

Подсказка 2

Идём в плоскость, в которой проведены наши хорды. Какая теорема про хорду и радиус может нам очень сильно помочь, чтобы выйти на длины хорд?

Подсказка 3

Если радиус перпендикулярен хорде, то этот радиус делит хорду пополам! Тогда мы получили очень много прямых углов в плоскости. Попробуйте записать теорему Пифагора для каждого получившегося прямоугольного треугольника.

Подсказка 4

Теперь осталось вспомнить только то, что радиус окружности, в плоскости которой мы работали, можно найти! А дальше просто подставив его в наше выражение, мы можем выйти на сумму квадратов длин хорд!

Показать ответ и решение

$PIC$

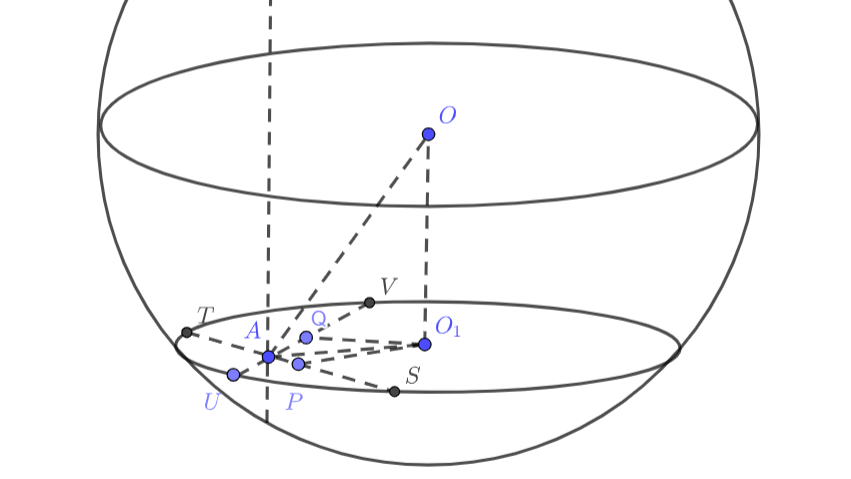
Первое решение.

Рассмотрим сечение шара, которое задаётся двумя пересекающимися в точке $A$ хордами $UV$ и $TS$ . Эта плоскость перпендикулярна каждой из плоскостей, заданных аналогично другими парами хорд, по признаку перпендикулярности плоскостей (каждая из них содержит прямую, перпендикулярную другой плоскости). Тогда они образуют “координатные плоскости” для осей прямоугольной системы координат, направленных вдоль хорд. По пространственной теореме Пифагора сумма квадратов проекций отрезка $AO$ на оси равна квадрату длины отрезка $AO$ , а сумма квадратов проекций отрезка $AO$ на плоскости равна $2AO2 =2a2.$

Итак, рассматриваемое сечение шара является окружностью, обозначим её центр за $O1$ . Известно, что перпендикуляры $O1Q$ и $O1P$ из центра на хорды попадут в середины соответствующих хорд. Если обозначить $x= TS,y = UV$ , то по теореме Пифагора $O1S2 =O1P 2+P S2 = O1P2+ x42,O1V 2 = y42+ O1Q2$ . Заметим, что $O1V2 =O1S2 =r2$ как радиусы окружности. Если сложить равенства, получаем:

2r2 = x2-+y2+ AO2 4 1

Учтём, что $r2 = R2− OO2 1$ . Так как $AO 1$ — проекция $OA$ на плоскость, то складывая аналогичные равенства для двух других координатных плоскостей, получаем

2 2 2x2+-2y2-+2z2 2 2 2 2 2 2 2 2 2 2(3R − a)= 4 + 2a ⇐ ⇒ x + y + z =4(3R − a)− 4a = 12R − 8a

Второе решение.

Рассмотрим прямоугольный параллелепипед, рёбра которого параллельны данным хордам, а точка $A$ и центр $O$ шара являются его противоположными вершинами. Пусть $a1,a2$ и $a3$ - длины его рёбер; ясно, что $2 2 2 2 a1+ a2+ a3 =a$ a) Если хорда удалена на расстояние $x$ от центра шара, то квадрат её длины равен $4R2 − 4x2$ . Так как расстояния от данных хорд до точки $O$ равны диагоналям граней параллелепипеда, то искомая сумма квадратов равна $( ) ( ) ( ) 12R2 − 4 a22+ a23− 4 a21+ a23 − 4 a21+a22 = 12R2− 8a2$

Ответ:

$12R2− 8a2$

Ошибка.
Попробуйте повторить позже

Задача 4#70779

Дана пирамида $PQRS,$ вершина $P$ которой лежит на одной сфере с серединами всех её рёбер, кроме ребра $PQ.$ Известно, что $QR = 2,$ $QS = 1,$ $√- PS = 2.$ Найдите длину ребра $RS.$ Какой наименьший радиус может иметь сфера, описанная около данной пирамиды?

Источники: Физтех-2022, 11.7 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, на что нам могут намекать середины сторон? На средние линии. А средние линии параллельны основаниям. Что мы можем из этого извлечь? Какие параллелограммы есть на картинке?

Подсказка 2

Во-первых, в силу свойства средней линии, ADCE и ABDP - параллелограммы. При этом они вписаны в сечения нашей сферой плоскостей ACD и PRS. А значит, эти параллелограммы - прямоугольники. А это дает много прямых углов, а значит - много перпендикулярностей. Какая прямая тогда перпендикулярна прямой RS? А что нам это дает?

Подсказка 3

Прямая PQ перпендикулярна прямой RS, из за того, что параллельные им прямые EA и AD перпендикулярны. Давайте опустим перпендикуляр QH на RS.

Подсказки 4

Тогда у нас плоскость QHP перпендикулярна RS. Значит, и прямая PH перпендикулярна RS. А значит, наш «согнутый» четырехугольник QRPS (то есть, мы можем повернуть треугольник QRS вокруг RS до момента, когда повернутый треугольник будет лежать в плоскости RPS) имеет взаимноперпендикулярные диагонали. А значит, две суммы квадратов противоположных сторон равны. А тогда мы нашли RP. А значит, у нас фиксированы две стороны прямоугольного треугольника RPS, и мы найдем его гипотенузу.

Подсказка 5

Остается дать оценку на радиус сферы, описанной вокруг тетраэдра. Ну какую самую глупую оценку можно дать? Что первое приходит в голову(с учетом того, что нам еще пример надо построить)?

Подсказка 6

Самая глупая оценка снизу - это то, что радиус не меньше радиуса описанной окружности треугольника QRS. Найти радиус нетрудно(мы знаем все три стороны). Остается привести пример.

Подсказка 7

Чтобы достигалось равенство, надо, чтобы у нас в плоскости QRS лежал содержался центр сферы. Впишем туда треугольник QRS.

Подсказка 8

Остается доказать, что на сфере найдется точка P’, такая, что треугольники PRS и P’RS равны(это по сути и значит, что получен тетраэдр, который подходит под условия). То есть по сути надо поворачивать треугольник P’RS, равный треугольнику PRS, вокруг RS, до того момента, как точка P’ не станет принадлежать окружности.

Показать ответ и решение

Пусть $A,B,C,D,E$ - середины рёбер $PR,RS,QS,PS,QR$ соответственно. Из теоремы о средней линии треугольника следует, что $ADCE$ и $ABDP$ - параллелограммы. Они вписаны в окружности, являющиеся сечениями сферы плоскостями $ACD$ и $PRS$ , поэтому эти параллелограммы - прямоугольники. Угол $RP S$ — прямой; прямые $PQ$ и $RS$ перпендикулярны, так как $P Q∥AE, AE ⊥CE, CE ∥RS.$

Отметим в плоскости $PRS$ точку $′ Q$ такую, что $′ △QRS = △Q RS,$ а точки $P$ и $′ Q$ лежат по разные стороны от прямой $RS$ (треугольник $′ QRS$ может быть получен из треугольника $QRS$ поворотом вокруг прямой $RS).$

$PIC$

Из равенства треугольников $QRS$ и $Q′RS$ следует, что основания их высот, опущенных на $RS$ — это одна и та же точка (назовём её $H ).$ Плоскость $HQQ ′$ перпендикулярна $RS$ (так как $QH ⊥ RS,Q′H ⊥ RS),$ поэтому $QQ′ ⊥ RS.$ Поскольку $QQ ′ ⊥ RS$ и $PQ ⊥ RS,$ то плоскость $P QQ′$ перпендикулярна $RS$ и $PQ ′ ⊥RS.$

Значит, диагонали четырёхугольника $PRQ ′S$ пересекаются под прямым углом (в точке $H$ ). По теореме Пифагора

PR2 =P H2+ RH2,Q′R2 = Q′H2+ RH2,

Q′S2 =Q ′H2 +SH2,P S2 = PH2+ SH2

Следовательно,

P S2+ Q′R2 = PR2+ Q′S2

∘------------- PR = 22+ (√2)2− 12 = √5

Из прямоугольного треугольника $PRS$ находим

∘---2----2 √- RS = PR +P S = 7

Радиус сферы, описанной около пирамиды $PQRS$ , не меньше радиуса $r$ окружности, описанной около грани $QRS$ . Пирамида, для которой достигается равенство, существует. Докажем это.

$PIC$

Рассмотрим сферу радиуса $r$ и окружность - её сечение, проходящее через центр сферы. В сечении сферы указанной плоскостью получится окружность с диаметром $RS$ , в которую можно вписать прямоугольный треугольник $PRS$ . По теореме косинусов из треугольника $PRS$ находим, что

QR2+ QS2− RS2 4+1 − 7 1 cos∠RQS = --2⋅QR-⋅QS----= 2-⋅2-⋅1--=− 2

∠RQS =120∘

По теореме синусов

RS √7- r = 2sin∠RQS-= √3-

Ответ:

$RS = √7,R =∘ 7- min 3$

Ошибка.
Попробуйте повторить позже

Задача 5#71956

В пирамиде $SA A ...A 1 2 n$ все боковые рёбра равны. Точка $X 1$ — середина дуги $A A 1 2$ описанной окружности треугольника $SA A , 1 2$ точка $X2$ — середина дуги $A2A3$ описанной окружности треугольника $SA2A3$ и т. д., точка $Xn$ — середина дуги $AnA1$ описанной окружности треугольника $SAnA1.$ Докажите, что описанные окружности треугольников $X1A2X2,X2A3X3,...,XnA1X1$ пересекаются в одной точке.

$PIC$

Источники: СпбОШ - 2021, задача 11.3(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1:

Давайте поймем, поизучаем сферу, описанную вокруг данной фигуры. Во-первых, почему вообще можно описать сферу? Во-вторых, где у неё центр?

Подсказка 2:

Вокруг многоугольника A₁A₂...Aₙ можно описать окружность, значит, вокруг всей фигуры можно описать сферу. Пусть центр сферы — это точка P. Она равноудалена от точек A, следовательно, лежит на прямой, перпендикулярной плоскости основания и проходящей через S. Что мы можем сказать про точки X? Где они лежат?

Подсказка 3:

Они тоже лежат на этой сфере! Давайте попробуем угадать, где может находиться искомая точка. Попробуйте нарисовать фигуру и провести окружности.

Подсказка 4:

Давайте попробуем доказать, что искомая точка пересечения диаметрально противоположна S. Тогда нужно доказать, что N, X(k−1), X(k) и A(k) лежат на одной плоскости. Как это можно сделать?

Подсказка 5:

Воспользуемся тем, что N диаметрально противоположна S. Тогда угол SA(k)N прямой при всех A(k). Какие ещё углы равны 90 градусам?

Подсказка 6:

Углы SA(k)X(k) прямые, потому что S и X(k) диаметрально противоположны в окружности, описанной вокруг треугольника SA(k)X(k). Тогда SA перпендикулярно какой плоскости? Какие точки на ней лежат?

Показать доказательство

Заметим, что точки $A ,A ,...,A 1 2 n$ лежат и на сфере с центром в точке $S,$ и в одной плоскости. Следовательно, они лежат на окружности $ω,$ являющейся пересечением сферы с плоскостью. Пусть $O$ — центр этой окружности. Тогда $SO$ перпендикулярно плоскости основания и любая точка на прямой $SO$ равноудалена от всех точек окружности $ω.$ Поэтому на $SO$ найдётся и такая точка $P,$ для которой $P S = PA1.$ Тогда на сфере $σ$ с центром в точке $P$ и радиусом $PS$ лежат все вершины пирамиды, а также все окружности $SAkAk+1.$

$PIC$

Следовательно, на этой сфере лежат все точки $Ak$ и $Xk.$ Пусть $N$ — точка на сфере $σ,$ диаметрально противоположная точке $S.$ Покажем, что описанные окружности треугольников $Xk− 1AkXk$ проходят через точку $N.$ Поскольку точки $N, Xk−1,Xk$ и $Ak$ лежат на сфере, достаточно проверить, что они лежат на сфере, достаточно в одной плоскости. Эта плоскость перпендикулярна прямой $SAk$ и проходит через точку $Ak.$ В самом деле, $∠SAkN = 90∘,$ поскольку они опирается на диаметр $SN$ сферы $σ,∠SAkXk =90∘$ и $∠SAkXk −1 = 90∘,$ поскольку они опираются на диаметры $SXk$ и $SXk −1$ описанных окружностей треугольников $SAkXk$ и $SAkXk −1.$

Ошибка.
Попробуйте повторить позже

Задача 6#63898

Двугранный угол при основании правильной треугольной пирамиды $SABC$ равен $arctg3.$ В каком отношении делит боковую сторону $SB$ сфера, центр которой лежит в плоскости основания, если известно, что вершины основания принадлежат сфере?

Подсказки к задаче

Подсказка 1

Центр сферы лежит в плоскости основания и при этом сфера проходит через все вершины правильного треугольника основания. Что в таком случае можно сказать о положении центра сферы внутри △ABC?

Подсказка 2

Итак, мы поняли, что центр сферы совпадает с центром △ABC. Из этого мы сразу же можем узнать радиус сферы. Обозначьте сторону основания пирамиды за переменную а и попробуйте через неё выразить всё что сможете: радиус сферы, высоту пирамиды (в этом нам поможет двугранный угол при основании).

Подсказка 3

Обозначим центр сферы за точку О и рассмотрим △SOB, все его стороны легко выражаются через а. Из точки О проведите ОР — радиус сферы. Работа с равнобедренным △ВОР (мы знаем в нём боковые стороны и можем выразить из прямоугольного △SOB угол при основании) поможет нам отыскать ВР. Осталось несколько арифметических действий и задача решена!

Показать ответ и решение

$PIC$

Центр сферы равноудалён от точек на её поверхности, а раз по условию вершины основания принадлежат сфере, то центр сферы является центром описанной около основания окружности.

Пусть сфера пересекает ребро $SB$ в точке $P$ . Тогда равны радиусы $OP =OB.$ Опустим перпендикуляр $OQ$ к ребру $SB$ , он является медианой равнобедренного треугольника $P OB.$ Обозначим сторону основания через $a$ и пусть угол $α =arctg3.$ Пусть $M −$ основание перпендикуляра, проведенного из точки $B$ на сторону $AC.$

Находим из правильного треугольника в основании $√- √ - OM = 13a23,OB = 23a23$ , а так как $∠SMO$ это линейный угол двугранного угла и равен $α$ , то $√- SO = a63tgα.$

Также заметим

cos∠SBO = BQ- = BO BO SB

Тогда получаем

BQ- BO2- 2 -----1----- SB = SB2 = cos ∠SBO = 1+ tg2 ∠SBO =

(так как $√- a√3- tgα tg∠SBO =a 36tgα :-3-= -2-)$

1 4 4 = ---tg2α-= 4+tg2α-= 13- 1+ 4

В итоге $BQ =QP = 4x,SB = 13x,$ так что сфера делит в отношении

SP-= 13x−-8x= 5 PB 8x 8

Ответ:

$5 :8$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#63893

Отрезок $AB = 8$ пересекает плоскость $α$ под углом $30∘$ и делится этой плоскостью в отношении $1:3$ . Найдите радиус сферы, проходящей через точки $A$ и $B$ и пересекающей плоскость $α$ по окружности наименьшего радиуса.

Источники: Ломоносов-2015, 11.5 (см. olymp.msu.ru)

Показать ответ и решение

Обозначив точку пересечения $AB$ с плоскостью $α$ через $C$ , получим $AC =2,BC = 6$ . В пересечении сферы с плоскостью получается некоторая окружность. Проведём через $C$ диаметр $MN$ этой окружности.

$PIC$

Тогда $AB$ и $MN$ — хорды сферы, и по свойству пересекающихся хорд: $MC ⋅CN = AC ⋅CB = 12$ . Так как $------- - MN = MC + CN ≥2√MC ⋅CN =4√ 3$ , то минимальный радиус окружности больше или равен $- 2√3$ и значение $- 2√ 3$ достигается при $MC =CN =2√3$ , то есть $C−$ центр этой окружности. Так как $∠COP = 90∘− ∠OCP = ∠NCP = 30∘$ , то $OC =2⋅CP.$ При этом $CP = AB2-− AC = 2.$ Значит, $R2 =OM2 =MC2 + OC2 = 12 +42 = 28.$

Ответ:

$2√7$

Ошибка.
Попробуйте повторить позже

Задача 8#63895

В правильную треугольную призму $ABCA B C 1 1 1$ вписан шар радиуса $√2$ . Найдите площадь боковой поверхности вписанного в шар прямого кругового цилиндра, основание которого лежит в плоскости, проходящей через точку $A$ и середины рёбер $BB1$ и $CC1.$

Источники: Ломоносов-2014, 11.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте аккуратно нарисуем рисунок, попробуем выразить радиус основания цилиндра через его высоту и радиус сферы. Обозначим за D, D₁, M и N середины ребер ВС, В₁С₁, ВВ₁ и СС₁, Р – точка пересечения MN и DD₁. Как имеющиеся на рисунке отрезки связаны с радиусом сферы?

Подсказка 2

Давайте спроецируем центр сферы на плоскость основания цилиндра, нельзя ли теперь выделить на рисунке какую-нибудь пару подобных треугольников, которая поможет нам связать высоту цилиндра и радиус сферы?

Показать ответ и решение

Обозначим через $r$ радиус шара, а через $D,D ,M 1$ и $N$ — середины рёбер $BC,B C ,BB 11 1$ и $CC 1$ соответственно. Плоскость $AA D 1 1$ есть центральное сечение шара. Пусть $h$ — высота цилиндра, тогда радиус его основания равен $∘-2--h2 R = r − 4$ . Пусть $P$ — точка пересечения отрезков $DD1$ и $MN$ . Справедливы соотношения $OP = r,P D= r,AD =3r$ , где $O−$ центр шара. Если $O1$ — проекция точки $O$ на основание цилиндра, то из подобия прямоугольных треугольников $APD$ и $OO1P$ получаем