.09 Механика вращательного движения

Поскольку на стержень действуют тела и ось вращения, и сумма этих сил равна нулю, то для нахождения силы, действующей со стороны стержня на ось вращения, найдём силу, с которой на стержень действуют тела. А для этого, рассматривая движение тел, найдём силу, с которой стержень действует на тела.

После отпускания стержня оба тела будут двигаться по окружностям. Поэтому их ускорения имеют и нормальную, и тангенциальную компоненты. Но т.к. сразу после отпускания у тел практически нулевая скорость, их ускорения в этот момент направлены по касательным к траекториям. Т.е. вектор ускорения тела направлен вертикально (вниз), тела — горизонтально (направо). Поэтому силы и , действующие на тела со стороны стержня, направлены так, как показано на рисунке — сила направлена вертикально, сила имеет и вертикальную, и горизонтальную составляющие.

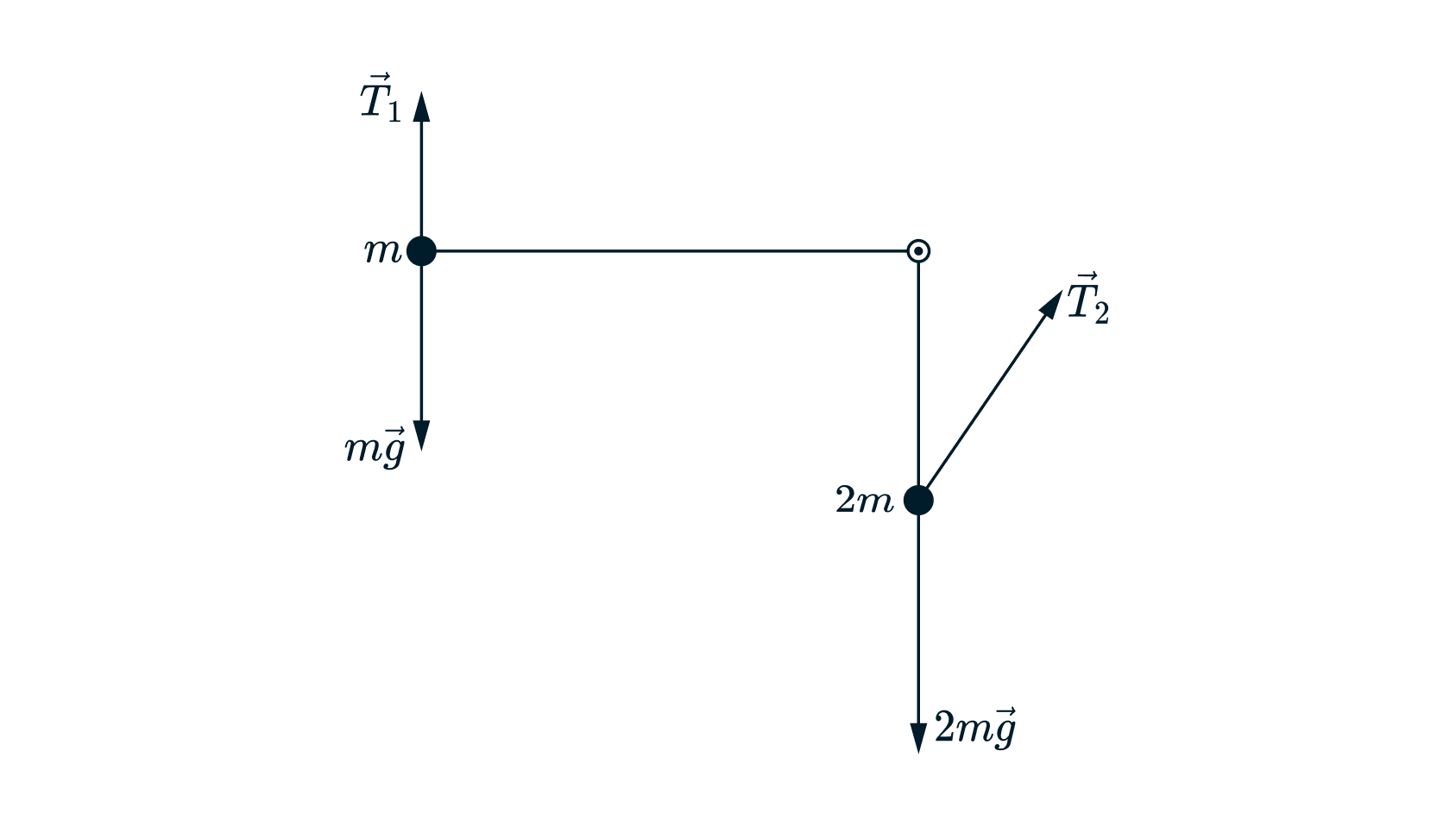
Второй закон Ньютона для тел в проекциях на вертикальную ось (для первого тела) и вертикальную () и горизонтальную () оси для второго тела:

Стержень невесомый, поэтому сумма сил и сумма моментов всех сил, действующих на него, должны равняться нулю. Нулевая сумма сил получится всегда из-за силы, действующей на оси, а вот нулевая сумма моментов должна получаться для наших сил. Поэтому:

Так как наша конструкция является жёсткой, она вращается вокруг оси как целое. Поэтому в любой момент времени линейная скорость тела массой вдвое больше линейной скорости тела с массой . Поэтому:

Решая систему уравнений с этими условиями, получим:

Отсюда следует, что со стороны тел на стержень действует сила с горизонтальной составляющей и вертикальной составляющей

Суммарная сила:

А поскольку сумма сил, действующих на стержень, должна равняться нулю, то именно с такой силой ось вращения действует на стержень, а стержень — на ось вращения.