Муниципалка 8 - 9 класс
Ошибка.
Попробуйте повторить позже
В равнобедренном прямоугольном треугольнике угол
равен
, точка
середина
Прямая, проходящая через точку
и перпендикулярная
, пересекает сторону
в точке
. Докажите, что
.
Подсказка 1
Нам дали в задаче хорошую фигуру, но давайте её ещё "улучшим", чтобы связать отрезки на картинке или получить более удобную конструкцию. Тогда до какой фигуры логично достроить нашу картинку?
Подсказка 2
Да, конечно же до квадрата, и, чтобы точно на картинке всё было связано, продлим AP до пересечения со стороной квадрата в точке N. У нас достаточно много прямых уголков образовалось, четырёхугольников и прямоугольных треугольников. Нельзя ли что-то понять про один из четырёхугольников?
Подсказка 3
Верно, один из них является вписанным, а значит углы AMC и ABN равны. Тогда, если эти два угла равны PMB, то становится понятно, что же нам в итоге надо доказать. Равенство треугольников PMB и PNB. Получается для этого нам не хватает только равенства MB и BN. Как это можно доказать? Может быть стоит воспользоваться какими-то двумя другими треугольниками для этого.
Подсказка 4
Верно, можно сказать, что треугольники ACM и ABN равны по катету(стороне квадрата) и острому углу. Откуда и получаем равенство сторон, а значит, как мы поняли до этого, решаем задачу. Победа!
Достроим равнобедренный прямоугольный треугольник до квадрата
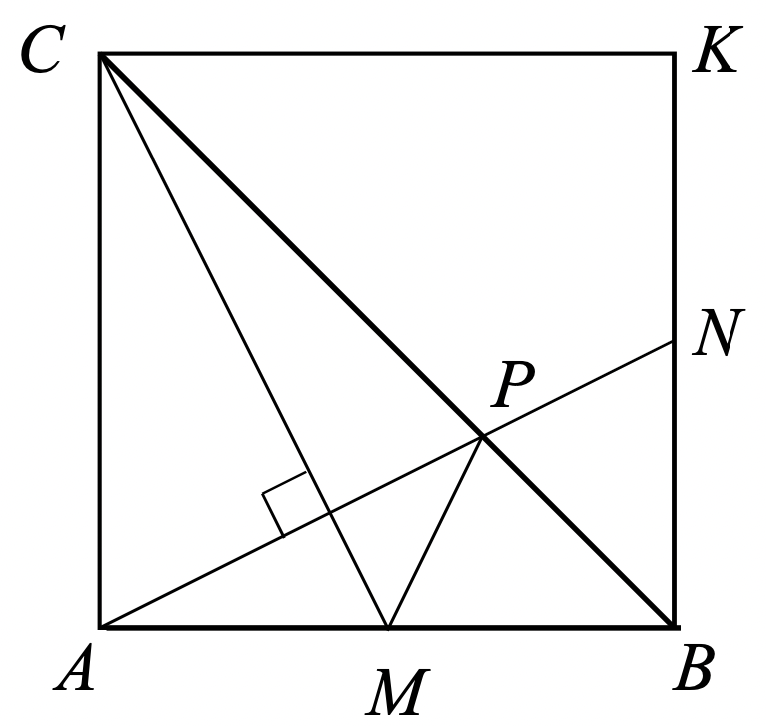
Пусть — точка пересечения
и
Прямые
и
взаимно перпендикулярны, поэтому
Отсюда
следует равенство прямоугольных треугольников
и
, и значит,
Так как
и
, то
треугольники
и
равны по двум сторонам и углу между ними. Следовательно,
и так как
, требуемое равенство доказано.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




