Тема . Механика. Динамика и Статика

.08 Метод виртуальных перемещений

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела механика. динамика и статика

Решаем задачу:

Ошибка.
Попробуйте повторить позже

Задача 1#124650

Космическая станция, расположенная на геостационарной орбите, имеет форму цилиндра длины $L = 100$ км и радиуса $R = 1$ км. Станция заполнена воздухом (его молярная масса $M = 29$ г/моль) при атмосферном давлении и температуре $T = 295$ К. Цилиндрическая поверхность служит «полом» для обитателей станции. Станция вращается вокруг своей оси, и создает привычное ускорение свободного падения $g = 9.81$ м $2 ∕c$ на «полу».
1. Чему равен период вращения $τ$ ?
2. Мяч бросают из некоторой точки на «полу», а затем, спустя $t = τ∕2$ , ловят его в той же самой точке. С какой скоростью бросали мяч? Сопротивлением воздуха пренебречь.
3. Воздушный шарик радиуса $r = 3$ м наполнили гелием (молярная масса гелия $M ′ = 4$ г/моль). Шарик используют чтобы поднять груз неизвестной массы $m$ . Груз прикрепили к шарику легкой веревкой длины $L = 20$ м. Эта конструкция поднимается и в конце концов останавливается на высоте $H = 500$ м от «пола». Определите значение массы $m$ . Веревка (ее линейная плотность $λ = 1$ кг/м) прикреплена к «полу»в двух диаметрально противоположных точках цилиндра (так, что расстояние между ее концами равно $2R$ ). Пусть точки $A,B$ и $C$ - это два конца веревки и ее середина соответственно.
4. Пусть точка $C$ расположена на высоте $h$ над «полом». Найдите $TA − TC$ , разность сил натяжения веревки в точках $A$ и $C$ .
5. Пусть в точке $A$ угол, который составляет веревка с «полом» равен $α$ . Найдите отношение сил натяжения $TA∕TC$ .
6. Аппроксимируя форму веревки параболой, найдите $TC$ , если $h = 495$ м.
(NBPhO, 2024)

Показать ответ и решение

Решение
1. Обозначим угловую скорость вращения за $ω$ , тогда на полу станции центробежная сила $mω2R = mg$ . Тогда с учетом $ω τ = 2π$ :

( )2 2π- R = g τ

∘ -- τ = 2π R- g

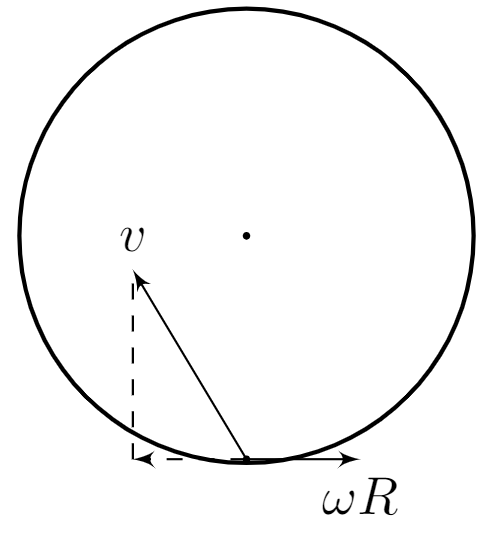
2. В лабораторной системе отсчета (ЛСО) шарик будет двигаться по прямой. В этой системе отсчета за время $t$ станция повернется на угол $π$ , значит шарик должен лететь вдоль диаметра со скоростью $2R- 4R- t = τ$ . Скорость шарика в ЛСО складывается из скорости $ωR = 2πR- τ$ , скоторой двигается пол станции, и скорости броска $v$ . Тогда

∘ ----------------- ( 4R )2 ( 2πR )2 v = -τ- + -τ--

Преобразовав и подставив цифры, имеем:

2R-∘ ----2- v = τ 4+ π = 117m∕c

3. На воздушный шарик действует сила инерции и сила Архимеда со стороны воздуха $4πr3(ρB − ρr)⋅ω2(R − H ) 3$ . Эта сила уравновешена силой инерции действующей на груз $mω2(R − H + l)$ . В таком случае мы имеем уравнение:

4 3 2 2 3πr (ρB − ρr) ⋅ω (R − H ) = m ω (R − H + l) (1)

При расчете плотности газов $ρ$ будем пренебрегать эффектами связанными с зависимостью давления воздуха от высоты. Из уравнения Менделеева-Клапейрона получим:

m pM pV = νRgT ⇒ pV = --RgT ⇒ ρ = ---- M RgT

Подставляя плотности газов в уравнение (1), и выражая оттуда массу, имеем:

m = 4π-pr3--R-−-H---(M − M ′) 3 RgT R − H + l

4. Действие центробежной силы на тело эквивалентно нахождению в осесимметричном потенциале

∫ r( ) ω2r2 φ(r) = − ωx2 dx = −---- 0 2

При решении этого пункта удобно использовать принцип виртуальных перемещений для веревки. Вытянем ее конец $A$ на малую длину $dl$ вдоль направления силы $TA$ , тогда работа сил натяжения равна $dl(TA − TC)$ , а изменение энергии веревки в поле $φ(r)$ равно $dlλ(φ (R )− φ(R − h))$ . Значит

R2 − (R− h)2 TA − TC = − λω2----------- 2

Учитывая, что $ω = 2π- τ$ и раскрывая квадрат разности имеем:

TA − TC = − 2π2λh(2R-−-h) τ2

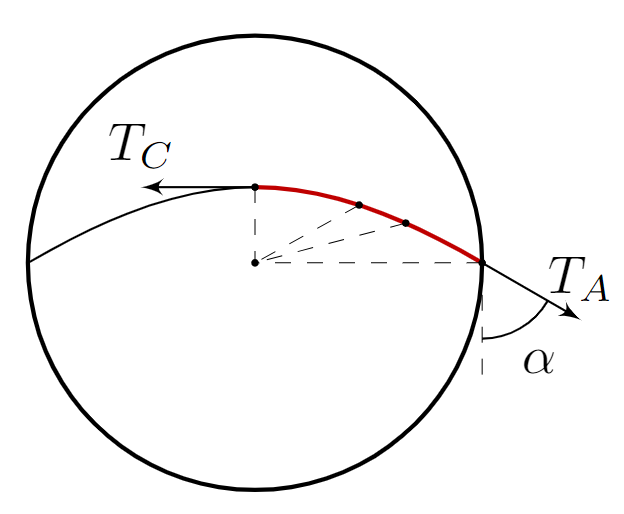
5. На единицу длины веревки действует сила инерции направленная из центра станции $O$ . Тогда относительно точки $O$ уравнение моментов на часть веревки, лежащую между точками $A$ и $C$ выглядит так:

TAR cosα = TC(R − h)

TA- R-−-h- TB = Rcosα

6. Аппроксимируя форму веревки параболой $y(x) = βx2$ , найдем $β$ из условия $R − h = y(R ) = βR2$ . Тогда $′ tan α = y (R) = 2βR$ , значит

cosα = ∘--2βR-----= ∘-----1------- 1 + 4β2R2 R2 1+ 4(R-−-h)2

Этот результат позволяет разрешить систему уравнений, полученных в пунктах (4) и (5):

( |{ T − T = − 2π2λh(2R-−-h) A C τ2 |( TA-= -R-−-h TC R cosα

Решая систему, получим:

2 --(---λh-(2R-−-h)-----)-- 3 TC = 2π = 12.6⋅10 H || || τ2||1 − ∘-----1-------|| ( ---R2----) 1+ 4(R − h)2

Ответ:

$∘ R- 1.τ = 2π g-$
$2R √------ 2.v = -τ- 4 + π2 = 117m ∕c$
$4π pr3 R − H ′ 3.m = 3-RgT- R−-H-+-l-(M − M )$
$λh(2R− h) 4.TA − TC = − 2π2---τ-2----$
$TA- -R−-h- 5. TB = R cosα$
$2-------λh(2R-−-h)------- 3 6.TC = 2π ( ) = 12.6⋅10 H || || τ 2||1 − ∘-----1-------|| ( ---R2----) 1+ 4(R − h)2$

Нужна консультация? Задайте нам вопрос в чате.

Специальные программы

Все специальные программы

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

.08 Метод виртуальных перемещений

Специальные программы

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ