.01 Гидростатика
Ошибка.
Попробуйте повторить позже
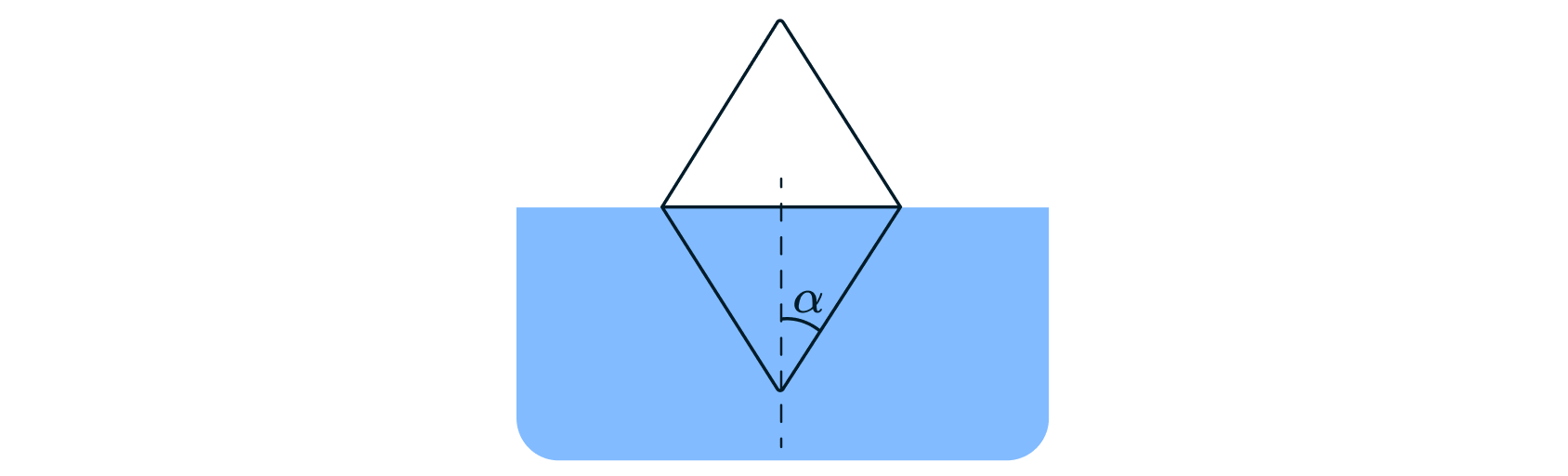
Буй составлен из двух одинаковых металлических конусов с высотой и углом при вершине
(см.
рисунок). Буй плавает в воде в вертикальном положении, погрузившись в воду до половины. Через щели
внутрь буя просачивается вода, выходит воздух, и буй медленно погружается в воду. Будет ли меняться
разность уровней воды внутри и снаружи буя в процессе его погружения в воду? Найти разность уровней
воды внутри и снаружи буя в тот момент времени, когда она будет минимальной. Толщиной стенок буя
пренебречь.
Указание. Объём прямого кругового конуса определяется соотношением , где
— радиус основания конуса,
— его высота.
Источники:
.png)
Пусть в буй просочилась вода, и он погрузился на некоторую глубину (см. рисунок). Рассмотрим условие равновесия буя. В равновесии сила тяжести равна силе Архимеда. Поэтому
где - масса буя,
- масса воды в буе,
- плотность воды,
объем погруженной в воду
части буя. С другой стороны, объем погруженной в воду части буя складывается из (стенки буя считаем
тонкими) объема его погруженной части, заполненной водой
, и объема его погруженной части
без воды
. Поэтому
Но в пренебрежении толщиной стенок, очевидно, . Поэтому условие равновесия буя
дает
Из этой формулы следует, что объем его подводной части, не заполненный водой, определяется
только массой самого буя, т.е. не меняется в процессе его погружения в воду из-за наполнения водой. А
поскольку ширина центральной части буя больше ширины его концов, то расстояние между уровнем
воды внутри буя и уровнем воды в водоеме будет максимальным, когда максимальна ширина части
буя, расположенной между этими уровнями. Т.е. это расстояние будет минимально, если
расстояния от середины буя до уровня воды внутри буя и уровня воды в водоеме будут
одинаковы (см. рисунок, эти расстояния обозначены как ). Найдем эти расстояния. Из
условия равновесия буя без воды (учитывая, что он погружается в воду ровно наполовину)
имеем
.png)
где - радиус самой широкой части буя. Если буй заполнен водой слоем высотой
, то
объем незаполненной водой части буя от его средней части до уровня воды внутри буя будет
равен
Поскольку в случае минимального расстояния между уровнями воды внутри буя и в водоеме
расстояния от средней части буя до уровней воды внутри буя и в водоеме одинаковы, объем
незаполненной водой подводной части буя равен удвоенному объему и равен объему половины буя.
Поэтому
Отсюда находим
А минимальное расстояние между уровнями воды внутри буя и в водоеме равно
(Официальное решение Росатом)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




