.01 Гидростатика
Ошибка.
Попробуйте повторить позже
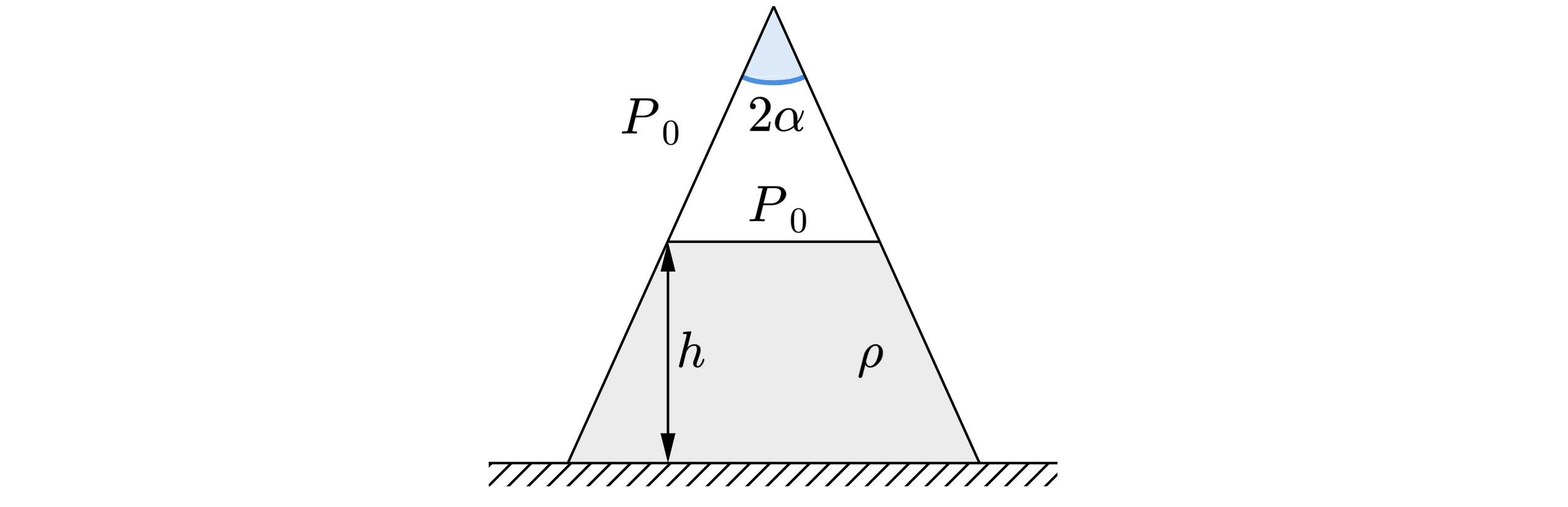
Полая прямая призма, сделанная из тонкого прочного листового материала, имеет высоту , а её основания
представляют собой равнобедренные треугольники с углом
между боковыми сторонами. У призмы аккуратно удалили
боковую грань, лежащую напротив угла
, и поставили призму на гладкий стол так, что упомянутый угол оказался
сверху (основание призмы лежит в плоскости рисунка, её высота перпендикулярна плоскости рисунка). Вблизи
оказавшегося сверху угла проделали маленькое отверстие, и начали медленно заливать через него внутрь призмы воду
плотностью
. В момент, когда уровень воды в призме достиг высоты
, вода начала вытекать из-под призмы. Найдите
массу
призмы с удалённой гранью, считая, что давление
воздуха над водой в призме и снаружи одинаково и равно
атмосферному.
(«Курчатов», 2015, 9, 11)
Источники:
Силу тяжести, действующую на сосуд, должна уравновешивать сила давления на стенки сосуда со стороны воды. Найдём
модуль силы давления , действующей на часть одной из стенок сосуда малой высотой
, находящуюся на глубине
(см. рис.):
.png)
Проекция этой силы на вертикальную ось равна
Чтобы найти проекцию полной силы, действующей на стенку, нужно просуммировать проекции
сил, действующих на все участки, лежащие на глубинах от 0 до
. Это всё равно, что найти площадь под
графиком зависимости
от
. Поскольку этот график линейный с угловым коэффициентом
,
то
Осталось учесть, что у сосуда есть две стенки, и приравнять нулю сумму силы тяжести и проекции силы
давления
:
(Официальное решение Курчатов)
| Критерии оценивания выполнения задачи | Баллы |
| Найдена сила давления, действующая на малый участок стенки | 3 |
| Найдена полная сила давления | 3 |
| Получен ответ | 4 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




