.01 Гидростатика
Ошибка.
Попробуйте повторить позже
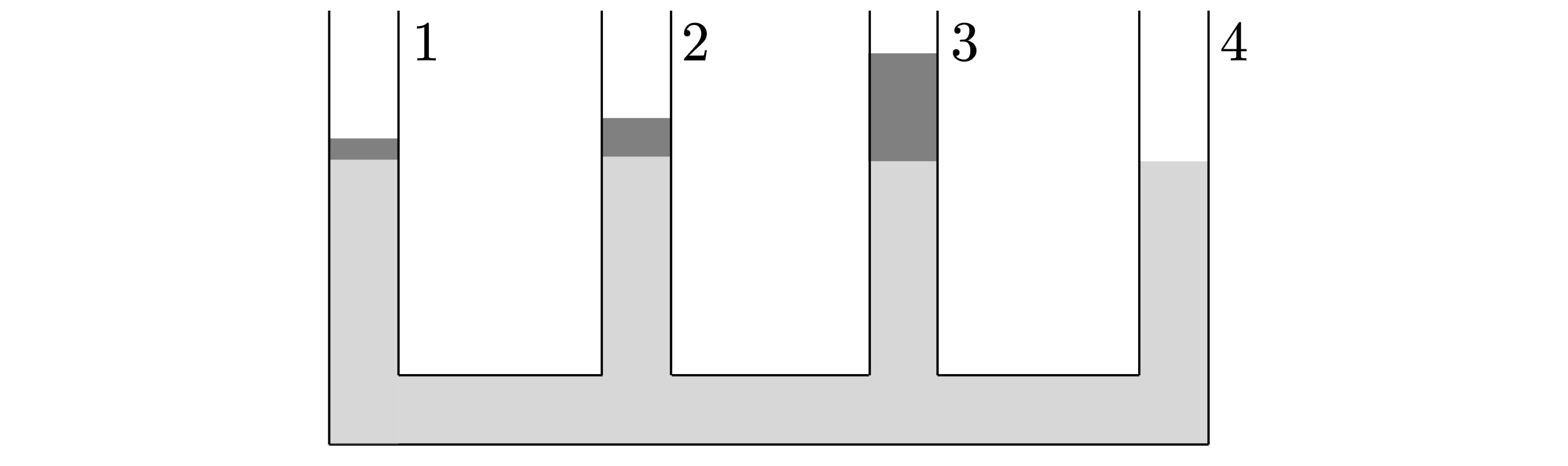
Имеются четыре одинаковых цилиндрических сосуда, в которые налито некоторое количество воды. Поверх воды в
первый, второй и третий сосуды (сосуды перенумерованы на рисунке) аккуратно наливают слой масла толщиной
соответственно ,
и
. На сколько изменится уровень жидкости в каждом сосуде по сравнению с первоначальным
положением после установления равновесия? Известно, что при наливании масла вода ни из одного сосуда полностью
маслом не вытесняется. Плотность масла
, воды —
(
).
(«Росатом», 2017, 10–11)
Источники:
С точки зрения давления в жидкости наливание в сосуд слоя масла толщиной эквивалентно наливанию слоя воды
толщиной
Поэтому наливание в систему сосудов слоя масла толщиной (в первый, второй и третий сосуды) эквивалентно тому,
что мы нальем слой воды толщиной
Но если бы мы налили такое количество воды, она распределилась бы равномерно по четырем сосудам. Учитывая, что в четвертом сосуде будет только вода (по условию масло полностью воду ни из одного сосуда не вытесняет и, следовательно, не может попасть в четвертый сосуд), то уровень воды в нем поднимется на величину
При этом давление в жидкости (около дна сосуда) возрастет на величину
Изменение уровня жидкости в первом, втором и третьем сосудах найдем из условия увеличения давления в этих сосудах на эту величину.
В первом сосуде находится слой масла толщиной , который обеспечивает дополнительное давление
. Поэтому
для увеличения давления на
в левый сосуд должна войти дополнительная вода, дающая давление около дна
cocyда
, т.е. слой воды толщиной
. Это значит, что уровень жидкости в перовом сосуде
увеличится на величину
Во втором сосуде появится дополнительный слой масла толщиной , который обеспечивает дополнительное
давление
Поэтому чтобы давление около дна второго сосуда возросло на величину из второго сосуда должна уйти вода
толщиной
. Поэтому уровень воды во втором сосуде поднимется на величину
В третьем сосуде появится дополнительный слой масла толщиной , который обеспечивает дополнительное
давление
Поэтому чтобы давление около дна третьего сосуда возросло на величину из третьего сосуда должна уйти вода
толщиной
. Поэтому уровень воды в третьем сосуде поднимется на величину
(проверка: сумма подъемов уровней жидкости во всех сосудах должна дать то, что налили, т.е. .
как и должно быть).
(Официальное решение Росатом)
| Критерии оценивания выполнения задачи | Баллы |
| Формула связи высот жидкостей | 2 |
| Формула гидростатического давления | 2 |
| Формула общей высоты жидкости | 2 |
| Выражена искомая величина | 2 |
| Представлен правильный ответ | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




