МКТ. Влажность
Ошибка.
Попробуйте повторить позже
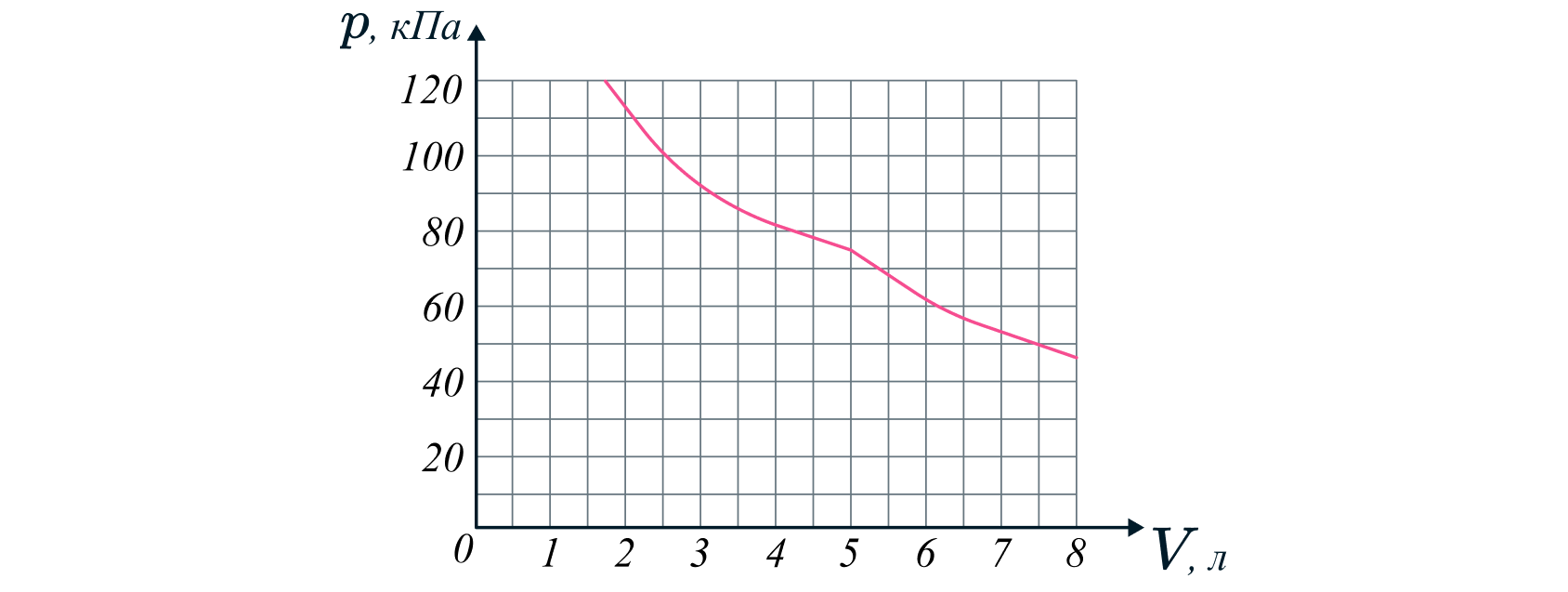
В цилиндре под поршнем находится смесь воздуха и паров некоторой жидкости. Смесь изотермически
сжимают. На рисунке представлена экспериментальная зависимость давления в сосуде от объёма в этом
процессе. Чему равны давление насыщенных паров жидкости при данной температуре и внутренняя
энергия смеси при объёме цилиндра более 5 л?
Примечание. Считать воздух идеальным двухатомным газом, а пары жидкости — идеальным трёхатомным газом.
(Всеросс., 2008, финал, 10)
Предположим, что эксперимент проводится при температуре . Очевидно, что насыщение пара
наступает в точке излома изотермы. Тогда для объёмов
л уравнение газового состояния в
соответствии с законом Дальтона имеет вид:
где количество молей воздуха в сосуде, а
количество молей паров жидкости в сосуде,
любой объём, превышающий 5 л, а
соответствующее ему давление в сосуде (рис.
1).
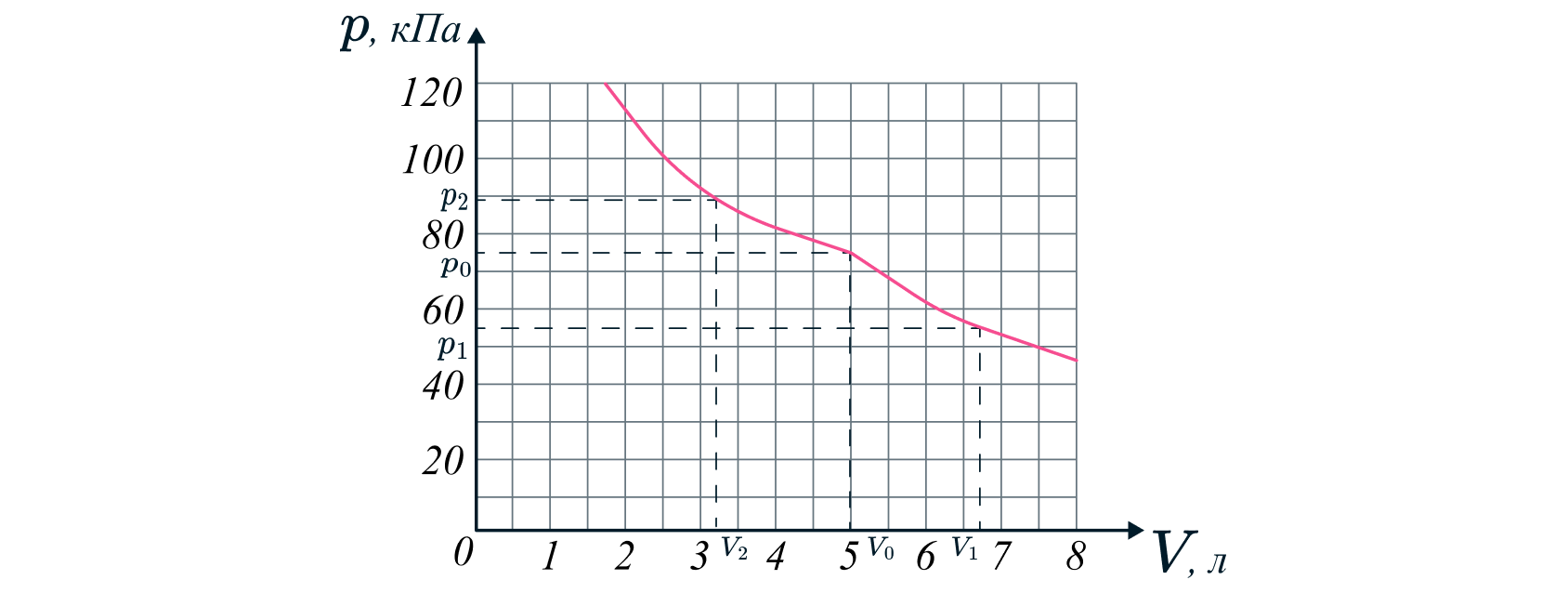
Для объёмов л давление в сосуде складывается из давления воздуха и давления насыщенного
пара. Уравнение газового состояния имеет вид:
где - любой объём, не превышающий 5 л. Изотермы (1) и (2) пересекаются в точке
,
следовательно, при
имеем :
Подставляя (2) и (3) в (1) и решая полученное уравнение относительно , находим
:
Следует заметить, что для получения более точного численного результата целесообразно с помощью
графика на рисунке 27 вычислить несколько произведений для различных объемов
л и
усреднить полученные значения. Аналогичным образом, вычисление окончательного результата с
помощью выражения (6) следует проводить для нескольких значений
и соответствующих ему
значений
. При построении графика использовались численные значения:
молей,
молей,
кПа. Внутренняя энергия смеси при
л вычисляется по
формуле:
С учётом выражений (5) и (6) форм ула приобретает вид:
(Официальное решение ВсОШ)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




