.19 Теорема Кёнига
Ошибка.
Попробуйте повторить позже
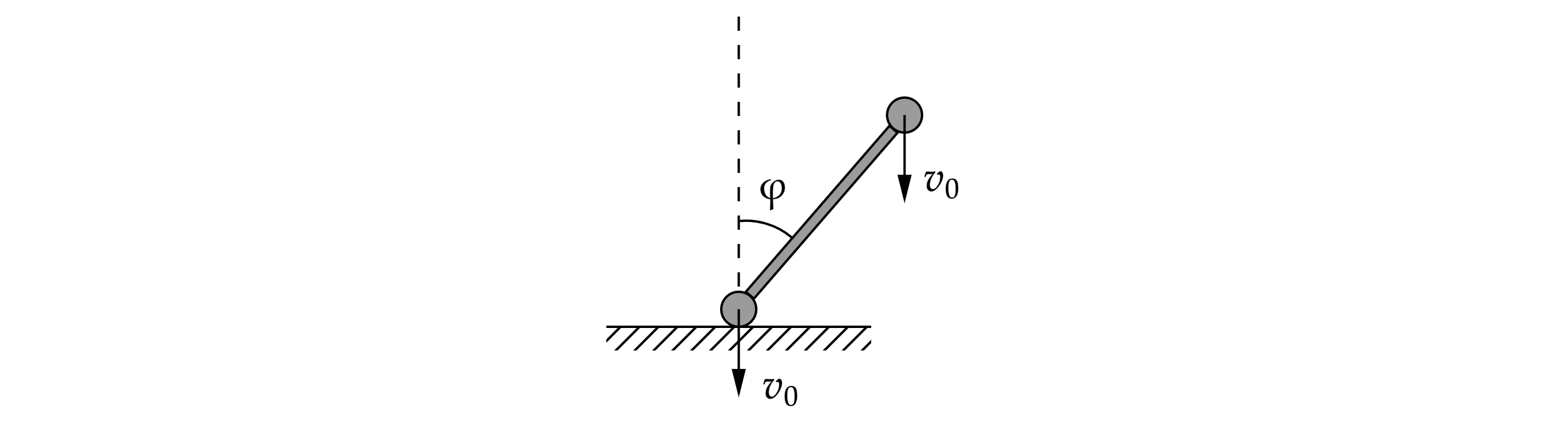
Два одинаковых маленьких шарика, соединённых невесомым твёрдым стержнем длины , падают на гладкую, абсолютно
упругую горизонтальную плоскость. Непосредственно перед ударом нижнего шарика о плоскость скорости
шариков направлены вертикально вниз и равны
, а сразу после удара скорости шариков оказались взаимно
перпендикулярны.
1) Каковы величина скорости центра масс гантели и угловая скорость вращения стержня
сразу после
удара?
2) Под каким углом к вертикали был наклонён стержень перед ударом?
(Всеросс., 2020, РЭ, 11)
Источники:
1) Найти скорость центра масс и угловую скорость стержня можно используя теорему Кёнига:
Для имеем:
Эта энергия представляет собой кинетическую энергию вращения системы относительно центра масс, – скорость
центра масс после удара. Поскольку поверхность гладкая, сразу после удара скорость центра масс направлена вертикально
вверх и определяется выражением
С учётом перпендикулярности и
Из закона сохранения энергии Подставляя это в выражение для
, получаем
Подставляя выражения для и
уравнение для
получим ответ для угловой скорости:
2) Ответ можно получить, используя тот факт, что для верхнего шарика выполняется закон сохранения импульса в проекции на ось, перпендикулярную стержню. Этот факт следует из того, что единственная сила, действие которой на верхний шарик за бесконечно малое время соударения существенно – это сила реакции стержня, направленная строго вдоль стержня. До удара проекция скорости шарика на эту ось равна
После удара, воспользовавшись законом сложения скоростей, получим для проекции
Из этих двух уравнений, используя ранее полученные выше выражения для и
, получаем ответ для
:
(Официальное решение ВсОШ)
| Критерии оценивания выполнения задачи | Баллы |
| Использовано при решении выражение для кинетической энергии гантели после удара в виде
| 2 |
| Из закона сохранения энергии получено
| 2 |
| Из определения скорости центра масс и закона сохранения энергии, с учётом перпендикулярности | 2 |
| Использовано для решения выражение для энергии вращения в системе центра масс | 2 |
| Получено верное выражение для угловой скорости | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




