Олимпиада им. Эйлера
Ошибка.
Попробуйте повторить позже
Будем говорить, что мы укоротили число, если стерли его последнюю цифру. Натуральное число, большее миллиона, таково, что если укоротить его, получится квадрат натурального числа, если укоротить этот квадрат, получится куб натурального числа, укоротив этот куб, получим четвёртую степень натурального числа, а, укоротив эту четвёртую степень, получим пятую степень натурального числа. Докажите, что если укоротить эту пятую степень, то получится шестая степень натурального числа.
Источники:
Пусть число после первого укорачивания равно а после третьего —
Тогда
отличается от
только двумя последними
цифрами, то есть
Так как по условию изначальное число больше миллиона, то
что возможно только если
(иначе
). Значит, вторая и третья
цифры исходного числа — нули, и куб
получающийся после второго укорачивания, оканчивается на
Следовательно,
четвертая и пятая цифры исходного числа — тоже нули (куб числа, делящегося на
делится и на
), и после пятого
укорачивания мы получим число
Поскольку в разложение числа, являющегося одновременно точным
квадратом и точным кубом, все простые множители входят в степенях, кратных
это число является точной шестой
степенью.
Ошибка.
Попробуйте повторить позже
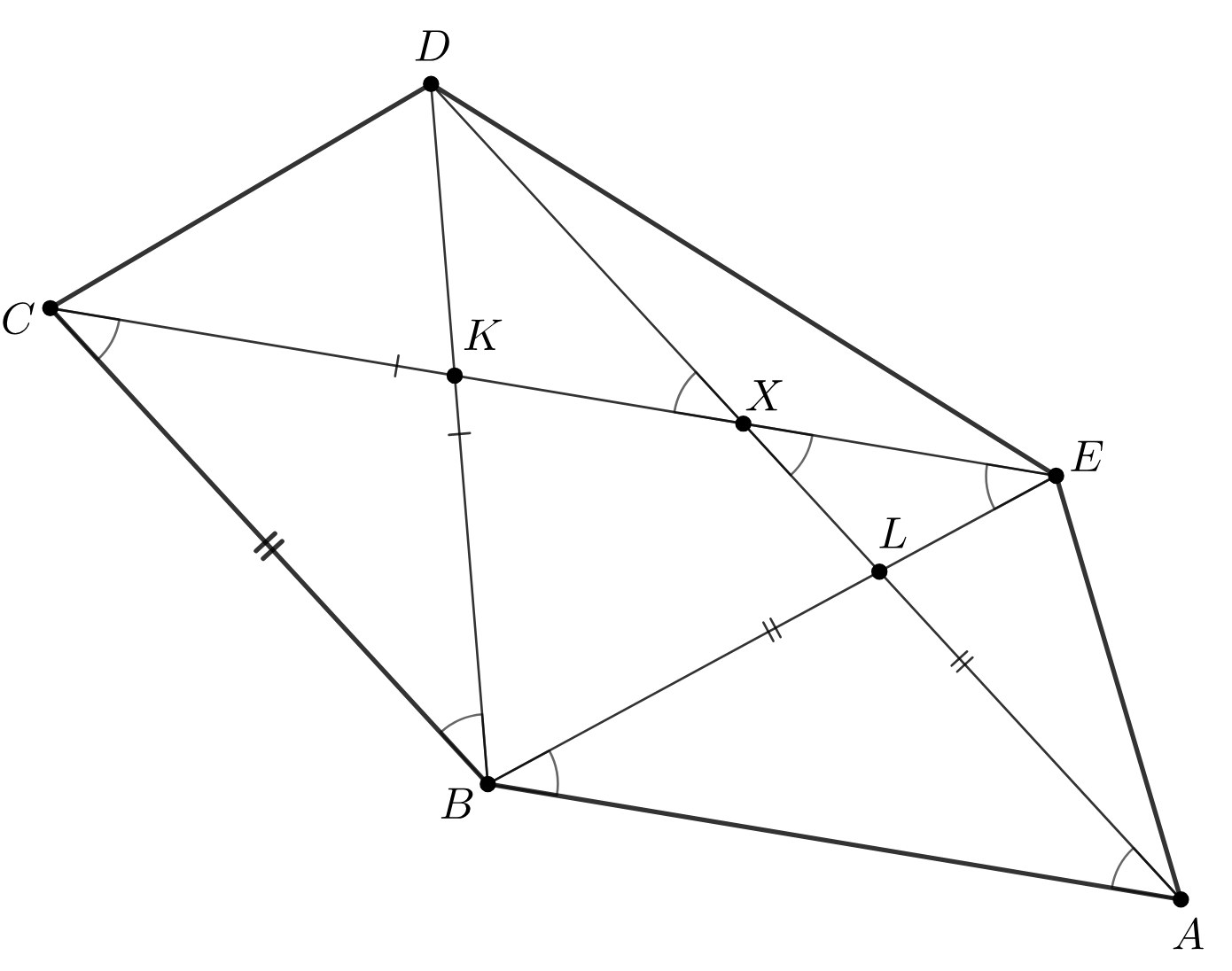
В выпуклом пятиугольнике диагонали
и
пересекаются в точке
Оказалось, что
— параллелограмм и
Докажите, что
Источники:
Т.к. — параллелограмм, то
и
Из получившихся равнобедренных треугольников
и
и параллелограмма
делаем вывод, что
Пусть
— пересечение
и
а
—
и
Тогда
По признаку
что и доказывает утверждение задачи.
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
равностороннего треугольника
Точки
и
на отрезках
и
соответственно
выбраны так, что
=
Найдите сумму углов
и
Источники:
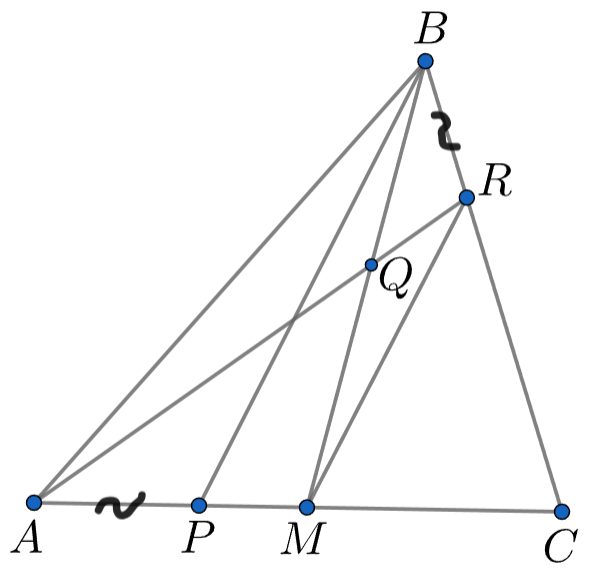
Пусть отрезки и
пересекаются в точке
. Так как треугольники
и
равны по первому признаку,
Тогда
(здесь первое равенство — теорема о внешнем угле для треугольника а второе — теорема о сумме углов для треугольника
), откуда
Ошибка.
Попробуйте повторить позже
Дано натуральное число большее
Докажите, что если число
— простое, то число
представляется в виде суммы
двух простых чисел.
Источники:
Как известно, Так как оба сомножителя в правой части тут меньше, чем
если
один из них — составное число, то у него есть делитель
больший
но не больший
Но тогда и число
делится на
что противоречит его простоте. Значит, числа
и
— простые, а в сумме они как раз дают
Ошибка.
Попробуйте повторить позже
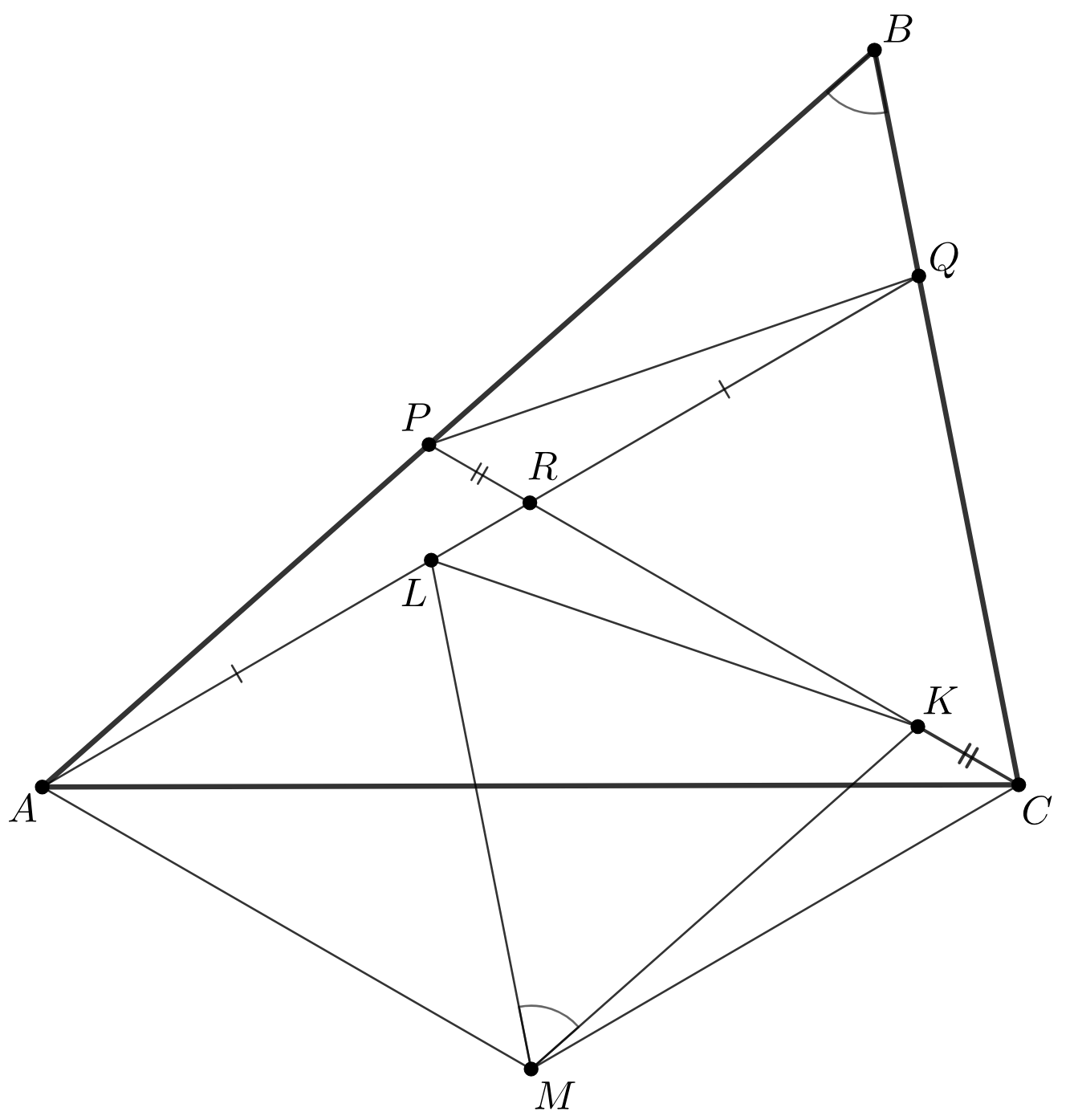
На сторонах и
треугольника
выбраны точки
и
соответственно. Отрезки
и
пересекаются в точке
Оказалось, что
Докажите, что из отрезков
и
можно составить треугольник, один из углов которого
равен углу
Источники:
Подсказка 1
Совсем непонятно, как получить то, что требуют в условии. Пожалуй, единственный понятный способ, это непосредственно получить этот треугольник с нужным углом на чертеже.
Подсказка 2
У нас есть странное условие AR = CR = PQ + QR. Как его применить, непонятно. Чтобы стало понятнее, нужны некоторые дополнительные построения, которые визуально отразят это условие.
Подсказка 3
Если разделить отрезки AR и RC точками на отрезки PR и RQ, то сразу становится проще с пониманием условия. Подумайте, как выгоднее это сделать.
Отметим точки и
на отрезках
и
соответственно таким образом, чтобы
а
Рассмотрим точку
симметричную
относительно середины отрезка
Нетрудно показать, что четырёхугольники
и
—
параллелограммы, поэтому треугольник
— искомый. В самом деле,
(так как прямые
и
ограничивают параллелограмм),
и, аналогично,
откуда
и
Ошибка.
Попробуйте повторить позже
Можно ли отметить в ряду натуральных чисел бесконечно много чисел так, чтобы разность любых отмеченных чисел (где из большего вычитается меньшее) была квадратом натурального числа?
Источники:
Пусть так отметить числа можно. Пронумеруем отмеченные числа в порядке возрастания: Положим
По условию в последовательности
любое число является квадратом натурального числа.
Кроме того, квадратом является любая сумма
Пусть
Очевидно,
Поэтому найдется такое
что
Сумма
тоже должна быть
квадратом некоторого натурального числа
При этом
откуда
Противоречие.
Нельзя
Ошибка.
Попробуйте повторить позже
Сумма дробных частей нескольких положительных чисел равна целой части их произведения. Докажите, что дробная часть суммы этих
чисел равна произведению их целых частей. Напомним, что целая часть числа
— это наибольшее целое число, не превосходящее
(например
), а дробная часть
числа
задается формулой
Источники:
Если дробная часть числа равна целому числу, то это Значит, надо доказать, что сумма наших чисел — целое число и произведение их
целых частей равно
Первое очевидно, так как по условию сумма дробных частей наших чисел — целое число. Допустим, второе неверно.
Тогда у всех наших чисел
целые части не меньше
и мы имеем
откуда что невозможно.
Ошибка.
Попробуйте повторить позже
Точки и
— середины сторон
и
соответственно треугольника
На продолжении отрезка
за точку
отмечена
точка
Оказалось, что
и
Докажите, что
Источники:
Обозначим через точку пересечения медиан
и
![]()
По свойству медиан и
Поскольку к тому же
то
Таким образом в треугольнике
медиана к стороне
равна
поэтому
Это означает, что
— высота треугольника
в котором
Следовательно,
— его медиана. Поэтому
откуда
Получается, что диагонали четырехугольника делятся точкой пересечения пополам, то есть — параллелограмм. Значит,
откуда
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырёхугольник На диагонали
выбрана точка
так, что
Точка
симметрична точке
относительно середины диагонали
а точка
симметрична точке
относительно прямой
Оказалось, что
и
Докажите, что
Источники:
Отметим на отрезке такую точку
что
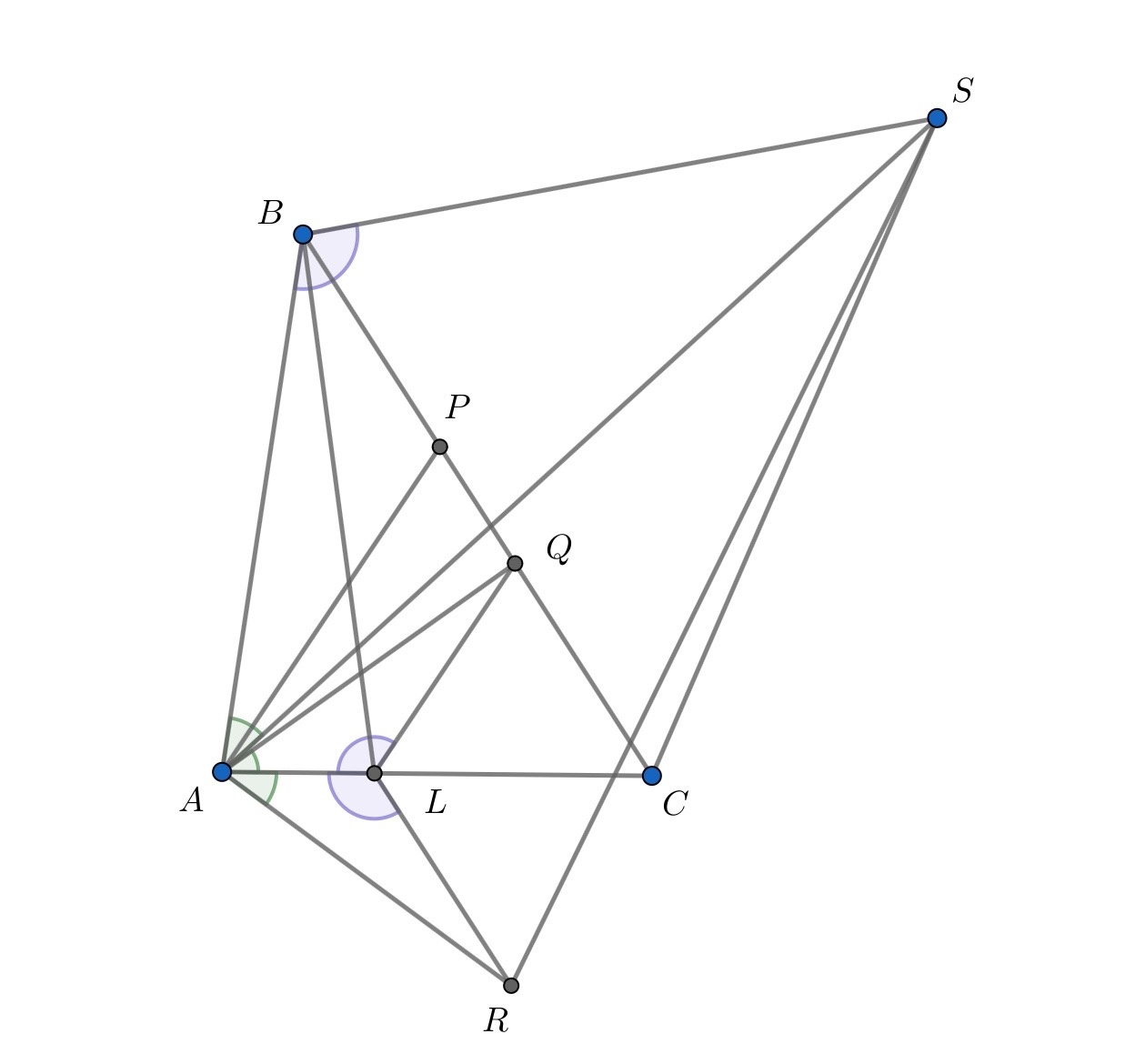
Тогда треугольники и
подобны и
Кроме того,
и
поэтому
треугольники
и
равны по двум сторонам и углу между ними. Следовательно,
Далее,
=
=
=
=
=
и
поэтому треугольники
и
подобны по двум углам, откуда
=
Значит, треугольники
и
подобны по двум
пропорциональным сторонам и углу между ними (
, поскольку
), но так как
то
Ошибка.
Попробуйте повторить позже
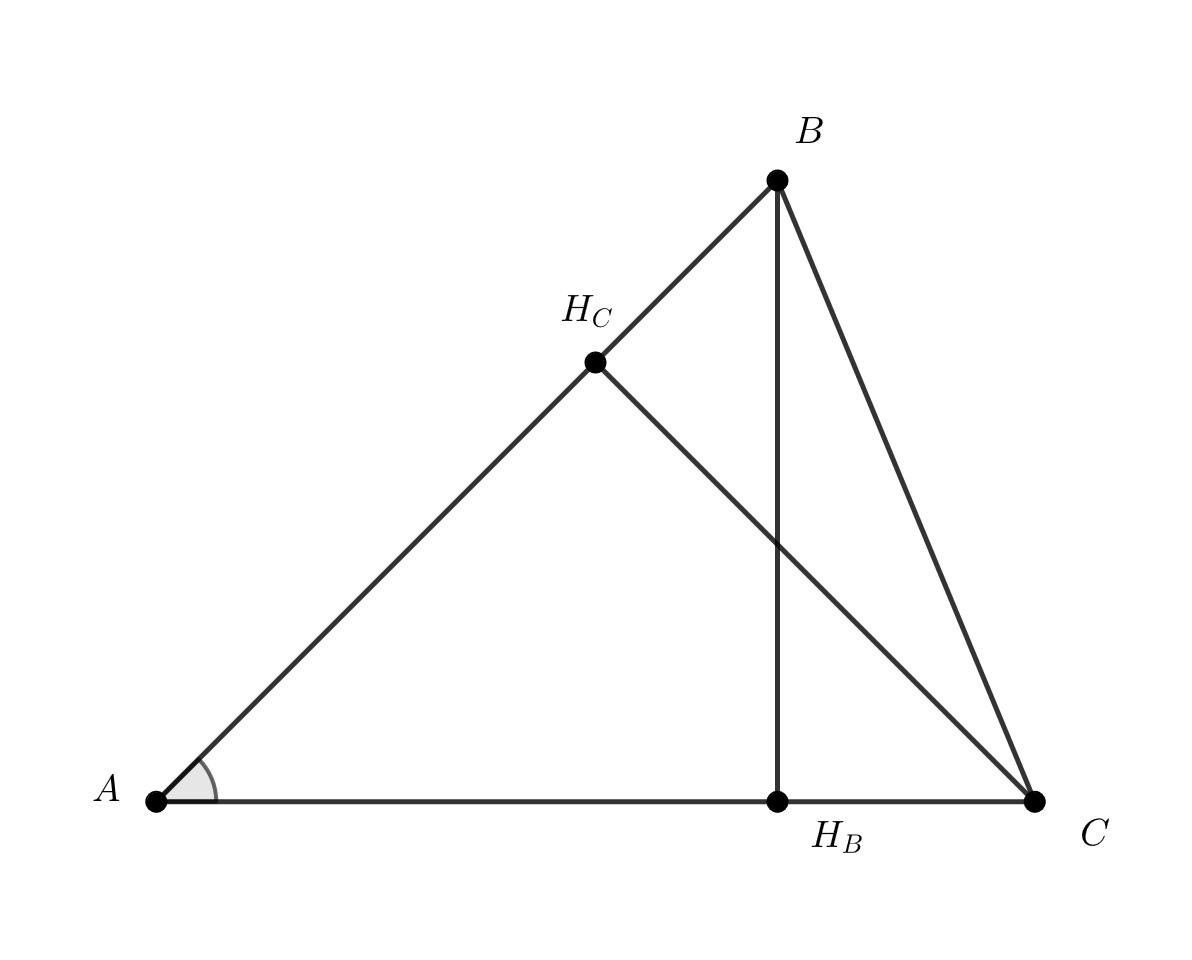
В остроугольном треугольнике угол при вершине
равен
градусам. Докажите, что периметр этого треугольника меньше
удвоенной суммы его высот, опущенных из вершин
и
Источники:
Заметим, что треугольники и
равнобедренные, а значит нам достаточно доказать, что
Теперь
заметим, что
Следовательно, треугольники
и
равнобедренные. То
есть неравенство превратится в
Это неравенство треугольника, а значит оно является верным, что и
требовалось.
Ошибка.
Попробуйте повторить позже
Внутри трапеции
где
взята точка
для которой
Точка
— середина отрезка
Докажите, что
Источники:
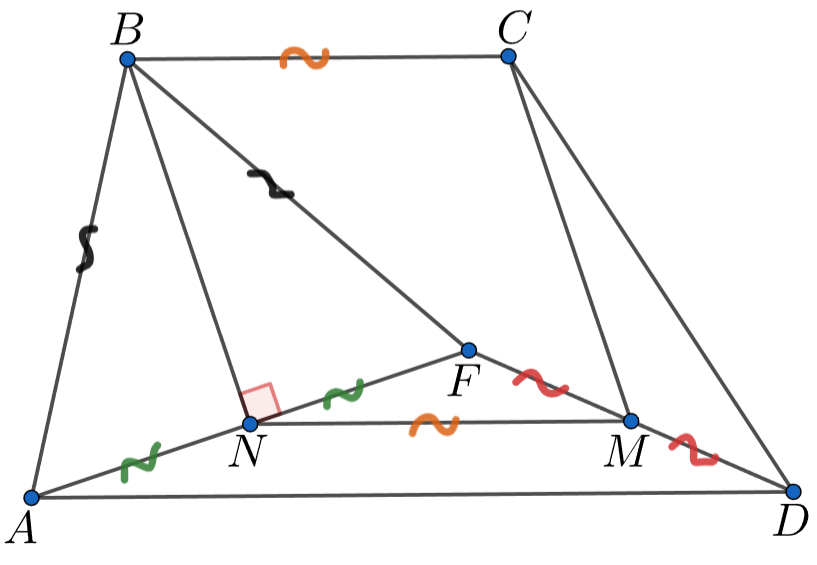
Пусть — середина отрезка
Заметим, что
а значит
параллельна и
Также
как средняя
линия треугольника
Таким образом, четырёхугольник
— параллелограмм. Следовательно,
Осталось заметить,
что
так как это медиана в равнобедренном треугольнике, проведённая к основанию.
Ошибка.
Попробуйте повторить позже
Можно ли из чисел вычеркнуть одно так, чтобы произведение оставшихся оказалось кубом натурального
числа?
Источники:
Подсказка 1
Понятно, что задача упирается в простые числа. Можно ли найти простое число, которое входит в небольшое количество имеющихся факториалов?
Подсказка 2
Верно! Число 97 входит только в 4 факториала. Тогда, чтобы создать куб, один из них нужно вычеркнуть. А можно ли посмотреть теперь на какое-то другое простое число?
Если произведение оставшихся факториалов — куб натурального числа, то для любого простого числа степень, в которой оно входит в это
произведение, должна делиться на Простое число
входит ровно в четыре факториала: от
до
и в каждый — в первой
степени. Поэтому вычеркнут должен быть один из этих четырех факториалов. Но тогда простое число
будет входить ровно в
факториалов: от
до
исключая вычеркнутый. Противоречие.
нельзя
Ошибка.
Попробуйте повторить позже
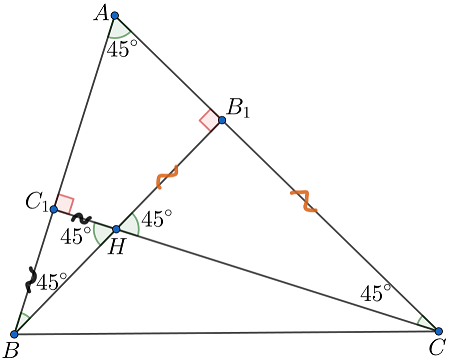
В остроугольном треугольнике угол при вершине
равен
Докажите, что периметр этого треугольника меньше удвоенной
суммы его высот, опущенных из вершин
и
Подсказка
В этой задаче нужно просто собрать информацию про рисунок. У вас есть угол 45 градусов и много прямых углов, образованных высотами. Поищите другие углы по 45 градусов, а потом воспользуйтесь для какого-то треугольника неравенством треугольника.
Пусть и
— основания высот из
и
соответственно, а
— ортоцентр треугольника
Тогда
поскольку Тогда треугольники
— равнобедренные. Значит,
и по неравенству треугольника. Просуммировав всё это, получим:
ЧТД.
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника равны и пересекаются в точке
Внутри треугольников
и
выбрали точки
и
соответственно так, что
Докажите, что прямая
параллельна биссектрисе угла
Источники:
Так как Так как
Пусть
и
— перпендикуляры, опущенные из
и
на
и
соответственно.
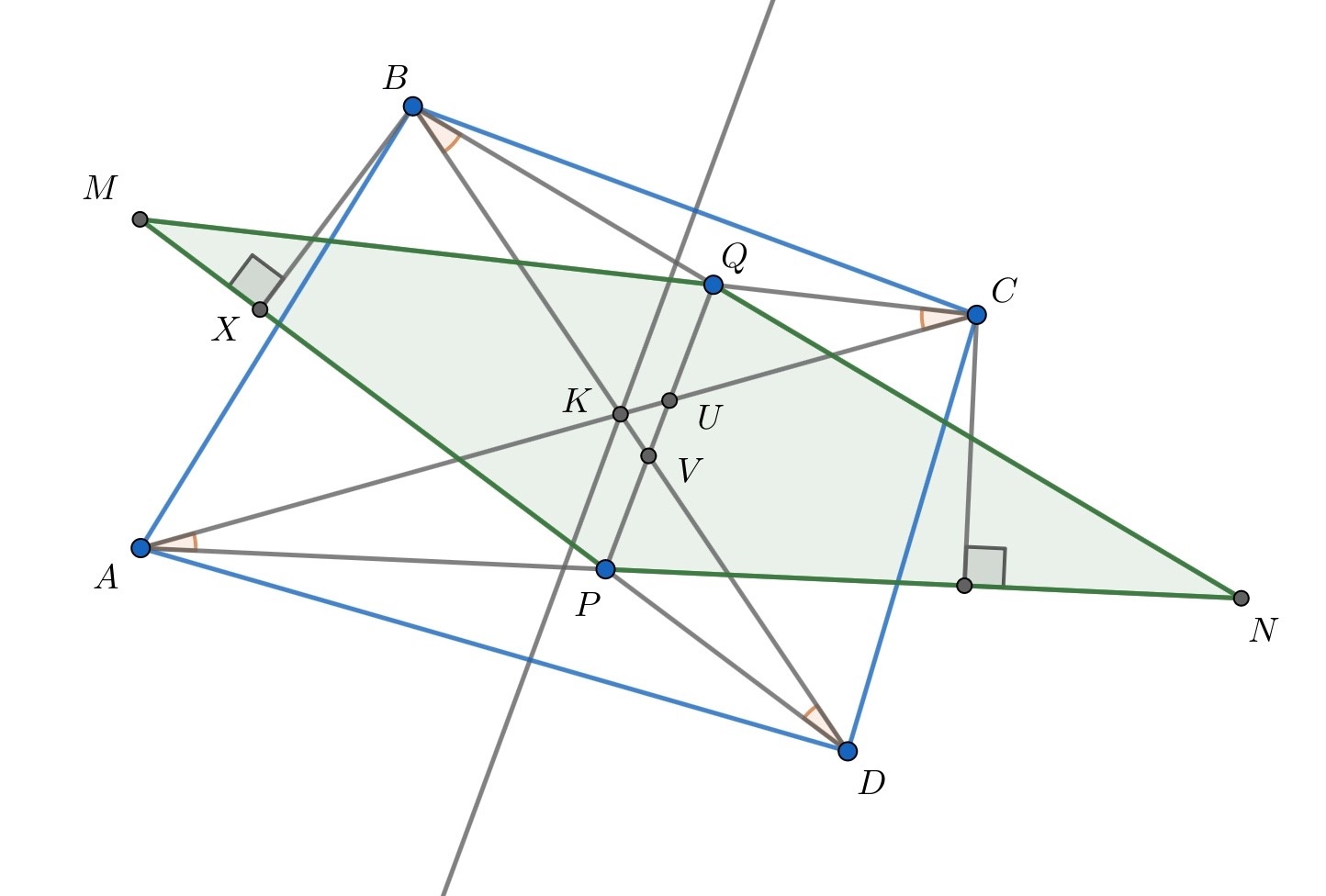
Тогда прямоугольные треугольники и
равны по гипотенузе и острому углу, откуда
Это значит, что
расстояния между прямыми
и
и между прямыми
и
равны. Таким образом, прямые
и
пересекаясь, образуют ромб
где
— точка пересечения
и
По свойству ромба
=
Пусть отрезок пересекает диагонали
и
в точках
и
соответственно. Тогда
=
=
Значит, в треугольнике
углы при основании
равны, он равнобедренный, и поэтому внешняя
биссектриса его угла
параллельна
что и требовалось. Если же
полученное равенство углов сразу говорит, что
—
биссектриса угла
Ошибка.
Попробуйте повторить позже
Внутри треугольника расположена точка
На стороне
выбрана точка
не совпадающая с серединой стороны. Оказалось,
что биссектриса угла
перпендикулярна стороне
угол
равен углу
и
Докажите, что
Источники:
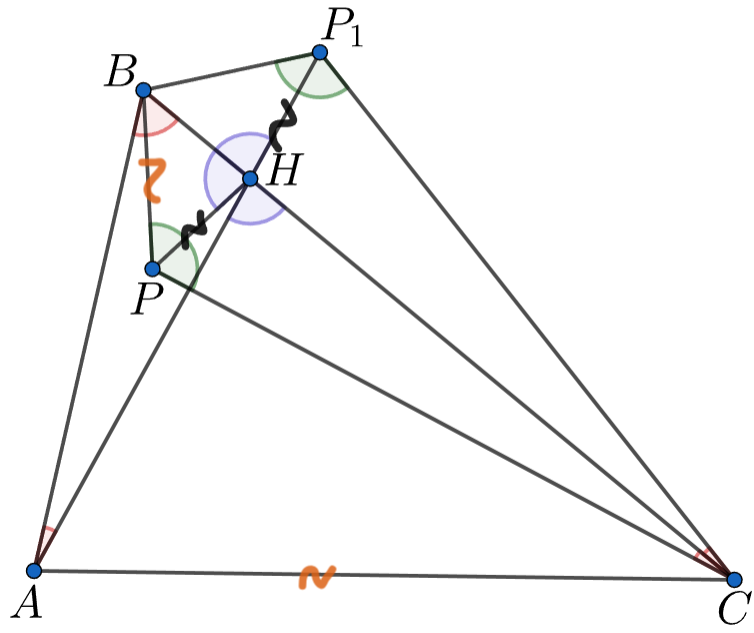
Запишем теорему синусов для треугольников и
Поскольку
и
получаем, что
Отсюда возникают два случая, либо углы
и
равны, либо они в сумме
дают
В первом случае четырёхугольник
был бы вписанным, но это невозможно, потому что по условию точка
лежит
внутри треугольника
. Следовательно, углы в сумме дают
Вспомним про то, что биссектриса угла перпендикулярна
На самом деле, это условие равносильно равенству
углов
и
Продлим
за точку
на длину отрезка
Получим точку
Углы
и
вертикальные, а значит
— биссектриса угла
Получается, что мы отразили точку
относительно
В таком
случае,
Также
то есть четырёхугольник
вписанный, потому что сумма
противолежащих углов равна
Но тогда
Таким образом, треугольник
равнобедренный, это даёт
требуемое.
Ошибка.
Попробуйте повторить позже
Найдите наименьшее натуральное такое, что для некоторого натурального числа
большего
и некоторого натурального числа
выполнено равенство
Источники:
Подсказка 1
Обозначим за c сумму a и k, за d нод a и c, тогда есть представления a=da₁ и c=dc₁. Приведём дроби к общему знаменателю, чтобы выразить сумму. Что получаем?
Подсказка 2
Получаем 1/b равна дроби с числителем a₁+c₁ и знаменателем da₁c₁. Отсюда можно сделать вывод о делимости d на a₁+c₁,тогда d² больше либо равно a+c. Какую оценку на d можно получить?
Подсказка 3
Верно, поскольку a+c больше 10⁶, d больше либо равно 1001, соответственно и k больше либо равно 1001. Получили оценку, осталось построить пример.
Оценка. Положим и НОД
Тогда
и
Так как числа
и
взаимно просты,
должно делиться на
Поэтому
и
откуда
и
Пример.
Ошибка.
Попробуйте повторить позже
Из клетчатой доски размером вырезали
клеток. Докажите, что доска распалась не более чем на
кусков. Два куска, не
имеющие общих точек кроме вершин клеток, считаются не соединёнными друг с другом.
Источники:
Нетрудно построить цикл, проходящий по разу через все клетки доски так, что соседние клетки в нем имеют общую сторону:
можно, например, пройти всю первую вертикаль от нижней клетки до верхней, потом ходить по вертикалям “змейкой” от верхней
горизонтали до второй снизу и обратно, а по последней вертикали вернуться на первую горизонталь и по ней — в исходную клетку.
“Расклеим” все общие стороны клеток на доске, кроме общих сторон между соседними клетками нашего цикла. Даже после этого
выброшенных клеток будут разбивать этот цикл не более чем на
частей, а при обратной склейке цикла в доску число частей не
увеличится.
Ошибка.
Попробуйте повторить позже
Вершина параллелограмма
лежит на стороне
параллелограмма
Известно, что
и
Докажите, что
Источники:
Подсказка 1
Как можно воспользоваться условием AE=2CD?
Подсказка 2
Давайте отметим точку M - середину отрезка AE (так мы получим, что AM = CD). Что можно сказать про четырехугольник ADCM?
Подсказка 3
Он является равнобокой трапецией. Выведите из этого равенство углов FEM и MDC. Что теперь достаточно доказать про углы MDE и MEB, что завершить доказательство?
Подсказка 4
Достаточно показать их равенство. Как это можно сделать?
Подсказка 5
Можно доказать, что треугольник MDE и BME подобны. Как это можно сделать?
Подсказка 6
Из равенства AC=CD следует равенство углов ACD и CDA. Воспользуйтесь этим, чтобы показать, что углы BMA и AMD равны. Тем самым, мы покажем равенство углов BME и EMD. Осталось проверить равенство отношений соответствующих сторон
Первое решение. Пусть — середина отрезка
Поскольку четырехугольник
— параллелограмм, точка
является
серединой отрезка
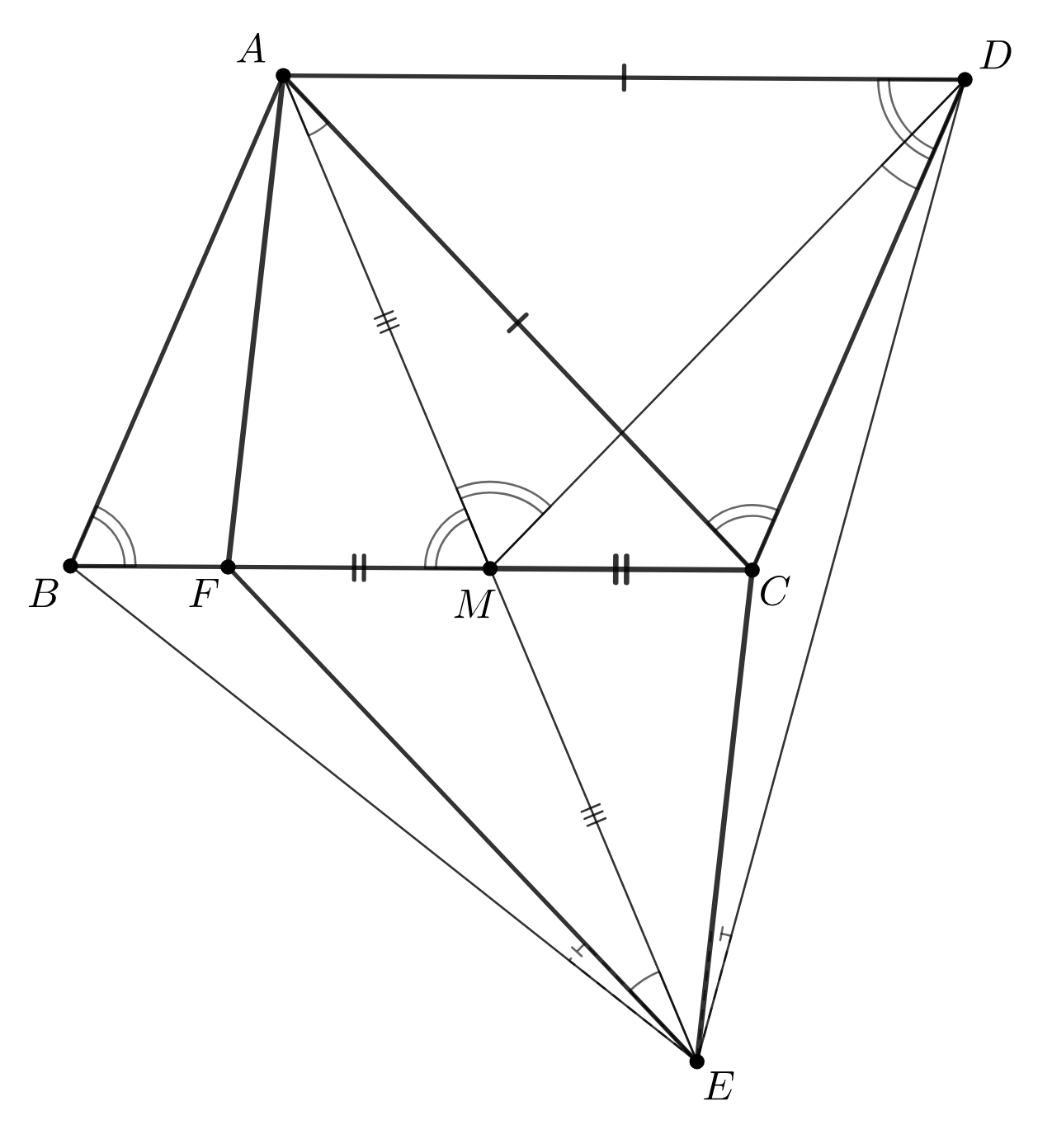
Обозначим и
Так как
— равнобокая трапеция,
откуда мы получаем что
и
Кроме того, поскольку
и
равнобедренные треугольники
и
подобны, поэтому
Треугольники и
также подобны, так как
и Значит,
откуда
что и требовалось.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Как и в первом решении, введём точку и покажем, что
— равнобокая трапеция. Отложим на луче
отрезок
Поскольку
перпендикуляры, опущенные на
из точек
и
равны,
откуда
Поэтому четырёхугольники
и
— также равнобокие трапеции; в частности,
вписана в некоторую окружность
С другой стороны, поскольку отрезки
и
параллельны и равны,
— параллелограмм, откуда
Значит,
— также равнобокая трапеция. Поскольку точки
и
лежат на
точка
лежит на этой же окружности. Из вписанного четырёхугольника
теперь получаем
Осталось заметить, что
— параллелограмм (ибо
параллелен и равен
), откуда
Ошибка.
Попробуйте повторить позже
Целые числа ,
,
и натуральное число
таковы, что
и
Докажите, что делится на
.
Источники:
Заметим, что в выражении нет переменной
Попробуем от неё избавиться и в исходных условиях. Для этого из
выразим
Теперь подставим полученное во второе условие:
Раскрываем скобки и получаем:
Приводим подобные слагаемые и после делим уравнение на 2:
Вернёмся к выражению В нём группируем кубы и квадраты, пользуемся формулами сокращенного
умножения:
Вынесем из обеих скобок:
Выше мы уже нашли, что вторая скобка равна тогда получаем
— целое число, поэтому
делится на
Ошибка.
Попробуйте повторить позже
Боря нарисовал девять отрезков, три из которых равны трём высотам треугольника три — трём биссектрисам, три — трём медианам.
Оказалось, что для любого из нарисованных отрезков среди остальных восьми найдётся равный ему. Докажите, что треугольник
—
равнобедренный.
Источники:
Пусть — самая короткая из высот треугольника
Если она равняется медиане
или биссектрисе
то
треугольник, очевидно, равнобедренный. Если она равна медиане
или биссектрисе
то тогда
не короче высоты
Значит, она равна
так как по нашему предположению
— самая короткая из высот. Итак, всё свелось к
случаю, когда
Но тогда прямоугольные треугольники
и
равны по катету и гипотенузе, откуда



