Трапеция
Ошибка.
Попробуйте повторить позже
Дана трапеция Известно, что
а биссектрисы углов
и
пересекаются в точке
лежащей внутри
трапеции. Докажите, что описанные окружности треугольников
и
касаются.
Источники:
Подсказка 1:
В данном случае для доказательства касания достаточно показать, что окружности имеют общую точку, лежащую на их линии центров. Подумайте, почему это так.
Подсказка 2:
Значит, нужно понять, какая прямая является их линией центров. Для этого нужно узнать какую-то дополнительную информацию про окружности. Обратите внимание на треугольник CED.
Подсказка 3:
Биссектрисы односторонних углов пересекаются под прямым углом, поэтому треугольник CED прямоугольный. А что можно сказать про прямую, содержащую его медиану, проведённую к гипотенузе?
Подсказка 4:
Чтобы она стала линией центров этих окружностей, она должна стать средней линией трапеции. Действительно, она же тогда будет проходить через середины боковых сторон.
По условию и
, поэтому
— основания трапеции. Пусть
и
— середины
и
так что
—
средняя линия трапеции
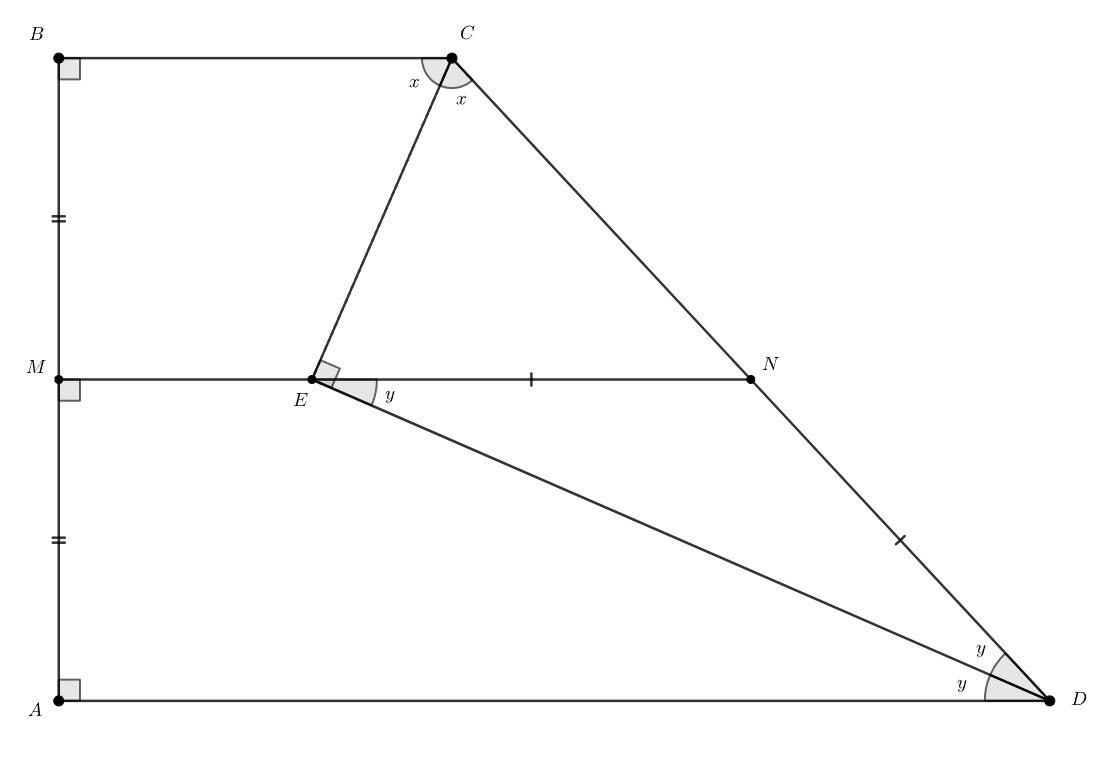
При этом параллельна основаниям, поэтому
и значит,
— серединный перпендикуляр к
Значит, центр
окружности
лежит на прямой
Положим
Из параллельности следует, что
, поэтому
.
Видим, что треугольник — прямоугольный (
), а значит,
— центр окружности
Далее, в прямоугольном треугольнике имеем
поэтому
, а из равенства углов
следует
поэтому
лежит на прямой
Итак, — общая точка окружностей
и
лежащая на их линии центров
Значит, эти окружности касаются (в
точке
).
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




