Регион 10 класс
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника 
перпендикулярны и пересекаются в точке 
Центры вписанных окружностей
треугольников 
являются вершинами выпуклого четырёхугольника, периметр которого равен
Докажите, что сумма радиусов вписанных окружностей треугольников 
не превосходит
Источники:
В прямоугольном треугольнике 
радиус вписанной окружности равен
(что также равно расстоянию от вершины прямого угла до точки касания катета со вписанной окружностью). Складывая это равенство с
аналогичными для треугольников 
получаем, что сумма 
радиусов вписанных окружностей треугольников 
равна
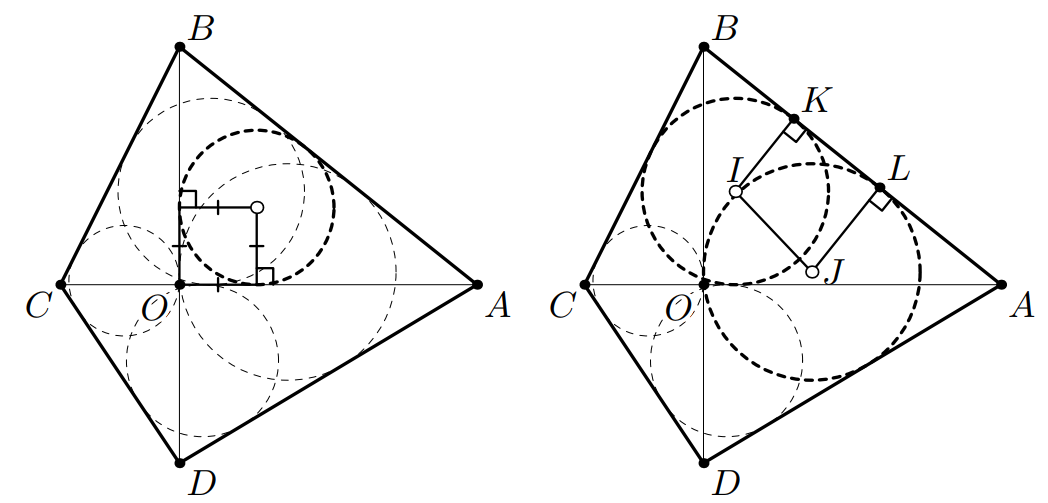
Пусть вписанные окружности треугольников 
и 
имеют центры 
и касаются стороны 
в точках 
и 
соответственно. Поскольку 
— проекция 
на прямую 
имеем
Сложим это неравенство с аналогичными для расстояний между другими парами центров вписанных окружностей треугольников 
Получим оценку на периметр 
:
Сравнивая с выражением для 
получаем требуемое неравенство 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
