Регион 10 класс
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Квадратный трёхчлен имеет два различных вещественных корня
и
Известно, что
Чему
может равняться
Источники:
Подсказка 1:
При виде суммы корней вы сразу должны подумать о теореме Виета. Её же некоторым образом можно выразить через коэффициенты трёхчлена.
Подсказка 2:
Как насчёт того, чтобы подставить это выражение в трёхчлен, вдруг получится что-нибудь интересное?
Первое решение. По теореме Виета Значит,
Тогда из условия следует, что
______________________________________________________________________________________________________________________________________________________
Второе решение. График симметричен относительно прямой
— вертикальной прямой, проходящей через
вершину параболы. Поэтому для любых двух значений
таких, что
будет выполнено
В
частности,
Но
______________________________________________________________________________________________________________________________________________________
Третье решение. Подставим в квадратный трехчлен:
Так как и
—– корни, то
а по теореме Виета
получаем, что
2025.
Ошибка.
Попробуйте повторить позже
В стране 30 городов и 30 двусторонних авиалиний, соединяющих города по циклу. Можно ли добавить дополнительно ещё 10 авиалиний так, чтобы после этого из любого города можно было добраться до любого другого не более чем за 4 перелёта?
Источники:
Подсказка 1:
Эта задача - конструктив. Попробуйте придумать пример.
Подсказка 2:
Для удобства введите нумерацию городов по кругу от 0 до 29. Попробуйте строить пример, опираясь на остаток при делении на 3 номеров городов. Это удобно, потому что, например, из любого города мы можем за не более чем 1 перелёт попасть в город с номером, кратным трём.
Подсказка 3:
А что, если соединить 0 город с остальными городами, номера которых кратны 3? Почему это рабочий пример?
Занумеруем города числами 0, 1, 2, …, 29 так, чтобы изначально у нас был цикл Добавим 9 авиалиний
…,
(а 10-ю авиалинию добавим какую угодно).
Покажем, что условие выполняется. Возьмем любые два города и
От
можно не более чем за 1 перелёт добраться до города
с номером, кратным 3. Аналогично, от
можно не более чем за 1 перелёт добраться до города
с номером, кратным 3. А между
городами
и
либо есть путь не более, чем из двух перелётов, так как все города с номерами, кратными 3, соединены с городом номер
0.
да, можно
Ошибка.
Попробуйте повторить позже
Положительные числа таковы, что
и
Докажите, что из чисел
какие-то два
отличаются более чем на 2.
Источники:
Подсказка 1:
Обратите внимание на слагаемые из левой части равенств? Они вам не встречались ни в каких известных разложениях?
Подсказка 2:
Рассмотрите выражение (a − b)(b − c)(c − a). Кажется, вы можете вычислить его значение.
Подсказка 3:
Пусть, не умаляя общности, c — наибольшее. Кажется, вы сможете упорядочить все три числа. Давайте заметим, что задача свелась к доказательству того, что c − a > 2.
Подсказка 4:
Давайте для удобства обозначим c − a = z, x = b − a, y = c − b. Используя равенство xyz = 2, нужно показать, что z > 2. А есть ли ещё какая-то связь между x, y и z?
Подсказка 5:
Давайте заметим, что x + y = z. Значит, можно оценить xy сверху, используя неравенство о средних. Не забывайте, что нас интересует строгая оценка z > 2.
Вычтем из второго равенства первое и разложим левую часть на множители, получим:
Не умаляя общности (в условии имеется циклическая симметрия переменных ), будем считать, что
—– наибольшее из данных
чисел. Тогда
но из (*) видим, что
Значит,
Аналогично
Тогда из (*) следует
Получается
Обозначим
так что
тогда (*) принимает вид
Нам нужно доказать,
что
Заметим, что так как это неравенство преобразуется к виду
(или следует из неравенства о среднем
арифметическом и среднем геометрическом). Отсюда
и далее
Получаем откуда
и поэтому
Остаётся показать, что невозможно. Если
то
и тогда в предыдущем рассуждении мы получим строгое
неравенство
Значит,
возможно лишь при
Рассмотрим этот случай отдельно.
В этом случае и
Тогда
что противоречит первому равенству из условия задачи.
Ошибка.
Попробуйте повторить позже
Можно ли на бесконечной клетчатой плоскости отметить конечное число узлов сетки так, чтобы было отмечено не менее двух точек, и для любой пары отмеченных точек нашлась бы отмеченная точка, равноудалённая от них?
Источники:
Подсказка 1:
Давайте раскрасим узлы в шахматном порядке и введём систему координат вдоль узлов сетки. Какие интересные наблюдения можно сделать?
Подсказка 2:
Могут ли быть отмечены узлы разных цветов?
Подсказка 3:
Пусть отмеченные точки A и B разных цветов, а C — равноудалена от них. Что можно сказать про чётность CA² и CB²?
Подсказка 4:
Итак, вы поняли, что все отмеченные узлы одного цвета. Предлагается следующая интересная идея. Что если через каждый узел этого цвета провести прямые с угловыми коэффициентами ±1 и рассмотреть новую сетку, образованную ими? Какие можно сделать наблюдения?
Подсказка 5:
Например, все отмеченные узлы принадлежат новой сетке. А если продолжить такие махинации, не возникнет ли противоречие?
Предположим, что требуемое возможно. Введём систему координат так, чтобы узлы являлись в точности точками с целыми координатами.
Раскрасим узлы сетки в шахматном порядке. Предположим, что нашлись два отмеченных узла разных цветов: — белый,
—
чёрный. Пусть нашёлся узел
, равноудалённый от них, и пусть, не умаляя общности,
— белый. Тогда у вектора
координаты
одной чётности, значит, по теореме Пифагора
равно сумме квадратов целых чисел одной чётности, т.е.
чётно. Аналогично
рассуждая, получаем, что
нечётно —– противоречие.
Итак, все отмеченные узлы имеют один цвет. Проведём через все узлы этого цвета прямые с угловым коэффициентом — получилась
новая квадратная сетка с шагом (длиной стороны квадрата)
Видим, что отмеченные точки являются узлами этой новой сетки.
Продолжая рассуждать аналогично, получим, что отмеченные узлы лежат на квадратной сетке с шагом
…. Но шаг сетки не может превышать константы — расстояния между двумя фиксированными отмеченными точками.
Противоречие.
Нельзя.
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного треугольника
пересекаются в точке
высоты треугольника
пересекаются в точке
точка
— середина стороны
Докажите, что
Источники:
Подсказка 1:
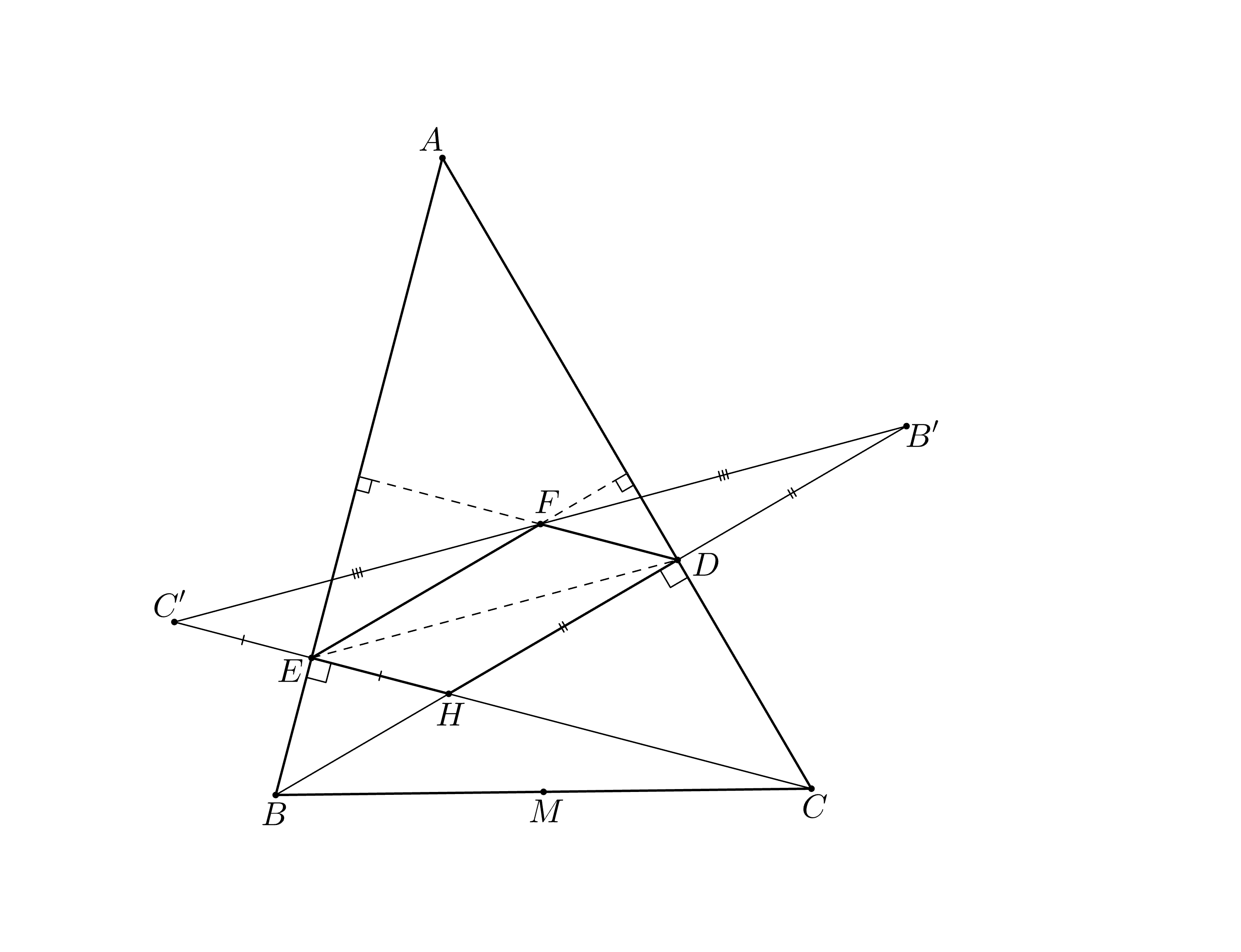
Хорошей идеей будет отражение точки H относительно BA и AC (назовём полученные точки C' и B'). Почему? Потому что BH = BC' и CH = CB' в силу симметрии. Есть ощущение, что новые отрезки проще связать с MF.
Подсказка 2:
Изучите получше чертёж. Поищите пары параллельных прямых. А что можно сказать про точки C', B' и F?
Подсказка 3:
F — середина C'B'. Теперь вернёмся к первой подсказке. Как связать MF с BC' и CB'? Учитывая, что нас просят доказать неравенство, можно попробовать выразить вектор MF через векторы BC' и CB', не забывайте, что M — середина BC.
Отразим относительно
получим точку
лежащую на
и такую, что
— середина
и
Аналогично,
точка
симметричная
относительно
такова, что
— середина
и
Так как имеем
Аналогично
Значит,
— параллелограмм. В треугольнике
точки
и
— середины сторон. Отметим также середину
стороны
тогда
— параллелограмм.
Получается, что
совпадает с
т.е.
— середина
Так как
и
— середины
и
имеем векторное
равенство
Тогда по неравенству треугольника () получаем
что равно
Этим доказано
нужное неравенство.
Ошибка.
Попробуйте повторить позже
Изначально на табло горит число 0. При нажатии на кнопку число на табло изменяется на 50 или 51. На кнопку нажали 2025 раз. Могло ли после этого на табло гореть число 25, если известно, что на табло не появлялись более чем двузначные числа, а также не появлялись отрицательные числа?
Источники:
Подсказка 1:
В этом процессе нужно найти полуинвариант.
Подсказка 2:
В контексте задачи будет выгодно разделить числа некоторым образом на две группы. Видимо, разделение будет таким, чтобы на каждом шагу было понятно, число из какой группы горит на табло.
Подсказка 3:
Давайте в первую группу возьмём числа от 1 до 49, а во вторую от 50 до 99. Число из какой группы будет после 2025 нажатий?
Первое решение. Назовём числа 0, 1, …, 49 маленькими, а остальные числа, которые могут появиться на табло, т.е. числа 50, 51, …, 99 — большими. Заметим, что после нажатия из маленького числа обязательно получается большое, а из большого числа — маленькое. Значит, после нечётного количества операций на табло будет гореть большое число.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Выстроим все целые числа от 0 до 99 в цепочку
Заметим, что если какое-то число горит на табло, то следующим числом может быть только соседнее число в цепочке. Но так как числа 0 и 25 стоят в цепочке на местах одной чётности, получить из числа 0 число 25 за нечётное количество шагов невозможно.
не могло
Ошибка.
Попробуйте повторить позже
Дана трапеция Известно, что
а биссектрисы углов
и
пересекаются в точке
лежащей внутри
трапеции. Докажите, что описанные окружности треугольников
и
касаются.
Источники:
Подсказка 1:
В данном случае для доказательства касания достаточно показать, что окружности имеют общую точку, лежащую на их линии центров. Подумайте, почему это так.
Подсказка 2:
Значит, нужно понять, какая прямая является их линией центров. Для этого нужно узнать какую-то дополнительную информацию про окружности. Обратите внимание на треугольник CED.
Подсказка 3:
Биссектрисы односторонних углов пересекаются под прямым углом, поэтому треугольник CED прямоугольный. А что можно сказать про прямую, содержащую его медиану, проведённую к гипотенузе?
Подсказка 4:
Чтобы она стала линией центров этих окружностей, она должна стать средней линией трапеции. Действительно, она же тогда будет проходить через середины боковых сторон.
По условию и
, поэтому
— основания трапеции. Пусть
и
— середины
и
так что
—
средняя линия трапеции
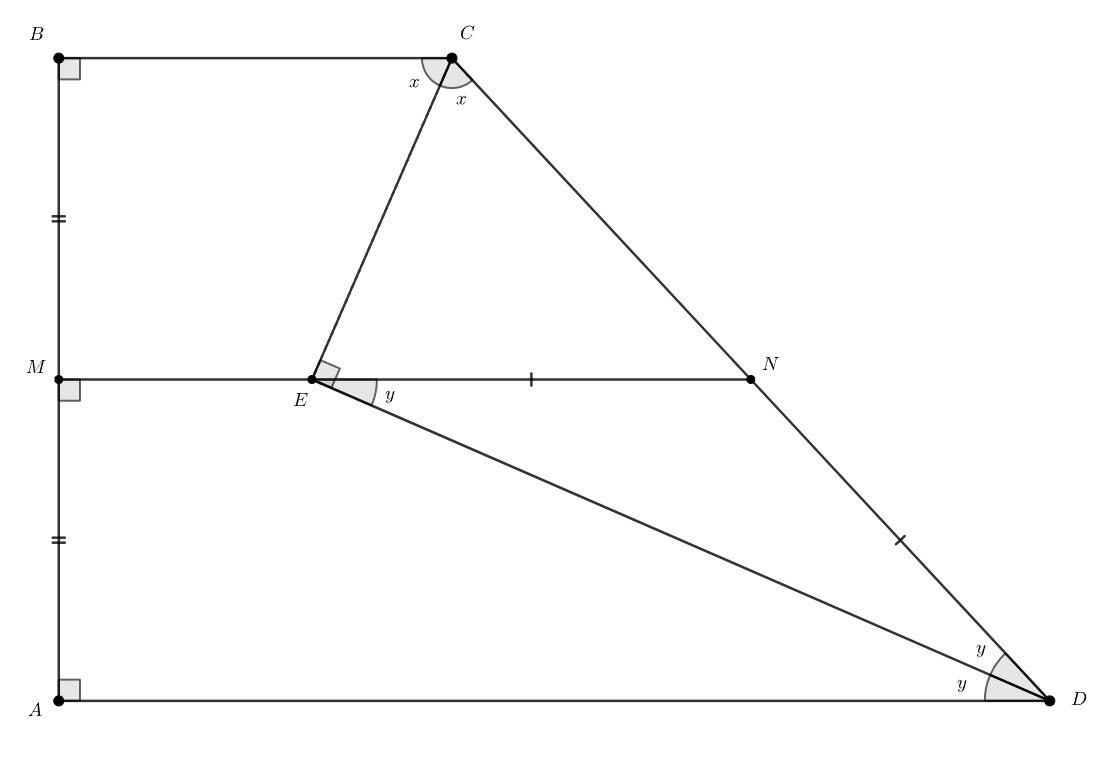
При этом параллельна основаниям, поэтому
и значит,
— серединный перпендикуляр к
Значит, центр
окружности
лежит на прямой
Положим
Из параллельности следует, что
, поэтому
.
Видим, что треугольник — прямоугольный (
), а значит,
— центр окружности
Далее, в прямоугольном треугольнике имеем
поэтому
, а из равенства углов
следует
поэтому
лежит на прямой
Итак, — общая точка окружностей
и
лежащая на их линии центров
Значит, эти окружности касаются (в
точке
).
Ошибка.
Попробуйте повторить позже
В клетчатом прямоугольнике каждую клетку красят в белый или чёрный цвет. Доминошкой будем называть клетчатый
прямоугольник
или
Оказалось, что существует единственный способ разбить данный прямоугольник
на доминошки
так, чтобы каждая доминошка покрывала хотя бы 1 чёрную клетку. Какое наибольшее количество клеток могло быть покрашено в чёрный
цвет?
Источники:
Подсказка 1:
Для оценки введём следующие термины: блок — две соседние горизонтальные доминошки, тёмная доминошка — доминошка с 2 черными клетками, светлая — с одной. Что можно сказать про блок в контексте условия задачи?
Подсказка 2:
В блоке не более двух черных клеток, иначе этот блок можно по-разному замостить двумя доминошками. Пусть имеется k тёмных доминошкек. Остальные 200 - 2k приходятся на блоки и светлые доминошки. Как можно оценить количество черных клеток среди них?
Подсказка 3:
Не более половины, потому что в каждой светлой доминошке и блоке не более половины клеток черные. Значит, всего черных клеток не больше 2k + (100 - k) = 100 + k. Таким образом, все свелось к оцениванию количества темных доминошкек.
Подсказка 4:
Чтобы его оценить, давайте поймём, с какими фигурами они могут граничить. Может ли вертикальная доминошка граничить с тёмной?
Подсказка 5:
Нет, ведь тогда их можно заменить на блок. Значит, тёмная доминошка может граничить только с блоком. Может ли к одному блоку примыкать несколько таких доминошкек подряд?
Подсказка 6:
Нет, ведь тогда их можно заменить на две горизонтальные. Какое минимальное количество клеток по горизонтали может быть между двумя соседними тёмными доминошками? Может ли оно быть менее 4?
Подсказка 7:
Используя эту информацию, можно оценить снизу количество вертикалей некоторым выражением от k. Учитывая, что вертикалей 100, получится оценка на k.
Подсказка 8:
Итак, скорее всего, вы получили, что вертикалей хотя бы 5k - 4, откуда получается оценка на 20 тёмных доминошек. Осталось придумать пример. Для удобства попробуйте разбить доску на большое количество одинаковых маленьких объектов. Например, в контексте задачи удобно работать с прямоугольником 2×5.
Пусть прямоугольник разбит на доминошки. Двигаясь слева направо, понимаем, что горизонтальные доминошки объединяются в
блоки
Далее под блоком понимаем такой блок
из двух горизонтальных доминошек.
Назовём хорошим разбиение на доминошки, в котором в каждой доминошке хотя бы одна клетка чёрная. Назовём раскраску хорошей, если при ней существует ровно одно хорошее разбиение.
1) Приведём пример хорошей раскраски, в которой 120 чёрных клеток. Красим первый столбец белым, следующие 3 столбца — черным, пятый столбец — белым, и далее продолжаем с периодом 5.
Тогда разобьём наш прямоугольник на прямоугольники и в каждом из них пусть слева и справа находятся блоки, а посередине —
вертикальная доминошка. Видим, что получено хорошее разбиение.
Покажем, что оно единственно. Посмотрим на границу между 5-м и 6-м столбцами. Эта граница не может находиться внутри блока,
значит, эта граница обязательно должна присутствовать в разбиении и отрезать прямоугольник Далее продолжим аналогичные
рассуждения с отрезанием прямоугольников
Остаётся разобраться, как может быть устроено хорошее разбиение для прямоугольника
В первом столбце не может быть вертикальная доминошка, поэтому в 1-м и 2-м столбцах точно находится блок. Аналогично в 4-м и
5-м столбцах находится вертикальный блок. Тем самым хорошее разбиение однозначно восстановлено. Обоснование того, что наша
раскраска хорошая, завершено.
2) Оценка. Рассмотрим хорошее разбиение прямоугольника В каждом блоке не более двух чёрных клеток, иначе мы можем
заменить две горизонтальные доминошки этого блока на вертикальные, и разбиение останется хорошим.
В вертикальной доминошке может быть одна чёрная клетка или две чёрных клетки. В первом случае вертикальную доминошку назовём
светлой, а во втором — тёмной. Если у нас тёмных доминошек, то в них
чёрных клеток, а остальная площадь
разбита на
блоки и светлые доминошки, т.е. в ней не более половины площади занимают чёрные клетки. Итого чёрных клеток не
более
Остаётся понять, что тёмных доминошек не более 20. Вертикальная доминошка не может граничить с тёмной доминошкой, иначе эту
пару можно заменить на блок (из двух горизонтальных доминошек), и разбиение останется хорошим. Значит, граничить с тёмной
доминошкой может только блок. К одному и тому же блоку слева и справа не могут примыкать две тёмные доминошки, иначе в
образованном ими прямоугольнике можно заменить все доминошки на горизонтальные, и разбиение останется хорошим. Рассмотрим
две ближайшие друг к другу тёмные доминошки. Промежуток (по горизонтали) между ними не может составлять 0, 1, 2 или 3
клетки (в последнем случае два блока, соседних с этими тёмными доминошками, должны пересекаться, что невозможно).
Суммируя длины промежутков для
пар ближайших тёмных доминошек, получаем, что количество вертикалей не
менее
Но оно равно 100. Отсюда и
что невозможно при
Неравенство
установлено. Доказательство
оценки завершено.
120
Ошибка.
Попробуйте повторить позже
Назовём натуральное число однобоким, если оно больше 1, и все его простые делители заканчиваются на одну и ту же
цифру. (Например, числа и
— однобокие, а число
— нет). Существует ли возрастающая
арифметическая прогрессия с разностью, не превышающей 2025, состоящая из 150 натуральных чисел, каждое из которых —
однобокое?
Источники:
Подсказка 1
Предположим, у нас есть арифметическая прогрессия с разностью d и первым членом a. Рассмотрим модуль m такой, что НОД(d, m) = 1. Что можно сказать о наборе остатков от деления любых m последовательных членов прогрессии на m?
Подсказка 2
Пусть p и q — два разных простых числа, оканчивающихся на разные ненулевые цифры. Ясно, что число, делящееся на p·q, не может быть однобоким. Если p·q ≤ 150, что тогда можно сказать о делимости разности d на p или q?
Подсказка 3
Для каждой такой пары (p, q) с p·q ≤ 150 разность d обязана делиться хотя бы на одно из чисел p или q. Какие пары маленьких простых чисел с произведением ≤ 150 можно найти?
Подсказка 4
Рассмотрим простые числа: 2, 5, 7, 11, 13. Любые два из них образуют пару с разными окончаниями и p·q ≤ 150. Значит, d должно делиться на все эти числа, кроме, возможно, одного. Чему равно минимальное произведение четырёх наибольших из них?
Теперь добавим пару (3, 19): 3·19 = 57 ≤ 150, окончания 3 и 9 разные. Как это влияет на оценку d? Сравните результат с 2025.
Пусть у нас есть возрастающая прогрессия с разностью из
однобоких чисел. Разберёмся, что мешает числу
быть слишком
маленьким.
_________________________________________________________________________________________________________________________________________________________________________________
Утверждение. Пусть взаимно просто с натуральным
Тогда среди любых
последовательных членов арифметической
прогрессии с разностью
есть член, делящийся на
Более того, числа
дают все различных остатков при делении на
поскольку если остатки у чисел
и
для некоторых
совпали, то
должно делиться на
а значит, в силу взаимной простоты
и
должно
делиться на
что неверно.)
_________________________________________________________________________________________________________________________________________________________________________________
Далее, пусть и
— два простых числа, оканчивающиеся на разные цифры, причём такие, что
назовем такую пару
вредной. Тогда если
не делится ни на одно из чисел
то, согласно утверждению, в нашей прогрессии есть член, делящийся на
что невозможно для однобокого числа.
Вывод: для каждой вредной пары простых чисел делится хотя бы на одно из них.
Теперь рассмотрим простые числа
Любые два из них образуют вредную пару, значит,
делится на все эти
числа, кроме, возможно, одного. Кроме того,
и
— тоже вредная пара, значит,
делится хотя бы на одно из них.
Отсюда
противоречие.
не существует
Ошибка.
Попробуйте повторить позже
На графике функции отметили 1000 различных точек, абсциссы которых — целые числа из отрезка [0; 100000]. Докажите, что
можно выбрать шесть различных отмеченных точек
таких, что площади треугольников
и
равны.
Источники:
Подсказка 1
Зная координаты вершин треугольника, несложно подсчитать его площадь. Можно ли упростить формулу, зная, что вершины находятся на параболе y = x²?
Подсказка 2
Площадь треугольника с абсциссами a, b, c равна S = ½ · |(c − a)(c − b)(b − a)|. Заметьте, что площадь зависит только от разностей абсцисс точек.
Подсказка 3
При сдвиге абсцисс всех вершин на одно и то же число площадь сохраняется. Тогда стоит поискать отрезки одинаковой длины, чьи концы — подряд идущие отмеченные точки. Сколько равных отрезков гарантированно можно найти?
Подсказка 4
Пять отрезков – это минимум 6 различных точек. Может ли быть такое, что найдется не более четырех равных отрезков? Не окажется ли тогда суммарная длина отрезков с отмеченными концами больше 100000?
Вычислим площадь лежащего на параболе, через абсциссы его вершин. Без ограничения общности можем считать, что абсциссы
соответственно равны
Пусть
— проекции точек
на ось
Тогда площадь треугольника
выражается через площади трапеций:
По формуле площади трапеции:
Аналогично:
Подставляя и преобразуя, получаем:
Для точек на той же параболе с абсциссами
разности сохраняются:
Следовательно, тогда
Положим
Упорядочим абсциссы отмеченных точек по возрастанию:
Рассмотрим отрезков
Если среди них найдутся 5 отрезков равной длины, то утверждение
задачи верно.
Упорядочим эти 5 отрезков по возрастанию левых концов: Возьмём точки:
где — общая длина отрезков. Ранее доказано, что
Все точки различны, так как
Предположим теперь, что среди отрезков нет пяти равной длины. Тогда для каждой длины
имеется не более четырёх отрезков
длины
Тогда минимальная сумма длин всех отрезков не менее:
Но сумма длин всех отрезков равна Противоречие.
Следовательно, обязательно существуют пять отрезков равной длины, и по доказанному можно выбрать шесть точек с равными площадями треугольников.
Ошибка.
Попробуйте повторить позже
На доске нарисован выпуклый -угольник
Каждую его вершину надо окрасить в черный или в белый цвет. Назовем диагональ
разноцветной, если ее концы покрашены в разные цвета. Раскраску вершин назовем хорошей, если
-угольник можно разбить на
треугольники разноцветными диагоналями, не имеющими общих точек (кроме вершин). Найдите количество хороших
раскрасок.
Источники:
Подсказка 1.
Нам надо понять вид всех хороших раскрасок. Для этого бывает полезно разобраться в примерах для маленьких n или потыкаться в различных конфигурациях точек.
Докажем индукцией по что в хорошей раскраске нет четырёхугольника, в котором соседние вершины имеют противоположные цвета
(будем называть такой четырёхугольник гадким).
База для очевидна. Теперь докажем переход от
к
Пусть в хорошей раскраске на
вершинах есть гадкий
четырёхугольник
причём, не умаляя общности, вершины
и
— чёрные, а
и
— белые. Рассмотрим одну из
триангуляций, которая соответсвует данной раскраске.
Если вершина не соединена рёбрами с вершинам, кроме своих соседей, то её соседи соединены, а значит, среди них есть чёрная
вершина
Не умаляя общности, вершины идут так:
-
-
-
-
-
но тогда в многоугольнике без вершины
раскраска должна быть правильной, при этом есть гадкий четырёхугольник
По предположению индукции получаем
противоречие.
Если же вершина соединена ребром не со своим соседом — белой вершиной
(не умаляя общности, вершины идут так:
-
-
-
-
то в одном из многоугольников, на которые делит ребро
исходный многоугольник, есть гадкий
четырёхугольник
но раскраска при этом должна остаться правильной. По предположению индукции получаем
противоречие.
Теперь разобьём многоугольник на блоки подряд идущих вершин одинакового цвета. По вышедоказанному блоков не больше 2 (иначе найдётся гадкий четырёхугольник), но одного блока быть не может, так как оба цвета, очевидно, присутствуют. Тогда блоков всего 2 и таких раскрасок
(выбрать начало чёрного блока — способов, а после этого белого —
способ).
Заметим, что все такие раскраски подходят, а значит, всего существует хороших раскрасок.
Ошибка.
Попробуйте повторить позже
У Олега есть набор из 2024 различных клетчатых прямоугольников размеров
…,
(по одному прямоугольнику
каждого размера). Может ли он, выбрав некоторые из них, составить какой-нибудь клетчатый квадрат площадью больше
1?
Источники:
Подсказка 1:
Предположим, что это возможно. Пусть n — наибольшая из длин выбранных прямоугольников. Попробуйте как-нибудь оценить площадь квадрата.
Подсказка 2:
Например, ясно, что его площадь не меньше n², поскольку сторона не меньше n. Возможно, можно найти какое-то противоречие с этим?
Подсказка 3:
Какой может быть наибольшая площадь выбранных прямоугольников?
Предположим противное, и пусть — наибольшая из длин выбранных прямоугольников. Тогда составлен клетчатый квадрат
где
Значит, его площадь не менее
С другой стороны, его площадь не больше, чем суммарная площадь всех
прямоугольников
то есть не больше
Противоречие.
не сможет
Ошибка.
Попробуйте повторить позже
В ряд выписаны по одному разу все натуральные числа от 1 до 1000 в каком-то порядке. Докажите, что можно выбрать несколько стоящих подряд выписанных чисел, сумма которых больше 100000, но не превосходит 100500.
Источники:
Среди наших чисел где-то есть Покажем для начала, что можно выбрать числа с одной стороны от числа
так, чтобы их сумма
была больше 100000. Сумма всех без чисел без
равна
Тогда по принципу Дирихле с одной из сторон от числа сумма чисел не меньше 250000. Тогда, очевидно, с одной
стороны от числа
можно выбрать несколько подряд идущих чисел так, чтобы их сумма превосходила 100000. Без
ограничения общности будем полагать, что эти числа находятся справа от
(то есть числа, общая сумма которых не
меньше 250000). Обозначим эти числа
…,
где
— первое число справа от
— второе число и так
далее.
Выберем наименьшее такое что
Если теперь
то мы уже нашли подходящие числа. Предположим, что это не так. Тогда — наименьшее такое число, что
поскольку
в силу выбора Покажем, что сумма
подходит.
Во-первых, все слагаемые этой суммы в нашем ряду стоят подряд.
Во-вторых, по условию. Обозначим
Тогда и, следовательно,
Остается доказать, что эта сумма не превосходит Для этого используем знание о том, что
Тогда
Ошибка.
Попробуйте повторить позже
На координатной плоскости нарисована парабола Для данного числа
рассматриваются трапеции, вписанные в эту параболу
(то есть все вершины трапеции лежат на параболе), у которых основания параллельны оси абсцисс, а произведение длин равно
Докажите, что продолжения боковых сторон всех таких трапеций проходят через одну точку.
Источники:
Подсказка 1:
Попробуйте ввести координаты и написать уравнение боковой стороны AB. Если внимательно на него посмотреть, вы увидите эту точку.
Подсказка 2:
Пусть точки A и B имеют координаты (a, a²) и (b, b²). Тогда уравнение AB примет вид y = (a + b)x − ab. По всей видимости, мы хотим получить точку, у которой координаты будут выражаться через k.
Подсказка 3:
Обратите внимание на величину ab, она фиксирована и равна k²/4.
Пусть — одна из рассматриваемых трапеций,
и
Пусть точки
и
имеют координаты
и
Легко получить уравнение прямой
что после сокращения на превращается в
Но равно произведению половин оснований трапеции. Отсюда
Следовательно, прямая
проходит через фиксированную
точку
![]()
Ошибка.
Попробуйте повторить позже
По кругу стоят 100 белых точек. Аня и Боря красят по очереди по одной ещё не покрашенной точке в красный или синий цвет, начинает Аня. Аня хочет, чтобы в итоге оказалось как можно больше пар разноцветных соседних точек, а Боря — чтобы оказалось как можно меньше таких пар. Какое наибольшее число пар разноцветных соседних точек Аня может гарантировать себе независимо от игры Бори?
Источники:
Подсказка 1:
Попробуйте рассмотреть простую стратегию (она будет одинаковой для обоих игроков).
Подсказка 2:
Пусть Аня на каждом ходу ищет пару из неокрашенной и окрашенной точки, красит неокрашенную в противоположный цвет. Сколько пар она сможет создать?
Подсказка 3:
Учтите, что в конце игры количество разноцветных пар должно быть чётным. Почему это так?
Подсказка 4:
Стратегия Бори аналогична. Почему он не позволит Ане создать более 50 пар?
Нужно показать, что Аня всегда может добиться, чтобы разноцветных пар было не меньше 50, а Боря сможет помешать ей добиться, чтобы таких пар было больше 50.
Аня красит в любой цвет любую точку, а дальше каждым ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной (такая, очевидно, найдётся), и красит непокрашенную точку в цвет, отличный от цвета покрашенной. При этом образуется новая пара соседних разноцветных точек.
Боря каждым своим ходом выбирает пару из непокрашенной точки и стоящей рядом с ней покрашенной, и красит непокрашенную точку в цвет, совпадающий с цветом покрашенной. При этом образуется новая пара соседних одноцветных точек.
Всего в круге имеется 100 пар соседних точек, и каждый игрок делает по 50 ходов. В итоге Боря добьётся того, что хотя бы 50 пар будут одноцветными, а Аня — что хотя бы 49 пар будут разноцветными. Однако количество разноцветных пар всегда чётно. Действительно, после окончания игры пройдём полный круг, начиная с какой-либо отмеченной точки (пусть для определённости с красной). Группы из идущих подряд красных и синих точек будут чередоваться: К—С—К—С—…—К, и значит, встретим пар разноцветных соседей вида К—С столько же, сколько пар вида С—К. Поэтому если пар разноцветных соседних точек не меньше 49, то их хотя бы 50.
50
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника перпендикулярны и пересекаются в точке
Центры вписанных окружностей
треугольников
являются вершинами выпуклого четырёхугольника, периметр которого равен
Докажите, что сумма радиусов вписанных окружностей треугольников
не превосходит
Источники:
Подсказка 1.
В задаче надо сравнить два странных выражения. Давайте постепенно выражать их через более понятные отрезки. Начнём с суммы радиусов вписанных окружностей. Что можно заметить про треугольники, в которые вписаны наши окружности?
Подсказка 2.
Правильно! Они прямоугольные! Попробуйте вспомнить (или вывести), как выражается радиус вписанной окружности прямоугольного треугольника через его стороны.
Подсказка 3.
На самом деле радиус вписанной окружности треугольника AOB равен (OA + OB − AB)/2. Что получится, если сложить все четыре радиуса? Попробуйте выразить сумму только через отрезки, содержащие вершины четырёхугольника ABCD.
Подсказка 4.
Правильно! AC + BD - P/2, где P — периметр ABCD. Теперь хотелось бы получить похожее выражение для P. На самом деле отрезки между центрами вписанных окружностей посчитать хорошо, скорее всего, не получится, но можно оценить их длину снизу. Как это сделать?
Подсказка 5.
Стоит заметить, что у соседних вписанных окружностей есть общая касательная. Это может помочь в оценке?
Подсказка 6.
Да! На самом деле расстояние между центрами можно оценить через длину общей внешней касательной, которую уже несложно выразить через стороны исходного четырёхугольника ABCD. Попробуйте это сделать и сравнить с тем, что мы получили в сумме радиусов вписанных окружностей.
В прямоугольном треугольнике радиус вписанной окружности равен
(что также равно расстоянию от вершины прямого угла до точки касания катета со вписанной окружностью). Складывая это равенство с
аналогичными для треугольников
получаем, что сумма
радиусов вписанных окружностей треугольников
равна
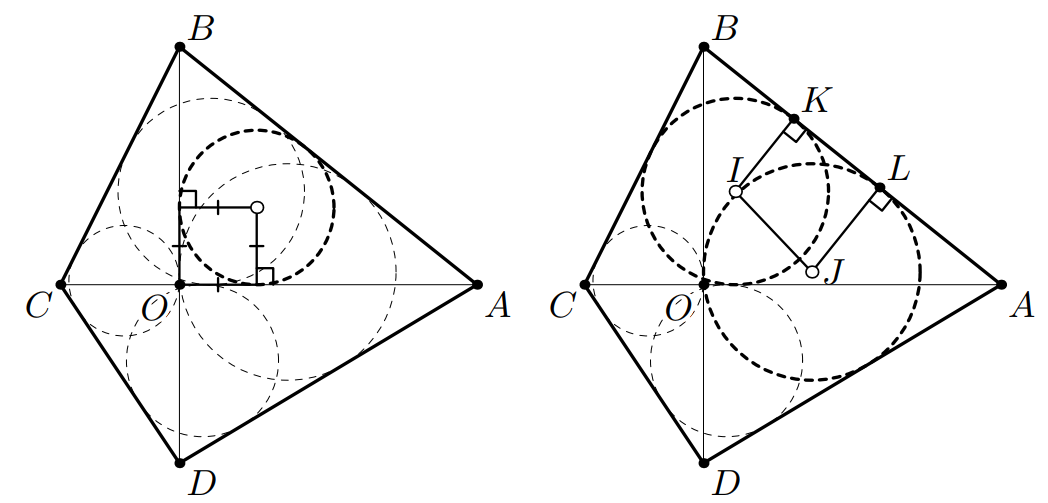
Пусть вписанные окружности треугольников и
имеют центры
и касаются стороны
в точках
и
соответственно. Поскольку
— проекция
на прямую
имеем
Сложим это неравенство с аналогичными для расстояний между другими парами центров вписанных окружностей треугольников
Получим оценку на периметр
:
Сравнивая с выражением для получаем требуемое неравенство
Ошибка.
Попробуйте повторить позже
Сергей утверждает, что нашел различные вещественные числа такие, что
Могут ли слова Сергея быть правдой?
Источники:
Подсказка 1:
Получается, что нужно либо придумать пример, либо доказать, что равенства не может быть. Если верен второй случай, то, скорее всего, выражение слева будет либо всегда меньше 4, либо больше. Главный вопрос — насколько выражение слева удобно для оценивания?
Подсказка 2:
Оно вполне себе удобное, ведь в знаменателе каждой дроби находится простой квадратный трёхчлен, значение которого можно оценить снизу, а саму дробь, следовательно, сверху.
Заметим, что
причем равенство достигается только при Тогда первое слагаемое
То же верно и для других слагаемых. Значит, левая часть уравнения Сергея не превышает причем равенство достигается
лишь при равенстве всех переменных
значит, равенство невозможно для различных
не могут
Ошибка.
Попробуйте повторить позже
Петя утверждает, что он написал 10 подряд идущих натуральных чисел, и оказалось, что среди всех цифр, используемых в этих числах, каждая цифра (от 0 до 9) встречается одно и то же количество раз. Могли ли слова Пети оказаться правдой?
Источники:
Подсказка 1:
Попробуйте придумать пример с такими числами.
Подсказка 2:
Ясно, что последние цифры этих чисел в некотором порядке представляют собой набор цифр от 0 до 9. Значит, достаточно поработать с цифрами чисел, кроме последней.
Подсказка 3:
Если каждое число без последней цифры будет содержать одинаковое количество всех цифр, это даст требуемое.
Примером могут служить числа вида
где в качестве
можно взять любое
число, состоящее из одинакового количества всех цифр от
до
например, любую перестановку цифр
где
не является
первой цифрой.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. На самом деле, можно показать, что все возможные примеры устроены так. Заметим, что каждая из цифр
появляется по разу в разряде единиц у рассматриваемых чисел. Предположим, что наименьшее из чисел на доске заканчивается не нулем,
то есть происходит переход через разряд между числами, оканчивающимися на
и
Рассмотрим последовательность из 10 подряд идущих натуральных чисел:
Предположим, что в этой последовательности происходит переход через степень (например, от
к
). Иными словами,
есть числа разной длины. Пусть числа от
до
имеют
цифр, а числа от
до
–
цифр, где
Тогда:
- Количество чисел с
цифрами:
- Количество чисел с
цифрами:
Так как всего 10 чисел:
Общее количество цифр:
По условию, общее число цифр делится на (каждая из 10 цифр встречается одинаковое количество раз), получаем
противоречие, ведь
не делится на
Следовательно, переход невозможен, и все 10 чисел имеют одинаковое количество цифр
Рассмотрим число то есть все разряды исходного без единиц, количества вхождений цифр в эти разряды также равны между
собой. Пусть оно имеет вид:
где – это первая с конца цифра не равная 9, тогда
Заметим, что в точно входит каждая цифра, отличная от
ведь иначе
и
имеют больше вхождений: в этом случае
у них есть вхождение в некоторые числа не в разряде единиц, а другие его не имеют, поскольку второй переход через разряд в
последовательности невозможен. Тогда для них общее количество вхождений в разряды за исключением единиц кратно
ведь
не
меняется при переходе через разряд. Тогда это верно и для всех цифр. Заметим, что среди
есть хотя бы одно число не равное
или
и количество его вхождений в разряды, кроме единиц, по модулю
равно количеству чисел либо до перехода через разряд, либо
после, то есть не равно
противоречие.
Цифра входит суммарно
раз, где
— количество вхождений в запись
то есть в записи
всех цифр поровну, тогда
последовательность имеет требуемый вид:
могли
Ошибка.
Попробуйте повторить позже
Дан четырёхугольник в котором
Известно, что его вершины
и
вместе с серединами сторон
и
лежат на одной окружности. Докажите, что вершины
и
вместе с серединами сторон
и
тоже лежат на одной
окружности.
Источники:
Первое решение. Обозначим через
середины сторон
соответственно. По условию, четырехугольник
— вписанный. Значит,
Поскольку — средняя линия треугольника
то
поэтому
Пусть отрезки
и
пересекаются
в точке
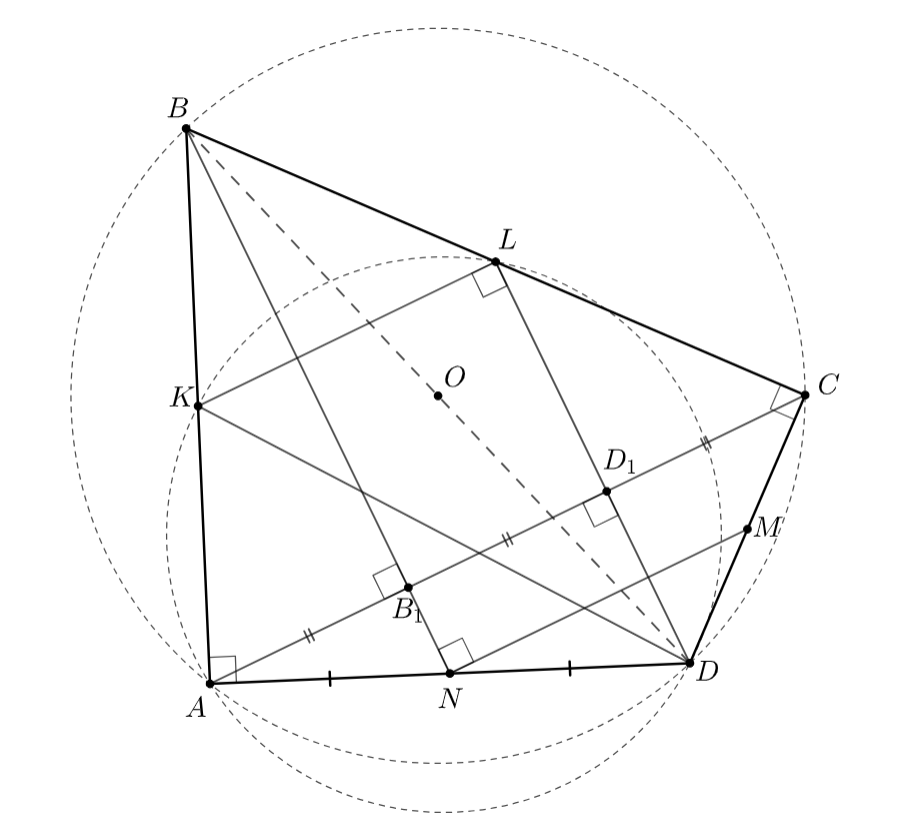
Опустим из точки перпендикуляр
на прямую
Тогда
значит,
— середина отрезка
по теореме
Фалеса. Кроме того, четырехугольник
вписан в окружность, построенную на отрезке
как на диаметре,
обозначим центр этой окружности через
Вновь по теореме Фалеса проекции точек
и
на прямую
находятся
на равном расстоянии от проекции точки
то есть от середины отрезка
Из этого следует, что
Итого,
Значит, — средняя линия в треугольнике
поэтому
Поскольку еще и — средняя линия треугольника
то
Следовательно, точки
и
лежат на окружности с диаметром
что и требовалось доказать.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Воспользуемся обозначениями из первого решения,
середины сторон
соответственно. Поскольку
— средняя линия треугольника
то
Отсюда и из вписанности четырехугольника
мы получаем равенства углов:
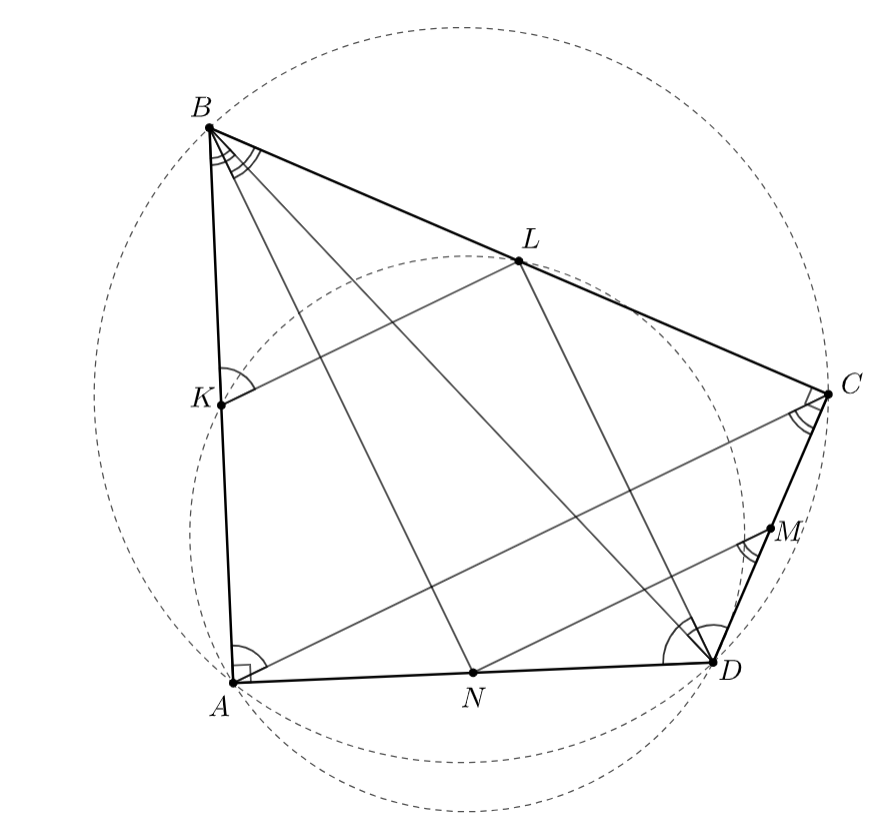
Таким образом, вписанность четырехугольника равносильна равенству углов
что эквивалентно равенству
Последнее равенство равносильно подобию треугольников и
что эквивалентно равенству отношений их
катетов
Домножая на знаменатели, получаем соотношение
Рассуждая аналогично, получаем, что это же равенство равносильно вписанности четырехугольника Поскольку
—
средняя линия треугольника
то
Отсюда и из вписанности четырехугольника
мы получаем равенства
углов:
Таким образом, вписанность четырехугольника равносильна равенству углов
что эквивалентно равенству
Последнее равенство равносильно подобию треугольников и
что эквивалентно равенству отношений их
катетов
Домножая на знаменатели, получаем соотношение
что завершает данное доказательство.
Ошибка.
Попробуйте повторить позже
Найдите все тройки (не обязательно различных) натуральных чисел такие, что каждое из чисел
является
простым делителем числа
Источники:
Подсказка 1:
Давайте сначала предположим, что все три числа различны. Может ли одна скобка делиться на два числа из этих трёх?
Подсказка 2:
Нет, ведь произведение любых двух чисел больше любой скобки. Докажите это. Значит, каждая скобка делится на какое-то из этих чисел. Давайте заметим, что условие задачи инвариантно относительно перестановки переменных. Поэтому давайте их упорядочим и рассмотрим наименьшую скобку. В каких случаях наименьшая скобка может делиться на какое-то из чисел?
Подсказка 3:
Пусть теперь какие-то из чисел совпали. В каком случае это возможно и как будет выглядеть условие?
Подсказка 4:
Итак, вы пришли к тому, что среди a, b, c точно есть единица. Пусть это c. Тогда 2(a² + 1)(b² + 1) должно делиться на простое число a + b. Обратите внимание на НОД скобочек.
Подсказка 5:
Итак, вы пришли к тому, что хотя бы два числа из a, b, c должны быть 1. Пусть это b и c. Тогда 4(a² + 1) должно делиться на a + 1. Посмотрите на НОД a² + 1 и a + 1.
Видим, что
удовлетворяет условию. Далее будет доказано, что других ответов нет.
1) Предположим, что
делится на где
это следует из условия, если дополнительно предполагать, что различны.
Заметим, что один из трех сомножителей
не может делиться на произведение двух из чисел
так как он меньше этого произведения. Действительно, рассмотрим, например,
Из раскрытия скобок видим,
что
и аналогично
Следовательно, каждый из сомножителей
должен делиться ровно на одно из чисел
Пусть, для
определенности,
— наименьшее из чисел
Тогда
и
поэтому
может делиться на
только в
случае
и
т.е в случае
Далее, и
поэтому
может делиться на
только в случае
и
т.е в
случае
Аналогично, может делиться на
только при
2) Пусть какие-то два из трех чисел совпадают, скажем,
Тогда
Значит, либо либо
Первый случай возможен лишь при
иначе
— составное число, что дает противоречие. Значит, в любом случае среди присутствует единица, скажем,
Тогда наши данные простые числа — это
и
и они должны быть делителями
Если хотя бы одно из чисел больше 1, то
и на
обязан делиться хотя бы один из сомножителей
и
А поскольку разность
делится на получаем, что оба числа
делятся на
Тогда если
отлично от
то
делится на
что разобрано в случае
Остается вариант
Рассуждаем как в предыдущем случае и получаем, что хотя бы два из трех чисел обязаны равняться
Пусть,
например,
Случай уже был ранее. Если
то
— нечетное простое, значит
должно делиться на
Отсюда
должно делиться на Но это невозможно, так как
и — простое.



