Регион 10 класс
Ошибка.
Попробуйте повторить позже
На сторонах выпуклого четырёхугольника 
во внешнюю сторону построены прямоугольники. Оказалось, что все вершины этих
прямоугольников, отличные от точек 
лежат на одной окружности. Докажите, что четырехугольник 
—
вписанный.
Источники:
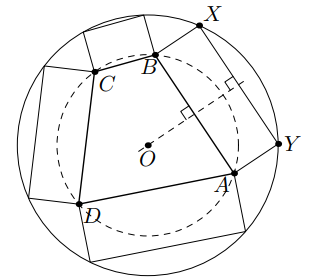
Пусть 
— один из данных прямоугольников, а 
— центр окружности, на которой лежат восемь вершин из условия задачи.
Тогда 
лежит на серединном перпендикуляре к отрезку 
Но он совпадает с серединным перпендикуляром к отрезку
Поскольку 
лежит на нём, имеем 
Аналогично доказываем, что 
и 
Тогда 
равноудалена от всех вершин четырехугольника 
значит, 
вписан в окружность с центром 
что и требовалось
доказать.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
