Закл (финал) 11 класс
Ошибка.
Попробуйте повторить позже
В пространстве даны три отрезка 
и 
, не лежащие в одной плоскости и пересекающиеся в одной точке 
. Обозначим
через 
центр сферы, проходящей через точки 
и 
. Докажите, что прямые 
и 
пересекаются в одной точке.
Источники:
Для любого отрезка 
серединным перпендикуляром к этому отрезку назовем плоскость, перпендикулярную ему и проходящую через
его середину, т. е. геометрическое место точек, равноудаленных от 
и 
Пусть 
— серединный перпендикуляр к отрезку 
Тогда 
(поскольку на каждой такой сфере лежат обе точки
Легко видеть, что 
поскольку обе перпендикулярны прямой 
Аналогично определим плоскости
для 
и 
для 
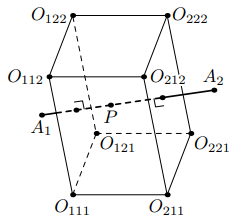
Поскольку шесть выбранных плоскостей попарно параллельны, то они образуют
параллелепипед, осталось заметить, что его вершинами будут точки 
Действительно, каждая точка лежит в 
плоскостях
(например), откуда и следует нужное. Учитывая, что диагонали параллелепипеда пересекаются в одной точке, всё
доказано.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
