Закл (финал) 11 класс
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дано натуральное число Натуральные числа
выписывают на доске в строчку в некотором порядке. У каждых двух стоящих
рядом чисел вычисляют их НОД (наибольший общий делитель) и записывают этот НОД на листке. Какое наибольшее количество
различных чисел может быть среди всех
выписанных на листке чисел?
Источники:
Подсказка 1:
Давайте начнем с оценки. Вот если есть два различных числа a, b и их НОД равен d, можно ли как-то оценить эти числа, используя d? И как, используя эти оценки, оценить сверху d некоторым выражением от n?
Подсказка 2:
Одна из самых очевидных оценок: min(a, b) ≥ d, max(a, b) ≥ 2d. Отсюда следует, что n ≥ 2d, откуда d ≤ [n / 2]. Осталось привести пример.
Подсказка 3:
Чтобы найти расстановку, для которой любое число d ≤ [n / 2] будет выписано, можно сделать так, чтобы числа вида d и 2d стояли рядом.
Подсказка 4:
Тут на помощь могут прийти числовые цепочки вида a, 2a, 2²a, ... Подумайте, почему они могут быть полезны, и как реализовать расстановку с ними?
Оценка. Предположим, что какое-то из выписанных на листке чисел больше скажем,
Тогда наибольшее из
чисел
не меньше
что больше
– противоречие (НОД двух чисел, не превосходящих
не превосходит
). Значит,
каждый из написанных
ов не превосходит
потому количество различных
ов не может превышать
Пример. Разобьём все числа от до
на цепочки вида
где
— нечётное число, не превосходящее
Выпишем
в строчку цепочки одну за другой. Тогда для любого натурального
найдётся цепочка, в которой встречается
а следующее за
число будет
Видим, что каждое натуральное
будет выписано на листке.
Ошибка.
Попробуйте повторить позже
На доску выписали 777 попарно различных комплексных чисел. Оказалось, что можно ровно 760 способами выбрать два числа и
записанных на доске, так, чтобы выполнялось равенство
Способы, которые отличаются перестановкой чисел, считаются одинаковыми. Докажите, что можно выбрать такие два числа и
записанных на доске, что
Источники:
Подсказка 1:
Для начала стоит переписать условие в более удобном виде. На что может намекать сумма квадратов и удвоенное произведение по разные стороны от знака равенства?
Подсказка 2:
Верно! На квадрат разности. Имеем (a − b)² = −1, то есть a − b = ±i. Аналогично преобразуем выражение, которое нужно доказать: (с − d)² = −45. Итого, нужно найти пару с разницей 45i. Что это означает?
Подсказка 3:
Нужно найти 46 "подряд идущих" чисел с разницей в i. Формально, мы хотим найти числа a₁, a₂, ..., a₄₆ с разницей ровно i между соседними. Тогда a₁ и a₄₆ будут являться искомой парой. В подобных задачах бывает полезно ввести граф.
Подсказка 4:
Разумеется, вершины — числа, ребро проводим, если разница между числами равна i. Хотим найти путь длины 46. Какие замечания можно сделать про этот граф?
Подсказка 5:
Осознайте, что в нём нет циклов, а также степень каждой вершины не более двух. Что же это означает?
Подсказка 6:
Граф представляет собой набор непересекающихся простых путей (так называемых бамбуков). Докажите это самостоятельно. Каждый такой путь — отдельная компонента связности, являющаяся деревом. Вершин в графе 777, рёбер — 760. Какой вывод из этих фактов можно сделать?
Подсказка 7:
В графе ровно 17 компонент связности (докажите это), то есть 17 путей, общая длина которых 760. Дело за малым — докажите, что путь длины хотя бы 45 найдется. Успехов!
Заметим, что условие равносильно тому, что
или же Рассмотрим граф, вершины которого — записанные на доску числа, а ребро проводится между двумя числами,
которые отличаются на
Согласно условию задачи, в таком графе ровно 760 рёбер. Каждая компонента связности этого
графа представляет собой путь и состоит из вершин-чисел вида
…,
Предположим, что в
этом графе
компонент связности. Тогда в нём
рёбер, поэтому
Поскольку
то в
какой-то компоненте связности хотя бы 46 вершин, поэтому какие-то две из этих вершин — это числа
и
Тогда
следовательно,
что и требовалось.
Ошибка.
Попробуйте повторить позже
Дана прямая призма Известно, что треугольники
и
— остроугольные. Докажите, что
точки пересечения высот этих треугольников вместе с точкой пересечения медиан треугольника
лежат на одной
сфере.
Источники:
Обозначим через и
точки пересечения медиан и высот треугольника
а также отметим точку
так,
что
Пусть сфера построена на отрезке
как на диаметре. Поскольку прямая
перпендикулярна плоскости
то точка
лежит на
Покажем, что на сфере
лежит точка пересечения высот
треугольника
рассуждение для двух других
треугольников аналогично.
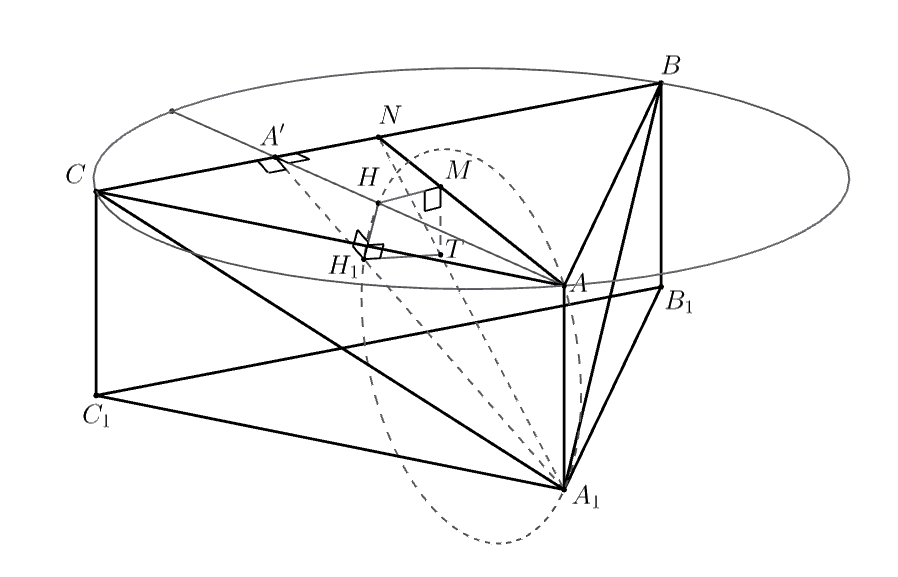
Обозначим через середину отрезка
Поскольку
точка
лежит на отрезке
в частности, она лежит в
плоскости
Пусть
— высота треугольника
Поскольку прямая
перпендикулярна плоскости
то
а также
по теореме о трёх перпендикулярах, то есть точка
лежит на отрезке
Поскольку точка, симметричная точке пересечения высот
треугольника
относительно прямой
лежит на его
описанной окружности, то
Применяя то же рассуждение для треугольника
мы получаем,
что
Следовательно, четырёхугольник вписанный, поэтому
Поскольку ещё
и
вновь применяя теорему о трёх перпендикулярах, мы получаем, что прямая
перпендикулярна плоскости
Значит,
то есть точка
лежит на сфере
что и требовалось.
Аналогично доказывается, что точки пересечения высот треугольников и
также лежат на сфере
Таким образом,
все пять точек (точки пересечения высот четырёх треугольников и точка пересечения медиан треугольника
) лежат на сфере
Ошибка.
Попробуйте повторить позже
Пару многочленов и
с целыми коэффициентами назовём важной, если из делимости на 100 обеих разностей
где — целые, следует, что числа
и
делятся на 100. Существует ли такая важная пара многочленов
и
что пара многочленов
и
тоже является важной?
Источники:
Подсказка 1:
Запишем в условие задачи в общем виде. У нас есть достаточное условие (А) для выполнения утверждения (В). Как вообще можно исследовать подобные конструкции? Например, подставить какой-то особенный набор в А, чтоб получить два утверждения В про него, которые либо наложат какие-то ограничения, либо приведут к противоречию. Разумеется, нас интересуют только остатки чисел по модулю 100, поэтому дальнейшие рассуждения ведутся в F₁₀₀. Подумайте, какие наборы было бы полезно подставить.
Подсказка 2:
Обратим внимание на то, что условие А зависит от функций, а утверждение В про их аргументы. Осознаем следующий факт: если аргументы одинаковые, то значения функций одинаковые, а вот наоборот работает не всегда. Благодаря этому мы можем провернуть один трюк. В условие А закинуть наборы функций, одинаковые по значению, но с разными аргументами. Тогда мы получим делимость на 100 для ненулевых разниц, а это уже продвижение. Заметьте, если бы было наоборот (условие А зависит от аргументов, а утверждение B про функции), то такой трюк бы не сработал. Теперь нужно понять, как именно осуществить предложенное.
Подсказка 3:
Начнём вводить обозначения в лоб. Пусть есть два набора (a ≥ b) и (c ≥ d) такие, что F(a, b) = F(c, d), G(a, b) = G(c, d). Тогда из условия А получаем, что a − c и b − d делятся на 100. Всё бы ничего, если a − c, b − d > 99. Такое вполне может быть. Но мы же хотим получить дополнительные ограничения...
Подсказка 4:
Значит, нужно ограничить a, b, c, d так, что a − c, b − d < 100. Какой самый простой способ это сделать?
Подсказка 5:
Просто взять a, b, c, d ≤ 99. То есть при этих ограничениях мы знаем, что если F(a, b) = F(c, d), G(a, b) = G(c, d), то (a, b) = (c, d). Отлично, давайте запишем теперь это построже и более масштабно.
Подсказка 6:
Рассмотрим всевозможные пары (a, b), где a, b ∈ F₁₀₀. Для каждой пары рассмотрим пару O(a, b) = [F(a, b), G(a, b)]. Мы поняли, что O(a, b) различны для различных пар (a, b). Но и пары (a, b) и пары O(a, b) — это просто комбинации остатков (mod 100). Что это значит?
Подсказка 7:
Что все пары O(a, b) — всевозможные пары остатков, причём каждая пара встречается один раз. Вернёмся к тому, о чём спрашивают в задаче. Если многочлены P(x, y) − xy и Q(x, y) + xy являются важной парой, то для них должно выполняться то же условие, что мы получили. Пока что не особо понятно, какой всё-таки ответ. В таких случаях нужно попробовать сначала доказать, что не существует, а если не получится это доказать (или хотя бы что-то нащупать), то уже пробовать строить пример. Итак, попробуем доказать, что не существует.
Подсказка 8:
Пусть для удобства теперь F(x, y) = P(x, y) − xy, G(x, y) = Q(x, y) + xy. O(x, y) = [F(x, y), G(x, y)], R(x, y) = [P(x, y), Q(x, y)]. Предположим, что F(x, y), G(x, y) — важные. Знаем, что набор {O(x, y), x, y ∈ F₁₀₀} = {R(x, y), x, y ∈ F₁₀₀} = {(x, y), x, y ∈ F₁₀₀}. Хотим найти противоречие. Доказывать, что какой-то пары остатков в {O(x, y)} нет — гиблый номер, ибо мы для этого ничего не знаем. Значит, нужно действовать хитрее и посмотреть на эти пары с другой точки зрения.
Подсказка 9:
Вся задача крутится вокруг модульной арифметики. Не будем же нарушать тенденции. Поскольку в {R(x, y)} есть всевозможные пары остатков, то там есть всевозможные пары с точки зрения чётности. Какой вывод из этого можно сделать?
Подсказка 10:
Осознайте, что если рассмотреть R(Ч, Н), R(Н, Ч), R(Ч, Ч), R(Н, Н) то мы получим перестановку набора (Н, Ч), (Ч, Н), (Н, Н), (Ч, Ч), где Ч, Н — произвольное чётное число и нечётное соответственно. Значит, для O(x, y) должно выполняться то же самое свойство. Но так ли это?
Подсказка 11:
Осталось просто разобрать случаи и осознать, что вот в этом и кроется проблема. У вас всё получится!
Пусть пара многочленов и
— важная. Рассмотрим пары остатков от деления на 100 чисел
и
где
—
всевозможные пары целых чисел от 0 до 99. Согласно условию задачи, все такие пары остатков разные. Поскольку всего пар чисел
то каждая пара остатков от деления на 100 достигается ровно один раз. Значит, достигаются все 4 возможные пары чётностей чисел
Поскольку чётность значения многочлена с целыми коэффициентами в точке
зависит только от чётности чисел
и
мы получаем, что пары значений
дают все четыре возможные пары чётностей. Однако заметим, что для пар многочленов и
первые три пары чётностей одинаковые, а последняя пара — разная. Следовательно, обе такие пары многочленов важными быть не могут.
не существует
Ошибка.
Попробуйте повторить позже
Дано натуральное число Куб со стороной
сложен из
единичных кубиков, каждый из которых — либо чёрный, либо
белый. Оказалось, что среди любых 8 кубиков, имеющих общую вершину и образующих куб
не более 4 чёрных кубиков. Какое
наибольшее количество чёрных кубиков могло быть использовано?
Источники:
Подсказка 1:
В подобных задачах всегда стоит поизучать примеры раскрасок, то есть не сразу делать оценку, а попробовать понять, как может выглядеть пример, заметить закономерности и так далее. Также частенько бывает очень полезно рассмотреть маленькие случаи, времени это много не займёт, а понимания может привнести достаточно. Итак, с чего начнём?
Подсказка 2:
Раз куб со стороной 2N + 1, то логичнее всего начать рассматривать случай куба 3×3×3. Исследуйте возможные примеры, удовлетворяющие условию.
Подсказка 3:
Уверены, пример на 18 вы построили, подумайте ещё и осознайте, что пример на 20 тоже строится несильно сложно. Теперь стоит подумать насчёт оценки...
Подсказка 4:
Она здесь тривиальная, рассмотрим два диагонально противоположных куба 3×3×3 и вот уже оценка на ≤ 20 готова (осознайте это). Итого, мы поняли, что для этого куба ответ 20. В такие моменты бывает очень полезно изучить число 20, а тем более то, как оно зависит от N (в нашем случае N = 1).
Подсказка 5:
20 = 2 * 2 * 5 = (N + 1)²(4N + 1) = 4N²(4N + 1) = 20N = 4N²(N+4) = ... (в случае N = 1). Также понятно, что ответ около трети от (2N+1)³. Очевидно, что в общем виде это многочлен с коэффициентом 4 при N³. Также естественное желание свести константы к минимуму (ну или оставить ± единички). На что это намекает?
Подсказка 6:
На то, что ответ, скорее всего, равен (N+1)²(4N + 1). Попробуем доказать эту гипотезу. С чего мы начнём?
Подсказка 7:
Разумеется, с примера, ведь подогнать пример под ответ проще, чем оценку (банально в силу наглядности). Итак, вперёд пробовать!
Подсказка 8:
Если вы достаточно попробовали, то, скорее всего, поняли, что совсем наглядно пример не строится (никакие красивые узоры не подходят), значит, нужно прибегать к аналитическому подходу...
Подсказка 9:
А от подобных мыслей недалеко до декартовой системы координат. Введём же её так, что все вершины единичных кубиков будут иметь целые координаты от 0 до 2N + 1. Рассмотрим произвольный куб 2×2×2. Хотим как-то в зависимости от координат вершин его кубиков определять его цвет.
Подсказка 10:
Но наборов координат всего 27, а кубиков 8, не хотелось бы рассматривать все эти наборы координат, в идеале для каждого кубика оставить свою координату, а ещё круче, если они будут выбраны "одинаково".
Подсказка 11:
Попробуем выбрать "наконечник" куба 2×2×2, то есть в каждом маленьком кубике рассмотрим вершину, которая ближе всего к началу координат. Этот наконечник образует куб из 8 вершин. Как координаты этих вершин записываются в общем виде?
Подсказка 12:
(a, b, c); (a + 1, b, c); (a, b + 1, c); (a, b, c + 1); (a + 1, b + 1, c); (a + 1, b, c + 1); (a, b + 1, c + 1); (a + 1, b + 1, c + 1). С какой точки зрения мы можем посмотреть на эти числа, учитывая, что a, b, c — произвольные?
Подсказка 13:
С точки зрения чётности! И нам нужно покрасить ровно 4 кубика в чёрный цвет. Как же это сделать?
Подсказка 14:
Давайте сделаем так, чтобы кубики, у которых в выбранном наборе координат хотя бы 2 чётные, будут чёрными, а остальные — белыми. Осознайте, что это искомый пример. Путём несложных вычислений докажите, что всего чёрных кубиков при такой раскраске ровно (N+1)²(4N+1). Осталось подогнать оценку под пример, однако наш пример уже достаточно сложный и идейный, может попробовать как-то использовать его в оценке?
Подсказка 15:
Давайте вместо отдельной оценки попробуем доказать оптимальность нашего примера (осознайте, что эти идеи разные). Пусть в общем виде кубик тёмный, если в нашем примере он чёрный, и светлый — если в примере он белый (то есть кубик вполне может быть тёмным и светлым одновременно). Раз пример аналитический, то оценка, скорее всего, такая же. В примере мы используем идеи чётности и расстояний, и они отлично работают, может стоит вновь прибегнуть к ним? Давайте для каждой целочисленной точки в нашей ДСК (a, b, c) введём определение t-ранга. t-ранг — минимальное расстояние до грани куба, перпендикулярной соответствующей оси (разумеется, t ∈ {x, y, z}). Значения рангов — r_x, r_y, r_z. А просто рангом точки (a, b, c) — r будем называть min(r_x, r_y, r_z). Вспомним про наши идеи, что можно сделать дальше?
Подсказка 16:
Отметим все целочисленные точки с нечётным рангом. Для каждой такой точки посчитаем разницу количества чёрных кубиков и количества белых кубиков, смежных с этой точкой. Что можно сказать про эту разницу?
Подсказка 17:
Вспомним условие и поймём, что она неположительна. Значит, сумма ∑ этих разностей по всем отмеченным точками также неположительна. Понятно, что какой-то конкретный маленький кубик мы учли несколько раз в ∑. Что тогда полезно было бы сделать?
Подсказка 18:
Ввести обозначение для количества отмеченных вершин конкретного кубика. Назовём эту величину кратностью. Воспользуемся техникой двойного подсчёта. Как же теперь с помощью новых обозначений можно посчитать ∑?
Подсказка 19:
Разумеется, ∑ = сумма всех кратностей чёрных кубиков — сумма кратностей белых кубиков. Итого, опираясь на некоторую "интуицию", мы ввели много обозначений и что-то поняли про ∑. Кажется, пришло время вновь немного поисследовать, посмотреть случаи. Рассмотрим произвольный кубик 2×2×2, пусть ранги его центра — r_x, r_y, r_z. Для однозначности будем считать, что r_x ≤ r_y ≤ r_z. Разберём несколько случаев.
Подсказка 20:
1) r_x < ry;
2) r_x = r_y = 1/2 + d, где d — чётно;
3) r_x = r_y = 1/2 + d, где d — нечётно.
Аккуратно разберите каждый случай и осознайте, что кратности всех тёмных кубиков не больше 4, а всех светлых — не меньше 4 (именно тёмных и светлых, а не чёрных и белых). Отличное продвижение. Давайте теперь для удобства введём обозначения кратностей: s₁ ≤ s₂ ≤ ... ≤ s_{(2N+1)³} С учётом продвижения и построенного примера, что можно сказать про эти кратности?
Подсказка 21:
Что s₁ + ... + s_{(N+1)²(4N+1)} = s_{(N+1)²(4N+1)+1} + ... + s_{(2N+1)³}, так как в примере ∑ = 0. Фух, осталось совсем немного. Осталось красиво завершить оценку противоречием. Пусть в раскраске чёрных кубиков > (N+1)²(4N+1). Что тогда?
Подсказка 22:
0 ≥ ∑ > s₁ + ... + s_{(N+1)²(4N+1)} − s_{(N+1)²(4N+1)+1} − ... − s_{(2N+1)³} = 0. В этой цепочке неравенств есть одно упущение (осознайте какое и допишите его, не забудьте обосновать). В итоге мы получили, что 0 > 0, если кубиков > (N+1)²(4N+1). Кажется, это победа)
Положим Введём систему координат так, что все вершины единичных кубиков будут иметь целые координаты от 0
до
Начнём с примера, показывающего, что количество чёрных кубиков действительно может быть равно У каждого кубика рассмотрим
его вершину, ближайшую к началу координат (её координаты принимают значения от 0 до
). Пусть кубик чёрный, если хотя бы две
координаты этой вершины чётны, и белый иначе. Ясно, что тогда в любом кубе
будет ровно 4 чёрных и 4 белых кубика. При
этом количество чёрных кубиков, у которых все три соответствующих координаты чётны, равно
а количество
кубиков, у которых чётны ровно две координаты, равно
поэтому общее количество чёрных кубиков будет равно
Осталось доказать, что этот пример оптимальный. Пусть куб сложен из чёрных и белых кубиков так, что выполнены условия задачи. Назовём кубик тёмным или светлым, если он является соответственно чёрным или белым в приведённом выше примере.
Для каждой точки с координатами в большом кубе назовём её
- и
-рангом соответственно числа
Назовём рангом этой точки число Иначе говоря,
- или
-ранг точки — это расстояние от неё до ближайшей
грани большого куба, перпендикулярной соответствующей оси, а её ранг — это просто расстояние от неё до ближайшей грани большого
куба.
Отметим все вершины единичных кубиков с нечётными рангами. Для каждой отмеченной вершины рассмотрим разность количеств
чёрных и белых кубиков, сходящихся в этой вершине; поскольку все эти вершины являются центрами кубов эта разность
неположительна. Значит, и сумма
всех таких разностей неположительна.
Скажем, что кратность единичного кубика — это количество его отмеченных вершин (столько раз этот кубик учтён в ).
Тогда
равна разности суммы всех кратностей чёрных кубиков и суммы кратностей всех белых кубиков. Поэтому
нам достаточно доказать, что если такая разность неположительна, то количество чёрных кубиков
не превосходит
Пусть
и
— это
-,
- и
-ранги центра некоторого кубика; пусть для определённости
Тогда нетрудно
видеть, что
- если
то кратность этого кубика равна 4;
-
если
где
чётно, то кратность кубика меньше 4, и он тёмный;
-
если
где
нечётно, то кратность кубика больше 4, и он светлый.
Итак, кратности всех тёмных кубиков не больше 4, а всех светлых — не меньше 4.
Пусть теперь
— кратности всех кубиков, расположенные в неубывающем порядке. Из сказанного выше вытекает, что
поскольку в приведённом выше примере значение было равно 0.
Если теперь в рассматриваемой раскраске чёрных кубиков, то
поскольку Это противоречие показывает, что
что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
По кругу выписаны 100 единиц. Петя и Вася играют в игру, каждый делает по ходов. Петя каждым своим ходом выбирает 9
стоящих подряд чисел и уменьшает каждое из них на 2. Вася каждый своим ходом выбирает 10 стоящих подряд чисел
и увеличивает каждое из них на 1. Ребята ходят по очереди, начинает Петя. Докажите, что Вася сможет действовать
так, чтобы после каждого его хода среди 100 выписанных чисел было не менее пяти положительных, как бы ни играл
Петя.
Источники:
Подсказка 1:
Нам нужно гарантировать 5 положительных чисел в любой момент. Есть несколько способов доказывать подобные утверждения. Первый способ: для любого момента доказать, что эти 5 чисел где-то найдутся, то есть просто доказать их существование. Второй способ: построить некоторый алгоритм ходов за Васю, зафиксировав некоторые числа, и доказать, что в любой момент именно они будут подходить (ну либо какие-то из них). Что же нам выбрать?
Подсказка 2:
Предпочтительнее для нас второй способ. Объясню почему. Доказывать существование нужно через какие-то оценки, общие суммы и так далее. Но мы смотрим на числа в целом, а в целом ходы Пети гораздо сильнее уменьшают общую сумму, нежели ходы Васи, поэтому через много ходов с помощью общих сумм и оценок мы просто не сможем доказать существование положительных чисел. Итого хотим найти некоторый набор чисел, который нам будет подходить в каждый момент.
Подсказка 3:
Доказывать, что какое-то число будет всегда положительным — гиблый номер, ибо Петя может с лёгкостью этому помешать. Если с одним числом не получилось, стоит рассмотреть пару...
Подсказка 4:
Попробовать доказать, что в какой-то паре при заданной стратегии хотя бы одно число будет положительным, уже не кажется плохой идеей. Однако пару тоже можно взять не любую...
Подсказка 5:
Если между числами из пары будет менее 8 чисел, то вновь Петя может всё испортить, так как одним ходом может уменьшить оба числа. Что же с парой чисел, между которыми ровно 8 других?
Подсказка 6:
Петя задевает ровно одно число из пары, в то время как Вася может прибавлять 1 сразу к обоим. Что тогда можно сказать про общую сумму в паре?
Подсказка 7:
Вася может сделать так, чтобы она не уменьшалась. А изначально сумма в паре положительна. Кажется, стратегия за Васю напрашивается сама собой, осталось найти 5 нужных пар. Успехов!
Обозначим записанные по кругу числа
…,
Вася будет следить лишь за десятью числами, которые он разобьёт на пары:
…,
За один ход Петя может уменьшить не более, чем одно из этих 10 чисел. Если Петя
уменьшил одно из чисел пары
Вася в ответ добавит 1 к числам
…,
Если же Петя не уменьшил
ни одно из этих 10 чисел, Вася сделает любой разрешённый ход. Таким образом, после пары ходов Пети и Васи сумма
чисел в каждой из пяти Васиных пар не уменьшится. Поскольку изначально пять сумм в парах положительны, то после
каждого Васиного хода сумма в каждой из этих пяти пар будет положительной, поэтому в каждой из пар будет хотя бы
одно положительное число. Таким образом, после любого Васиного хода будет хотя бы 5 положительных чисел, что и
требовалось.
Ошибка.
Попробуйте повторить позже
Четырёхугольник в котором нет параллельных сторон, вписан в окружность
В треугольники
вписаны окружности
соответственно. Проведены общие внешние касательные к окружностям
и
и
и
и
не содержащие сторон четырёхугольника
Четырёхугольник, последовательные стороны которого лежат на
четырёх проведённых прямых (именно в таком порядке), вписан в окружность
Докажите, что прямые, соединяющие центры
окружностей
и
и
и
пересекаются в одной точке.
Источники:
Пусть, не умаляя общности, лучи и
пересекаются в точке
лучи
и
пересекаются в точке
Обозначим через
центр окружности
точки
определим аналогично.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Четырехугольник является прямоугольником, стороны которого параллельны биссектрисам внутренних углов
и
Доказательство. Докажем, что прямая параллельна биссектрисе внутреннего угла
Действительно, пусть и
— середины дуг
и
не содержащие остальные вершины четырехугольника,
соответственно. Тогда в силу леммы о трезубце
но прямая
является биссектрисой угла
поэтому
.png)
С другой стороны, углы между парами прямых и
равны полусуммам пар дуг
и
а значит,
равны, следовательно,
перпендикулярна биссектрисе угла
Аналогично,
параллельна последней.
.png)
Как известно, биссектрисы внутренних углов перпендикулярны, следовательно, четырехугольник
суть прямоугольник,
поскольку пары его противоположных стороны параллельны биссектрисам.
_________________________________________________________________________________________________________________________________________________________________________________
Перейдем к решению. Таким образом, в силу доказанной леммы точка пересечения прямых является центром
описанной окружности
прямоугольника, т.е. достаточно показать, что окружности
имеют общую радикальную
ось.
Обозначим четырёхугольник, образованный четырьмя касательными через (прямая
— общая внешняя касательная к
и
аналогично с тремя другими сторонами). Пусть прямая
пересекает прямую
в точке
Точки обозначим через
описанную окружность четырёхугольника
Тогда точка — радикальный центр окружностей
и
поскольку она лежит на двух их радикальных осях. Значит,
радикальная ось окружностей
и
проходит через точку
аналогично, на ней лежат и точки
В частности, эти 4
точки лежат на одной прямой.
.png)
Пусть прямая пересекает сторону
в точке
и сторону
в точке
Поскольку
то
поэтому четырёхугольник
— вписанный. Поскольку
и
то по теореме
Фалеса
Из этого равенства отношений и вписанности мы получаем, что
то есть степень точки относительно окружностей
и
одинакова. Рассуждение для точек
аналогично. Итого
доказано требуемое утверждение.
.png)
Ошибка.
Попробуйте повторить позже
Пусть — непрерывная функция. Хордой будем называть отрезок целой длины, параллельный оси абсцисс, концы которого лежат
на графике функции
Известно, что у графика функции
ровно
хорд, причём среди них есть хорда длины 2025. Найдите
наименьшее возможное значение
Источники:
Для натурального положим
Тогда число хорд длины
равно количеству нулей функции
В качестве примера выберем следующую кусочно-линейную функцию :
при
и
при Заметим, что при
функция
принимает значение
только в точке
Следовательно, если
то обе точки
и
лежат в отрезке
В частности,
и нули функции
лежат в промежутке
Для
при
имеем
Значит,
имеет единственный нуль
то есть
хорда длины 2025 у функции
единственна. При натуральном
функция
монотонно убывает при
и
монотонно возрастает при
при этом
Таким образом, у этой
функции ровно два нуля, то есть функция
имеет по две хорды длины
Итого у неё 4049 различных
хорд.
Теперь перейдём к оценке. Без ограничения общности будем считать, что хорда длины 2025 соединяет точки и
то есть
Положим
Из условия следует, что у функции конечное число нулей, а также эта функция непрерывна. Пусть все её нули лежат в промежутке
Тогда функция
знакопостоянна на лучах
и
При необходимости, заменив функцию
на
будем
считать, что
при
Предположим, что при
Заметим, что
поэтому при
и
при
Значит, функция
имеет нуль, то есть у функции
есть хорда
любой натуральной длины, что противоречит условию.
Таким образом, при
Значит,
при
и при
Далее мы докажем, что при натуральных
и
в сумме дающих 2025, функция
имеет хотя бы 4 хорды длин
и
Применяя это утверждение для каждой такой
пары, получим оценку. Иными словами, докажем, что у функций
и
при
суммарно хотя бы 4
нуля.
Предположим, что это не так. Тогда функция имеет не более одного нуля. Значит,
не может быть отрицательной.
Действительно, если
то по непрерывности и знакам при больших
функция имеет хотя бы два нуля, противоречие.
Итого причём равенство нулю достигается не более чем в одной точке. Покажем, что
для некоторого
Рассмотрим наименьшее натуральное
для которого
делится на 2025, и обозначим остатки
…,
от деления чисел
…,
по модулю 2025. Если
положим
если
положим
Рассмотрим
разности
Если то
и
если же
то
и
Если
то
В случае
получаем
поскольку
и
Таким
образом,
и одно из крайних слагаемых положительно. Значит, найдётся что возможно только при
и
Тогда для
получаем
Заметим, что
Поскольку то
и
в частности,
и
то есть
В случае
и
получаем
а также
при больших
Тогда у
есть нули на промежутках
то есть хотя бы 4 нуля.
Если то
так как у
не более одного нуля. Тогда
В этом случае у
есть
нули на
и
а также в точке
и ещё один нуль в точке
есть у
что даёт хотя бы 4 нуля. Случай
разбирается аналогично.
4049
Ошибка.
Попробуйте повторить позже
Квартал представляет собой клетчатый квадрат В новогоднюю ночь внезапно впервые пошёл снег, и с тех пор
каждую ночь на каждую клетку выпадало ровно по 10 см снега; снег падал только по ночам. Каждое утро дворник выбирает
один ряд (строку или столбец) и сгребает весь снег оттуда на один из соседних рядов (с каждой клетки — на соседнюю по
стороне). Например, он может выбрать седьмой столбец и из каждой его клетки сгрести снег в клетку слева от неё. Сгребать
снег за пределы квартала нельзя. Вечером сотого дня года в город приедет инспектор и найдёт клетку, на которой лежит
сугроб наибольшей высоты. Цель дворника — добиться, чтобы эта высота была минимальна. Сугроб какой высоты найдёт
инспектор?
Источники:
Подсказка 1.
Хочется верить, что в оптимальном примере во всех непустых ячейках почти поровну снега.
Будем измерять высоту сугроба в дециметрах. Также будем считать, что сторона одной клетки равна дм, то есть за каждую ночь на
клетку выпадает
снега.
Докажем, что после сотого утра найдется сугроб высотой не менее дм. Предположим, что такого сугроба нет. Так как дворник в
сотое утро полностью сгреб снег с какого-то ряда, в десяти клетках квадрата снега нет. В каждой из оставшихся
клеток, по нашему
предположению, не более
снега, то есть всего снега не больше, чем
Однако за
ночей суммарно выпало
снега. Противоречие.
Покажем, как может действовать дворник, чтобы после сотого утра каждый сугроб имел высоту не более дм, то есть в каждой
клетке было не более
снега.
Способ 1. Первые дней дворник сгребает снег из второго столбца в первый, следующие
дней дворник сгребает снег из
третьего столбца во второй, затем
дней из четвёртого в третий, и т. д. Через
дней в десятом столбце не будет
снега. Посчитаем, сколько снега стало в столбце
через
дней. Вечером
-го дня в столбце номер
не
было снега, а в столбце
в каждой клетке было по
снега. На следующий вечер в столбце
станет
по
снега в каждой клетке. Затем ещё десять дней количество снега в каждой клетке
-го столбца
будет увеличиваться на
а затем
дней — на
Итого, через
дней в каждой клетке столбца
будет
по
В сотую ночь выпадет ещё по
в каждую клетку. А сотым утром дворник сгребёт снег из десятого столбца в девятый. Таким
образом, в каждой клетке будет не более
снега.
_________________________________________________________________________________________________________________________________________________________________________________
Способ 2. Пусть дворник сгребёт снег из -го столбца в
-ый, из
-го во
-й, …, из
-го в
-ый. Тогда вечером девятого дня в
первых девяти столбцах будет по
дм
снега в каждой клетке, а в десятом столбце снега не будем. Затем дворник проделывает
аналогичный процесс в обратном порядке: из
-го в
-ый, из
-го в
-ый, …, из
-го в первой. Тогда вечером
-го дня в клетках
последних девяти столбцов будет по
снега, а в первом столбце не будет снега. Аналогично повторим такие сдвиги (каждый длится
дней) ещё
раз (всего
сдвигов), и через
дней получим в клетках девяти столбцов по
снега и один крайний
столбец пустой. Сотым утром сгребаем снег из этого крайнего в соседний и получаем не более
снега в каждой
клетке.
1120 см
Ошибка.
Попробуйте повторить позже
В пространстве расположен бесконечный цилиндр (т.е. геометрическое место точек, удалённых от данной прямой на данное расстояние
). Могут ли шесть прямых, содержащих рёбра некоторого тетраэдра, иметь ровно по одной общей точке с этим
цилиндром?
Источники:
Подсказка 1:
В таких задачах бывает полезно сначала потыкаться в пример. Казалось бы, почему такой ситуации не может быть?
Подсказка 2:
Спустя конечное число попыток вы, скорее всего, столкнулись с рядом проблем. Это значит, что пора задуматься о противоположном ответе...
Подсказка 3:
Когда мы строим пример, 4 прямые удаётся расположить нужным образом, с остальными же начинаются проблемы. Как бы доказать, что проблемы будут всегда?
Подсказка 4:
Можно рассуждать в пространстве (и так задача, действительно, убивается). Однако в стереометрии часто бывает полезно применить технику проецирования. На какую же плоскость хочется проецировать больше всего, чтоб цилиндр перешёл в адекватный объект?
Подсказка 5:
Либо на ту, которая содержит ось цилиндра, либо на ту, которая перпендикулярна ей. В первом случае цилиндр станет двумя параллельными прямыми, в другом — окружностью. Какой же случай нравится нам больше, учитывая, что мы рассуждаем о касаниях?
Подсказка 6:
Разумеется, второй. Пусть A, B, C, D — образы вершин тетраэдра после проецирования. Подумаем, чем стали прямые, содержащие рёбра?
Подсказка 7:
Прямыми! Осознайте, что никакая такая прямая не могла спроецироваться в точку. Что же дальше? Подумаем, могли ли какие-нибудь образы вершин попасть на одну прямую?
Подсказка 8:
Могли, но не более 3 (подумайте почему). То есть, не умоляя общности, можно сказать, что прямые AB, AC, AD различны. Ничего не смущает?...
Подсказка 9:
Они же все касаются окружности (образа цилиндра) и имеют общую точку. Кажется, такое бывает примерно никогда) Успехов!
Предположим, что такая конструкция существует. Спроецируем тетраэдра на плоскость перпендикулярную прямой
Проекцией
цилиндра будет некоторая окружность
Обозначим проекции вершин тетраэдра через
они все будут
различны (в противном случае одна из прямых, содержащих стороны тетраэдра, будет параллельна
такая прямая не
может иметь с цилиндром ровно одну общую точку). Каждая из прямых, соединяющих точки
должна
иметь с окружностью
одну общую точку, то есть касаться этой окружности. При этом точки
не могут
лежать на одной прямой (поскольку вершины тетраэдра не лежат в одной плоскости). Значит, либо на одной прямой лежат
какие-то три из них, не умаляя общности
либо никакие три из этих точек на одной прямой не лежат. В любом
случае прямые
попарно различны, однако они все касаются окружности
и проходят через точку
противоречие.
.png)
не могут
Ошибка.
Попробуйте повторить позже
Тройку положительных чисел назовём загадочной, если
Докажите, что если тройка — загадочная, то тройка
— тоже загадочная.
Источники:
Подсказка 1
Рассмотрите условие загадочности. Попробуйте свести сложное равенство к более простому условию на a, b, c.
Подсказка 2
Проанализируйте первое подкоренное выражение: a² + 1/(a²c²) + 2ab. Заметьте: если бы 1/(a²c²) равнялось b², то получился бы полный квадрат. Что в этом случае можно сказать о загадочности тройки?
Подсказка 3
Если abc = 1, то b = 1/(ac) ⇒ b² = 1/(a²c²). Тогда, сворачивая полные квадраты в подкоренных выражениях, получаем загадочное равенство. Можно ли похожие преобразования провести в случаях неравенства?
Подсказка 4
Если abc < 1, то b < 1/(ac) ⇒ b² < 1/(a²c²). Можно ли и дальше проводить преобразования аналогично случаю для равенства, меняя "=" на знак неравенства?
Подсказка 5
Если abc > 1, то b > 1/(ac) ⇒ b² > 1/(a²c²). Получим: √(a² + 1/(a²c²) + 2ab) < √(a² + b² + 2ab) = a + b. Как это повлияет на всю сумму?
Подсказка 6
Загадочное равенство достигается только при abc = 1. Почему это доказывает, что (c, b, a) тоже загадочная тройка?
Покажем, что тройка — загадочная в том и только в том случае, когда
из этого немедленно последует требуемое в
задаче.
Пусть тогда
ведь положительны. Аналогично
из этого следует, что тройка замечательная.
Предположим, что Тогда
и аналогично случаю для равенства, получаем неравенство:
аналогично
Итого, в этом случае левая часть равенства из условия больше правой. Рассуждая аналогично, в случае имеем, что правая
часть больше левой, и только в случае
достигается равенство, что и требовалось.
Ошибка.
Попробуйте повторить позже
Юрий подошёл к великой таблице майя. В таблице 200 столбцов и строк. Юрий знает, что в каждой клетке таблицы изображено
солнце или луна, и любые две строки отличаются (хотя бы в одном столбце). Каждая клетка таблицы закрыта листом. Поднялся ветер и
сдул некоторые листы: по два листа с каждой строки. Могло ли так случиться, что теперь Юрий хотя бы про 10000 строк может узнать, что
в каждой из них изображено в каждом из столбцов?
Источники:
Подсказка 1.
Сейчас для нас главная сложность — понять, делать оценку или пример. Так вот, рассмотрите аналог задачи для маленьких чисел, чтобы понять это.
Заметим, что существует всего различных строк длины
в которых каждый символ — солнце или луна; значит, каждая такая
строка встречается в таблице ровно один раз. Разобьём все позиции на две половины по
столбцов — «левую» и «правую».
Предположим, что в каждой строке, в которой есть два солнца в одной половине (назовём их солнечными), ветер сдул листья с одной из
таких пар солнц, а в каждой несолнечной строке — таких строк
— ветер обнаружил положения всех солнц, ведь в несолнечной строке
не более двух солнц, так что ветер мог так поступить. Тогда Юрий сообразит, что те строки, где открыты два солнца в одной
половине — точно солнечные, а значит, несолнечные строки — это в точности те
строк, в которых ветер не открывал два
солнца в одной половине. У каждой из них открыты все солнца, так что закрытые листьями изображения в этих строках —
луна.
могло
Ошибка.
Попробуйте повторить позже
Четырёхугольник в котором нет параллельных сторон, вписан в окружность
Через вершину
проведена прямая
через вершину
— прямая
через вершину
— прямая
через вершину
— прямая
Четырёхугольник,
последовательные стороны которого лежат на этих четырёх прямых (именно в этом порядке), вписан в окружность
Окружности
и
пересекаются в точках
и
Докажите, что прямые
и
пересекаются в одной
точке.
Источники:
Подсказка 1.
Если в задачах с окружностями требуется доказать, что 3 прямые пересекаются в одной точке, часто помогает найти 3 окружности, радикальными осями которых являются эти прямые. К тому же в нашей задаче EF определяется как радикальная ось каких-то окружностей.
Первое решение. Без ограничения общности можно считать, что лучи и
и
пересекаются. Пусть отрезки
и
пересекаются в точке
а также
— четырёхугольник, образованный прямыми
Также обозначим через
пересечение
и
через
— пересечение
и
Пусть Из вписанности четырёхугольника
и условий
имеем:
Значит, во-первых, точки
лежат на одной окружности, обозначим её
во-вторых, точки
лежат на
одной окружности, обозначим её
в-третьих, точки
лежат на одной окружности, обозначим её
Заметим, что точка
— радикальный центр окружностей
(поскольку она лежит на прямых
и
точка
— радикальный центр
окружностей
(так как она лежит на прямых
и
Таким образом,
— радикальная ось окружностей
и
—радикальная ось окружностей
и
— радикальная ось окружностей
и
поэтому эти три прямые пересекаются в
одной точке, что и требовалось доказать.
.png)
Второе решение. Введём обозначения как в первом решении. Для точки плоскости обозначим через
разность степеней точки
относительно окружностей
и
Поскольку
— радикальная ось окружностей
и
то достаточно доказать, что
Кроме того, легко видеть, что
и
Заметим, что функция — линейная, то есть для точки
на отрезке
выполнено равенство
Мы докажем это утверждение позднее. Пока, применив его для точек мы получим, что
Таким образом, достаточно доказать, что
Заметим, что
(последнее равенство следует из того, что через
мы обозначаем расстояние от точки
до прямой
Следовательно, равенство (
) переписывается в виде:
Из вписанности четырёхугольника и данных в условии параллельностей прямых следуют равенства углов:
Таким образом, и
а также
и
подобны по двум углам. Из подобия получаем равенства
отношений
остаётся лишь перемножить эти равенства.
.png)
Вернёмся к доказательству линейности функции Введём декартовы координаты таким образом, чтобы центры окружностей
и
лежали на оси абсцисс, пусть их координаты будут
и
а радиусы окружностей
и
Тогда для произвольной точки
с координатами
по определению степени точки мы получаем, что
где и
— две константы. Если точка
лежит на отрезке
и
,
— координаты точек
и
по оси абсцисс, то
откуда немедленно следует (*).
Ошибка.
Попробуйте повторить позже
Остроугольный неравнобедренный треугольник вписан в окружность
с центром в точке
его высоты пересекаются в точке
Через точку
проведена прямая, перпендикулярная
а через точку
— прямая, перпендикулярная
Докажите, что
точки пересечения этих прямых со сторонами
и
лежат на одной окружности, которая касается окружности
Источники:
Подсказка 1.
Для начала докажем, что эти 4 точки лежат на одной окружности счётом углов. Какие существуют способы доказательства касания двух окружностей?
Подсказка 2.
Основным способом является угадывание точки касания. У неё должен быть какой-то способ построения, поэтому есть смысл рассмотреть частные случаи, чтобы понять побольше про него.
Подсказка 3.
Например, разберите случаи AB=AC и ∠B=90°.
Подсказка 4.
В случае AB=AC видим, что точка касания лежит на AH, причём она совпадает или с A, или с диаметрально противоположной A. В случае же ∠B=90° получаем, что точка касания лежит на AH (даже совпадает с H), причём не совпадает с A. На какую мысль это может натолкнуть?
Подсказка 5.
Хочется выдвинуть гипотезу того, что точка касания D — второе пересечение AH с описанной окружностью ABC. Тем более у неё есть множество хороших свойств.
Подсказка 6.
Сначала докажем, что D лежит на искомой окружности. Заметим, что A и D симметричны относительно XY, H и D симметричны относительно BC. Отсюда можем получить различные равенства углов.
Подсказка 7.
Получим, что ∠XYD = ∠BHD, тогда остаётся доказать, что BZHD вписан. Сделайте это несложным счётом углов.
Подсказка 8.
А теперь докажите, что описанная окружность DXY касается описанной окружности ABC, учитывая, что D и A симметричны относительно XY.
Пусть прямая повторно пересекает окружность
в точке
Тогда прямая, проведённая по условию через
— серединный
перпендикуляр к хорде
пусть она пересекает стороны
и
в точках
и
а прямая через
из условия задачи пересекает
их в точках
и
Поскольку
то окружность
касается окружности
в точке
При симметрии относительно
окружность
переходит в себя, а окружность
переходит в окружность
тогда она тоже касается окружности
.png)
Поскольку то
Следовательно, четырёхугольник — вписанный. Тогда
Значит, в силу сказанного выше,
поэтому точка лежит на окружности
Аналогично, на этой окружности лежит и точка
откуда и следует
требуемое.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Можно рассуждать несколько иначе: установить (похожими равенствами углов), что точки лежат на одной
окружности, а также что окружности
и
касаются окружности
в точке
Однако эти три окружности не могут быть
различными, поскольку в таком случае их радикальные оси не пересекаются в одной точке, в чём нетрудно убедиться. Значит, все эти
окружности совпадают, что нам и требовалось.
Ошибка.
Попробуйте повторить позже
В стране городов и пока нет дорог. Правительство наугад определяет стоимость строительства дороги (с двусторонним движением)
между каждыми двумя городами, используя по разу все суммы от 1 до
талеров (все варианты равновероятны). Мэр каждого
города выбирает самую дешёвую из
возможных дорог, идущих из этого города, и она строится (это может быть взаимным желанием
мэров обоих соединяемых городов или только одного из двух).
После строительства этих дорог города оказываются разбиты на компонент связности (между городами одной компоненты связности
можно добраться по построенным дорогам, возможно, с пересадками, а между городами разных компонент — нельзя). Найдите
математическое ожидание случайной величины
Источники:
Подсказка 1
Дороги с какой стоимостью точно будут построены? Рассмотрите дороги, которые строятся по взаимному желанию обоих мэров (назовём их надёжными). Сколько всего таких дорог может быть?
Подсказка 2
Может ли существовать путь между двумя такими дорогами? Не противоречит ли его существование правилам, по которым мэры выбирают дороги для строительства?
Подсказка 3
Из предыдущего следует: число компонент M равно числу надёжных дорог. Как найти математическое ожидание? Вспомните линейность математического ожидания. На какие простые случайные величины стоит разложить M?
Подсказка 4
Введите для каждой пары городов {A,B} индикатор ξ(AB) = 1 (если AB — надёжная дорога), иначе 0. Тогда M — это сумма индикаторов по всем парам. Чему равно математическое ожидание одного из них?
Подсказка 5
Для фиксированной пары {A,B}: AB надёжна ⇔ AB дешевле всех дорог, инцидентных A или B. Сколько таких дорог? Зная их количества и равномерное распределение цен, можно подсчитать вероятность, что дорога AB надежна.
Дорогу, которую хотят строить сразу два мэра, назовём надёжной. Рассмотрим в каждой компоненте самую дешёвую дорогу Тогда
она является надёжной. Предположим, что в этой компоненте есть ещё одна надёжная дорога
(ясно, что города
отличны от
) и рассмотрим путь по дорогам от одного из городов
до одного из городов
— не
умаляя общности, он имеет вид
(города
отличны от
возможно,
).
Тогда дорогу
хочет строить мэр города
(мэр города
хочет строить
), дорогу
— мэр города
(мэр города
хочет строить
) и так далее, мэр города
хочет строить дорогу
а не
—
противоречие.
Итак, в каждой компоненте есть ровно одна надёжная дорога. Для каждой из пар городов
рассмотрим случайную
величину
которая равна
если
— надёжная дорога, и 0 в противном случае. Из доказанного следует, что
есть сумма
по всем
парам
Для данных
событие
означает, что дорога
— самая дешёвая из
дорог, выходящих из
или
так что вероятность такого события равна
(из симметричности распределения цен эти дороги
равноправны, так что каждая из них является самой дешёвой с вероятностью
). Значит, математическое ожидание
равно
а математическое ожидание случайной величины
равно сумме этих математических ожиданий по всем парам, то
есть
Ошибка.
Попробуйте повторить позже
Докажите, что существует такое что для любого нечётного простого
числа
…,
дают хотя бы
различных остатков при делении на
Источники:
Все сравнения в этом решении производятся по модулю Если
и
— целые числа, причём
не делится на
то через
мы
обозначаем тот единственный остаток
по модулю
для которого
Пусть числа
дают ровно различных остатков при делении на
Обозначим
Тогда выражения вида
при дают максимум
различных остатков.
Назовём пару натуральных чисел таких, что
исключительной, если
Покажем, что для каждого
существует не более одной исключительной пары
в которой
Действительно, если
— такая
пара, то из
вытекает, что
откуда
или Такой остаток
не более чем единственен (поскольку
), а по нему восстанавливается
Итого, существует не более чем исключительная пара; обозначим их количество через
Пусть числа
дают
ровно
различных остатков по модулю
встречающихся
раз соответственно. Тогда
Верна следующая цепочка неравенств:
откуда
Вспоминая, что получаем оценку
Таким образом, в качестве искомой константы можно взять, например, число
для простых
неравенство
тривиально, а для
следует из неравенства
при
Ошибка.
Попробуйте повторить позже
У школьников есть стопка из
карточки, которые пронумерованы числами от
до
Первый школьник перемешивает стопку,
затем берет сверху из получившейся стопки по одной карточке, и при каждом взятии карточки (в том числе при первом) записывает на
доску среднее арифметическое чисел на всех взятых им на данный момент карточках. Так он записывает
чисел, а когда в стопке
остается одна карточка, он возвращает карточки в стопку, и далее все то же самое, начиная с перемешивания стопки,
проделывает второй школьник, потом третий, и т.д. Докажите, что среди выписанных на доске
чисел найдутся два
одинаковых.
Источники:
Подсказка 1
Попробуйте посмотреть, какие множества чисел могут получаться у школьников на 1 шаге, на 2 шаге, на 100 шаге?
Подсказка 2
Попробуйте в явном виде найти все возможные значения, находящиеся в этих множествах. Как найти одинаковые среди них?
Подсказка 3
Рассмотрите первое, второе и сотое множества, а именно их объединение. Сколько в нëм чисел?
На -м шаге у каждого из
человек было выписано одно из чисел множества
На -м шаге — одно из чисел множества
На -м шаге выписано одно из чисел множества
где — сумма всех чисел (а вычитается — число на оставшейся в конце карточке).
Видим, что так что
Далее,
но числа
принадлежат
значит,
Итак, мы показали, что чисел, выписанных на
-м,
-м и
-м шагах, могут принимать не более
различных значений.
Следовательно, какие-то два из них равны.
Ошибка.
Попробуйте повторить позже
Число таково, что
и
— рациональные числа. Докажите, что
является корнем квадратного уравнения
с целыми коэффициентами.
Источники:
Подсказка 1:
Ясно, что sin(2x) выражается через sin(x)cos(x). Если найти уравнение с таким корнем, то будет несложно получить корень sin(2x).
Подсказка 2:
Давайте заметим, что выражения a + b и ab будут целыми и инвариантными относительно перестановки синуса и косинуса. Почему бы в дополнение к выражению v = sin(x)cos(x) не взять выражение u = sin(x) + cos(x) и попробовать выразить ab и a + b через u и v?
Подсказка 3:
Вы должны были получить такие равенства: a + b = u + 1/v, ab = v + u + 1. Как из них получить нужное уравнение?
Положим и
Введём обозначения:
и
По условию рациональными являются числа
и
Отсюда
Значит,
является решением квадратного уравнения
с рациональными коэффициентами, откуда следует требуемое.
Ошибка.
Попробуйте повторить позже
В каждой строке таблицы в некотором порядке стоят числа от 1 до 100, числа в строке не повторяются (в таблице
строк и 100
столбцов). Разрешается поменять местами в строке два числа, отличающиеся на 1, если они не стоят рядом. Оказалось, что с помощью
таких операций нельзя получить двух одинаковых строк. При каком наибольшем
это возможно?
Источники:
Подсказка 1:
По условию нельзя одну строку перевести в другую. Что это означает в общем виде?
Подсказка 2:
Каждой строке присущ индивидуальный признак, над которым описанная операция невластна либо власть очень ограничена, то есть с помощью этой операции можно совсем немного изменить этот признак. Разумеется, нам будет проще, если признак будет абсолютно неприступным, ведь тогда гораздо проще делать оценку в силу "фиксированности". Попробуем сначала доказать именно это. Что это за особенность такая?
Подсказка 3:
Может быть, это какой-то арифметический признак? Какая-нибудь сумма квадратов разностей между соседними числами... Или что-нибудь другое?
Подсказка 4:
Спустя время можно осознать, что арифметика не особо-то и вяжется сюда. Значит, думаем дальше. Мы меняем два элемента с разницей в 1. Хмм, попробуем просто поисследовать, что происходит при операции. Например, можно начать с анализа соседних чисел с теми, которые мы меняем...
Подсказка 5:
Пусть последовательность выглядела так: ...abc...def.... Меняем b и e. Знаем, что |b − e| = 1. Интересно, может ли случиться так, что b > c, а e < c?
Подсказка 6:
Конечно, нет. Иначе b ≥ c + 1, e ≤ c − 1, то есть b − e ≥ 2, ошибочка однако... Хм, на какую более общую идею это наталкивает?
Подсказка 7:
Отношения (в плане больше или меньше) сохраняются при перестановке b и e. Кажется, мы на верном пути! Итак, какая же у нас идея?
Подсказка 8:
Если рассмотреть в какой-то строке отношения между всеми соседними, то оно всегда будет оставаться таким же! Хммм, как бы изящно записать эти отношения?
Подсказка 9:
Наверное, с помощью знаков < и >. То есть каждой строке сопоставляем такую последовательность из 99 знаков, назовём её признаком. Получается, если у двух строк разные признаки, то одну из другой не получить. А если совпадают, всегда ли можно?
Подсказка 10:
Оставим это подзадачу для самостоятельного решения, но скажем одно: ответ положительный. Итак, теперь мы знаем, что строк в таблице не больше, чем количество различных признаков. Какую оценку мы тогда получили на n?
Подсказка 11:
n ≤ 2⁹⁹ (осознайте почему). Попробуем же теперь построить пример.
Подсказка 12:
В явном виде строить его довольно трудно. Нужно действовать хитрее! Зафиксируем признак и докажем, что для него можно подобрать нужный набор чисел (доказать это необходимо в общем виде). Это будет ещё одна подзадача для самостоятельного решения) Дело за Вами! Мы в Вас верим!
Сопоставим строке
…,
чисел от 1 до 100 последовательность из 99 знаков < и > в соответствии с тем, как упорядочены
соседние числа. То есть если
то
-й знак в этой последовательности равен <, в противном случае он равен
>.
Заметим, что разрешённые операции над строкой не меняют соответствующую ей последовательность знаков. Действительно, из пары
чисел и
меняется не более одного и не более чем на 1. Поэтому знак неравенства между ними не может измениться на
противоположный.
Сопоставим каждой перестановке знаков расстановку чисел по следующему правилу (далее такие расстановки будем называть
выделенными). При
…,
если
(т.е.
-й знак <) поставим на место
наибольшее из не выбранных ранее чисел,
если же
— наименьшее из не выбранных ранее чисел.
Заметим, что при такой последовательности операций числа, не выбранные за первые шагов, будут образовывать отрезок
натурального ряда (а выбранными окажутся несколько наибольших и несколько наименьших чисел от 1 до 100). В частности,
или
Число
заменим на единственное оставшееся число.
Нетрудно видеть, что полученная расстановка чисел соответствует выбранной последовательности знаков. Всего выделенных расстановок
будет столько же, сколько и различных последовательностей знаков, то есть В силу сказанного выше, разрешёнными операциями
никакие две из выделенных строк нельзя сделать одинаковыми. Таким образом, заполнив таблицу
выделенными строками, мы
получаем пример для
Теперь докажем, что из любой строки длины 100 можно получить выделенную строку
с той же расстановкой знаков. Из этого
последует, что
Предположим, что первые знаков данной строки
и выделенной строки
совпадают. Если то и сами строки совпадают. Пусть
Без ограничения общности будем считать, что
В силу сказанного выше наборы чисел …,
и
…,
совпадают и образуют отрезок натурального ряда с наименьшим
числом
Поскольку
можно менять в строке
на месте
с числом на единицу меньшим, пока на месте
не окажется
число
Таким образом, мы добились совпадения первых символов у нашей строки с выделенной строкой
Значит, такими операциями
можно из любой строки получить выделенную строку, что завершает доказательство оценки.
Ошибка.
Попробуйте повторить позже
Окружность описана около треугольника
в котором
Биссектрисы треугольника
пересекаются в точке
Из середины
стороны
на прямую
опущен перпендикуляр
Прямые
и
ограничивают треугольник
а прямые
и
ограничивают треугольник
Описанные окружности треугольников
и
повторно пересекают окружность
в точках
и
соответственно. Докажите, что точка
лежит на прямой
Источники:
Обозначим точки пересечения прямой с прямыми
и
через
и
соответственно (см. рисунок). Пусть
прямые
и
повторно пересекают
в точках
и
соответственно. Обозначим
тогда из суммы углов треугольника
Поскольку
имеем
Так как четырехугольник
— вписанный,
Таким образом,
поэтому четырёхугольник — вписанный. Следовательно,
откуда следует, что точки
лежат на
окружности
построенной на отрезке
как на диаметре.
Теперь заметим, что
Однако из вписанности четырехугольника мы получаем, что
Следовательно, точки
и
лежат на одной прямой. Аналогично, точки
и
лежат на одной прямой.
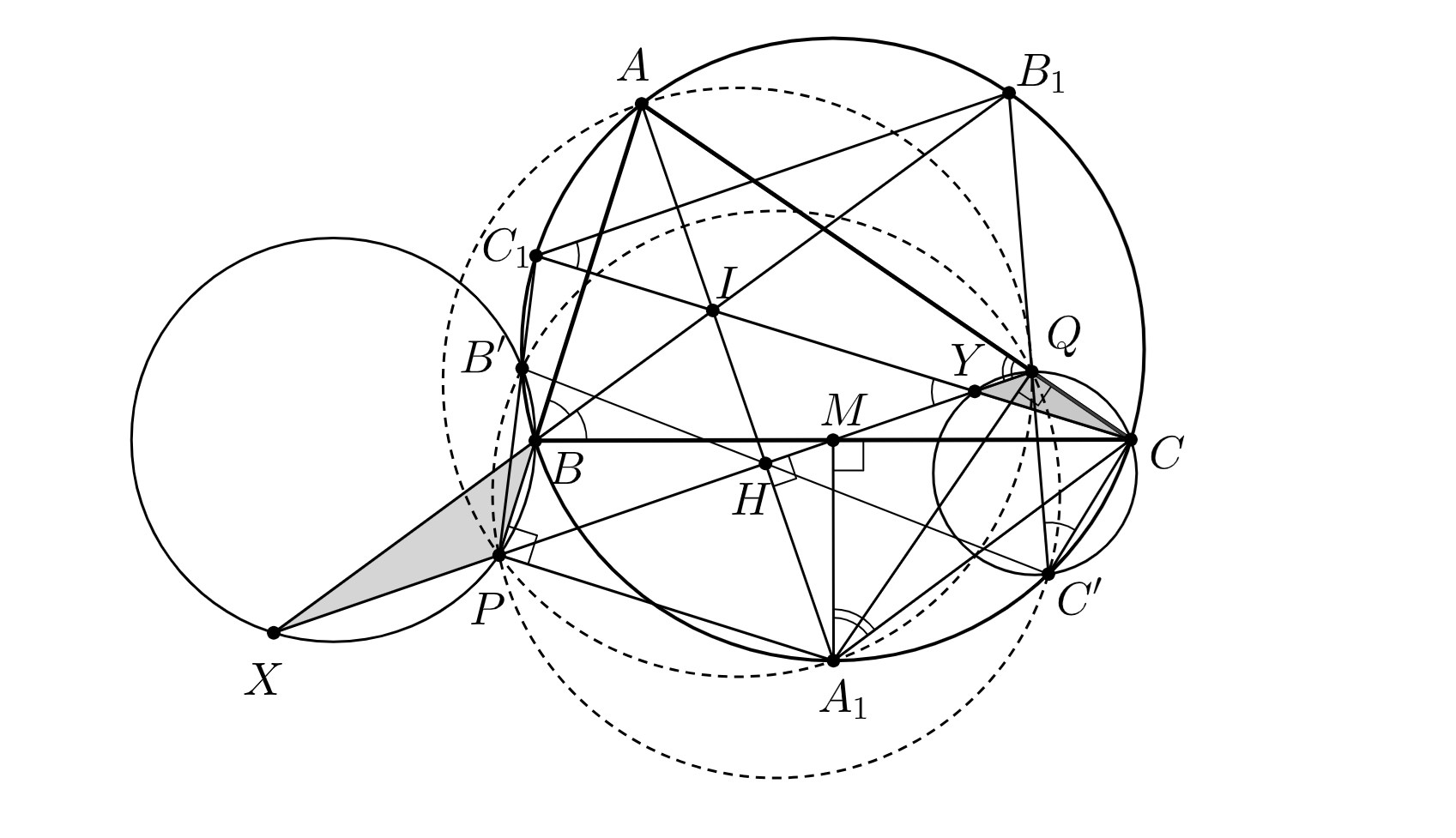
В силу сказанного выше и вписанности четырёхугольника имеем, что
поэтому Поскольку четырёхугольник
вписанный,
Значит, четырёхугольник вписанный. Тогда радикальные оси его описанной окружности, окружности
и окружности
пересекаются в одной точке, а это прямые
и
Следовательно, точка
лежит на прямой
что и требовалось
доказать.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Приведём другой способ закончить решение. После того, как установлено, что точки
и
лежат на одной прямой,
и точки
и
лежат на одной прямой. Обозначим через
середину дуги
Пусть прямая
повторно пересекает
окружность
в точке
Заметим, что
Следовательно, — биссектриса угла
поэтому на прямой
лежит точка
Аналогично, она лежит
на прямой
Применяя теорему Паскаля для точек
мы получаем, что точка
точка
и точка
пересечения
и
лежат на одной прямой. Следовательно, прямые
и
Т пересекаются в одной точке,
то есть точка
лежит на
Теперь применяем теорему Паскаля для точек
и получаем, что точки
и
вместе с точкой пересечения
и
лежат на одной прямой. Значит, точка
лежит на
что и
требовалось.



