Закл (финал) 11 класс

Зафиксируем точки Пусть точка движется линейно по прямой, проходящей через параллельно Тогда точка так же движется линейно, поскольку Кроме этого, является точкой пересечения серединных перпендикуляров к отрезкам (фиксирован при движении) и (имеет постоянное направление и проходит через середину отрезка которая движется линейно), следовательно движется линейно. Аналогично точка движется линейно.

Рассмотрим треугольник Заметим, что прямая фиксированная, поскольку является серединным перпендикуляром к фиксированному отрезку следовательно высота, проведенная из точки имеет постоянное направление, кроме этого проходит через линейнодвижущуюся точку. То же верно про высоту, проведенную из вершины Наконец, точка пересечения указанных прямых движется линейно. Покажем, что в двух положениях лежит на

Положение 1. Пусть точка такова, что является прямоугольником. Тогда является серединой стороны — Пусть — середина стороны Как известно, является ортоцентром треугольника а значит является ортоцентром треугольника и принадлежит

Положение 2. Пусть совпадает с В этом случае точка определяется как точка пересечения прямой, проходящей через и перпендикулярной и серединного перпендикуляра к точка симметрична относительной прямой

Заметим, что

что влечет принадлежность точек и одной окружности.

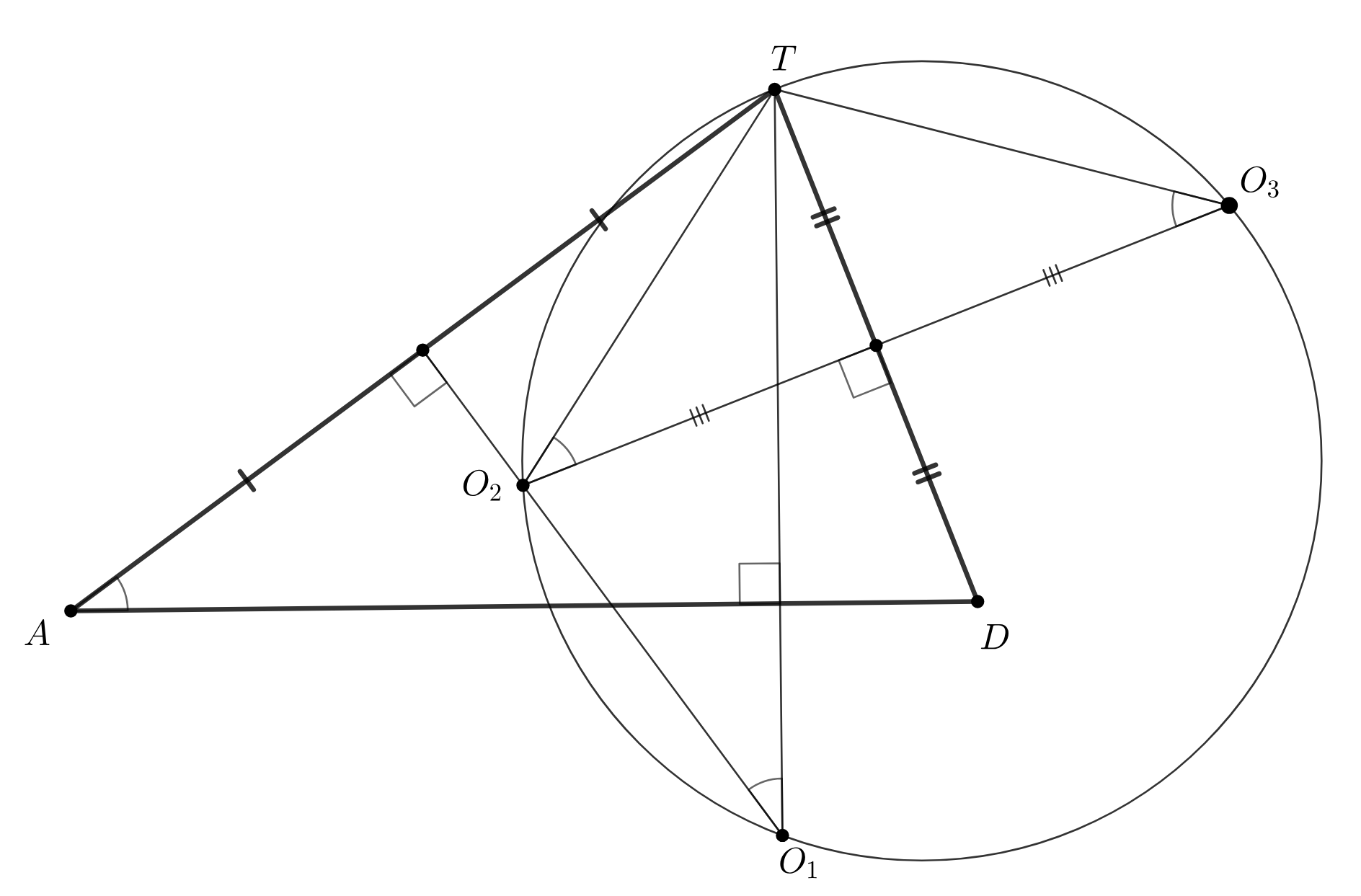
Наконец, точки и симметричны точке относительно одной из сторон треугольника , следовательно прямая является прямой Штейнера точки относительно треугольника и проходит через ее ортоцентр.