Закл (финал) 11 класс

Пронумеруем строки числами сверху вниз, а столбцы — теми же числами слева направо. Клетку будем обозначать парой номеров её строки и столбца; при этом будем считать, что клетки диагонали из плюсов имеют координаты

Заметим, что если четыре клетки лежат в вершинах прямоугольника со сторонами, параллельными осям координат, то любая операция либо не меняет знаков в этих клетках, либо меняет знаки ровно в двух клетках из четырёх. В частности, чётность количества плюсов в этих четырёх клетках не меняется; значит, если среди них вначале был ровно один плюс, то и потом их будет не менее одного.

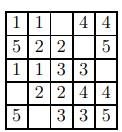
Теперь выберем в нашей таблице непересекающихся таких четвёрок; по сказанному выше, после любых операций в каждой из них найдётся как минимум один плюс, следовательно, всего плюсов будет не менее При выберем четвёрку клеток выберем четвёрку клеток а также выберем четвёрки и Легко видеть, что они удовлетворяют всем требованиям. На рисунке отмечены такие четвёрки при