.14 Сила Архимеда
Ошибка.
Попробуйте повторить позже
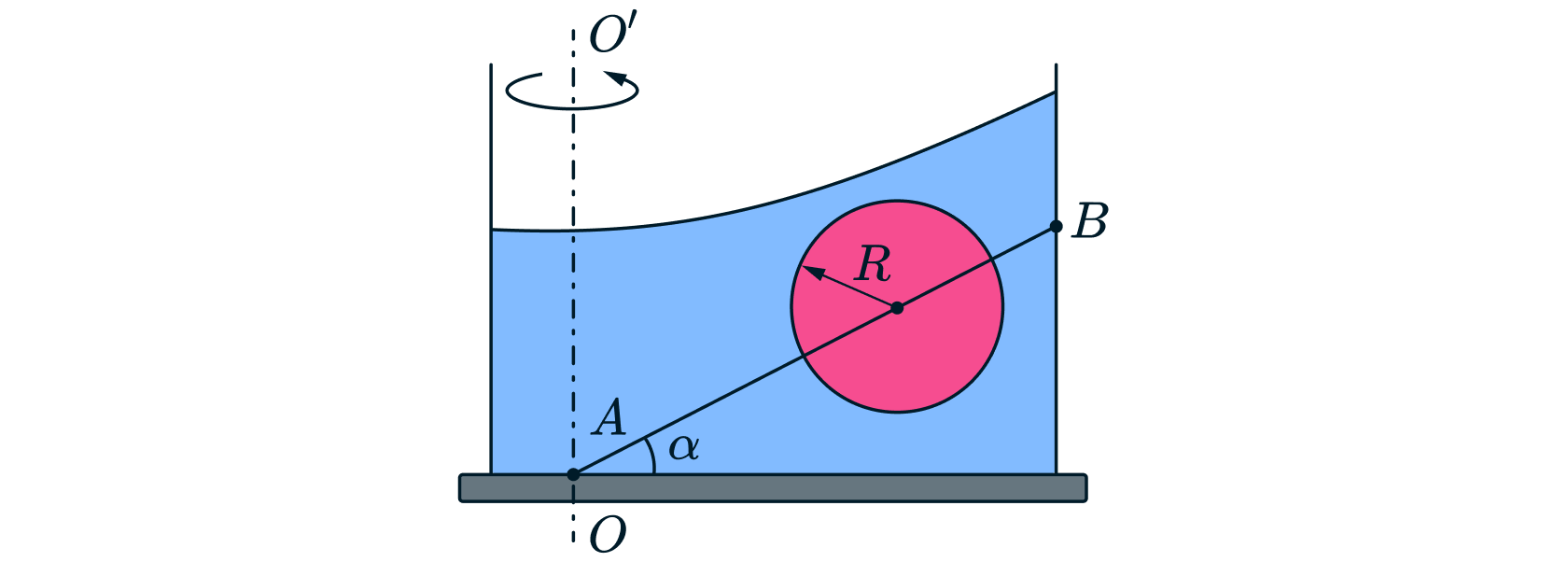
На горизонтальной платформе стоит сосуд с водой. В сосуде закреплён тонкий стержень наклонённый к горизонту
под углом
(рис.). Шар радиусом
может скользить без трения вдоль стержня, проходящего через его центр.
Плотность шара
плотность воды
При вращении системы с постоянной угловой скоростью вокруг
вертикальной оси
проходящей через нижний конец
стержня, центр шара устанавливается на расстоянии
от
этого конца.
1) С какой силой шар действует на стержень?
2) Найдите угловую скорость вращения платформы.
3) При какой минимальной угловой скорости вращения шар «утонет» и окажется на дне сосуда?
Воды достаточно, так что шар всегда полностью погружен в воду.
Источники:
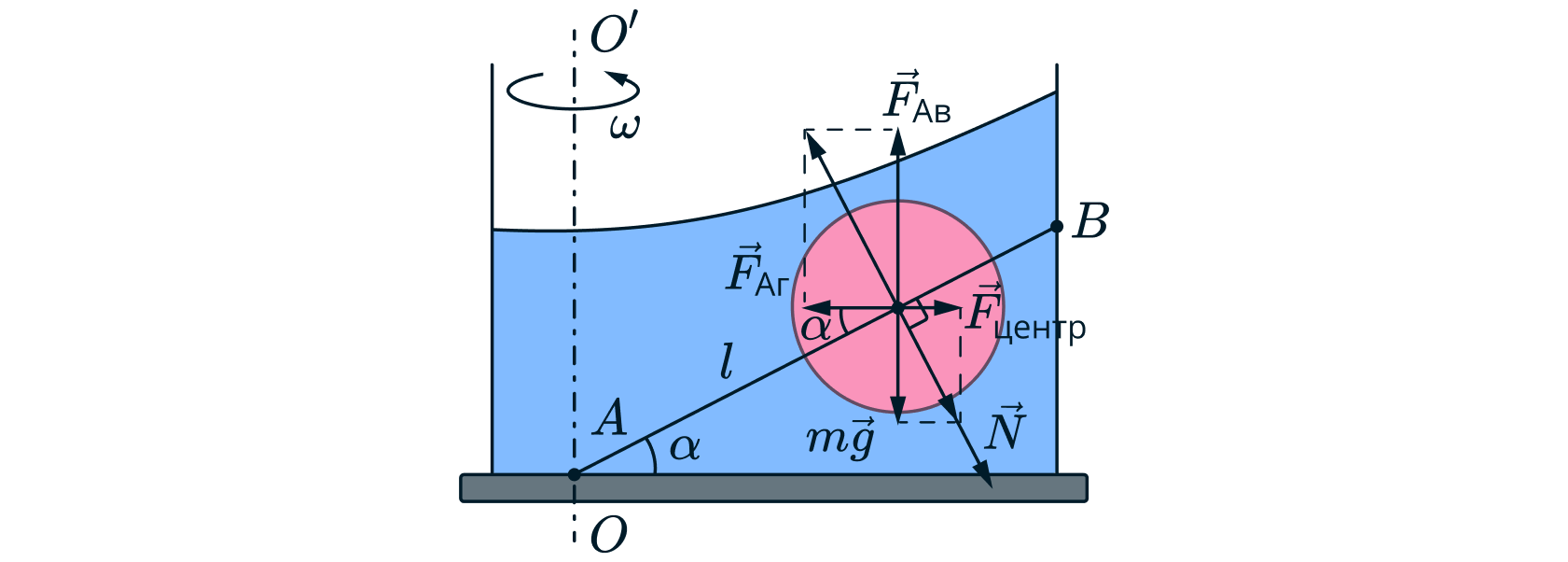
1. Отметим силы, действующие на на шар. Сила Архимеда, действующая на шар по горизонтали вычисляется как
; И, соответственно, Сила Архимеда, действующая на шар по вертикали:
. Так же
на шар в НеИСО действует центробежная сила, направленная вправо
.
Осталось понять, как ориентирована сила реакции опоры. Для этого запишем явно выражения для силы центробежной и силы тяжести.
Теперь несложно заметить следующую вещь:
Отсюда вывод: равнодействующая центробежной силы и силы тяжести лежит на одной прямой с равнодействующей
сил Архимеда и, очевидно, направлена противоположно. Также известно, что шар находится в равновесии, и плотности
тела и жидкости соотносятся как . Отсюда вывод: сила реакции направлена вдоль равнодействующей сил
Архимеда.
2. Пишем условие равновесия в проекции на вертикальную ось:
Ответ на первый вопрос задачи получен.
3. Теперь рассмотрим условие равновесия по горизонтали:
Тогда угловая скорость вычисляется как
4. Теперь рассмотрим ситуацию, когда шар полностью утонул. Для неё снова запишем условие равновесия по горизонтали и получим:
В случае, когда шар полностью утонул . Тогда минимальное значение угловой скорости, при которой шар
утонет и окажется на дне сосуда:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




