17.02 Задачи №17 из сборника И.В. Ященко

а) Если два угла, образованных диагональю и стороной четырехугольника и опирающихся на одну и ту же сторону четырехугольника, равны, то такой четырехугольник является вписанным. Будем пользоваться этим признаком вписанности для доказательства вписанности

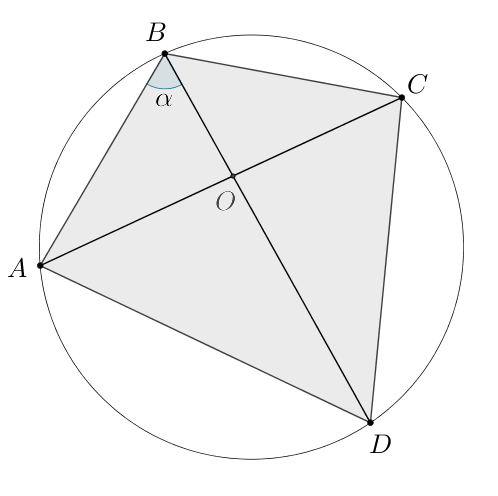
Рассмотрим и Обозначим Заметим, что так как в противном случае а эти углы являются накрест лежащими при секущей

Тогда, так как и подобны, существует два варианта: или В первом случае доказывать больше нечего, четырехугольник является вписанным. Рассмотрим второй случай. Тогда Так как как вертикальные, то следовательно, равнобедренный. Тогда и равнобедренный. Следовательно, Тогда четырехугольник является вписанным. Чтд.

б) Обозначим

1.

Если то при секущей что невозможно.

2.

Пусть Если то при секущей что невозможно.

Пусть Рассмотрим рисунок:

Тогда все углы при вершине опирающиесся на какую-либо сторону четырехугольника, прямые. и — биссектрисы и высоты в и соответственно. Следовательно, эти треугольники равнобедренные. Тогда Заметим также, что следовательно, Следовательно, — высота, опущенная из вершины прямого угла к гипотенузе. Но что невозможно.*

*Высота, опущенная к гипотенузе, ищется по формуле

где — катеты, — гипотенуза.

3.

Пусть Если то при секущей что невозможно. Если то, рассуждая аналогично предыдущему пункту, мы получаем следующую картинку:

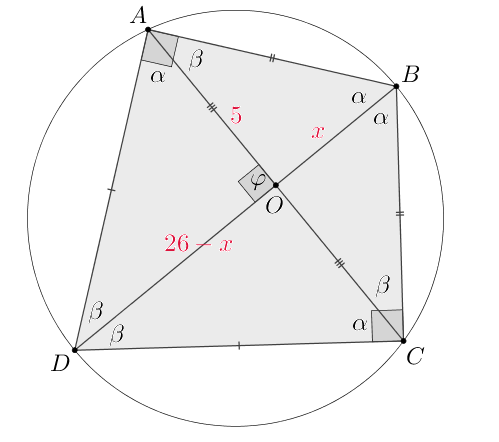
Здесь противоречий нет. Значит это единственно возможный вариант.

Итак, Без ограничения общности пусть Из подобия и получаем

Так как то Тогда по теореме Пифагора

Следовательно. полупериметр четырехугольника равен Площадь же его равна полупроизведению диагоналей, то есть

Тогда радиус вписанной окружности равен