17.02 Задачи №17 из сборника И.В. Ященко
Ошибка.
Попробуйте повторить позже
В четырехугольнике противоположные стороны не параллельны.
Диагонали четырехугольника
пересекаются в точке
под прямым
углом и образуют четыре подобных треугольника, у каждого из которых одна из
вершин — точка
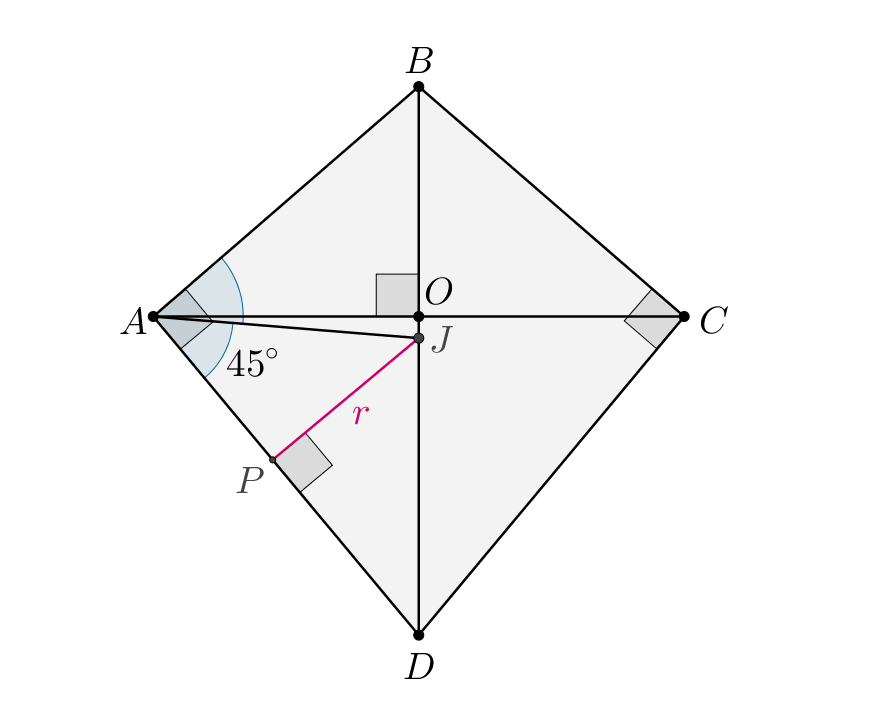
а) Докажите, что в четырехугольник можно вписать окружность.
б) Найдите радиус вписанной окружности, если
Источники:
а) Так как противоположные стороны не параллельны, то
Тогда из подобных по условию треугольников имеем:
Пусть Тогда
что не противоречит
условию на подобие треугольников (два равных треугольника — подобные
треугольники с коэффициентом подобия, равным 1). Следовательно,
—
дельтоид (четырехугольник, диагонали которого взаимно перпендикулярны и одна
из них делит вторую пополам).
Пусть — биссектриса
Тогда биссектрисы углов
и
дельтоида пересекаются в точке
Докажем, что
— биссектриса
Так
как
по трем сторонам, то по свойству биссектрисы
Следовательно, по признаку — биссектриса. Таким образом,
— точка
пересечения биссектрис всех углов четырехугольника
следовательно,
— центр вписанной в него окружности.

Если то аналогично предыдущему случаю
—
дельтоид, но уже с
и
Далее верны аналогичные
рассуждения.
Что и требовалось доказать.
б) Итак, — дельтоид. Из пункта а) следует, что
— вписанный
(
), причем два противоположных угла из четырех равны по
Следовательно, их сумма равна
значит, одна из
диагоналей
или
является диаметром описанной окружности. Докажем,
что это б´ольшая диагональ. Отсюда будет понятно, какие из двух углов дельтоида
прямые.
Предположим, что меньшая диагональ — диаметр описанной окружности.
Тогда
— середина
и центр описанной окружности. Если
делит
пополам, то
следовательно,
Но
так как в этом случае
— ромб, что противоречит условию на
непараллельность противоположных сторон. Если
делит
пополам, то
имеем:
Также противоречие.

Таким образом, — диаметр описанной окружности, следовательно,
Также попутно мы доказали, что именно б´ольшая диагональ
делит меньшую пополам, то есть
— середина
Тогда имеем
Пусть
Тогда получаем систему
Без ограничения общности
1 способ
Воспользуемся формулами и
для площади дельтоида
Тогда
2 способ
По свойству биссектрисы имеем:
Тогда по теореме косинусов из
Заметим, что больше высоты
треугольника
Так как
то нам подходит
Проведем Следовательно, по определению
и есть радиус
вписанной окружности. Из
так как
имеем:
б)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




