.04 Закон Бернулли
Ошибка.
Попробуйте повторить позже
На малых реках иногда устанавливают бесплотинные гидроэлектростанции, которые представляют собой ряд водяных
колес или турбин, опущенных в воду и соединенных с генератором электрического тока. Такая электростанция не
изменяет параметров потока выше по течению, но, безусловно, меняет параметры потока ниже по течению. Определите
максимальную теоретическую мощность электростанции, если русло реки имеет постоянную ширину , постоянную
глубину и прямоугольную форму. Скорость течения реки перед электростанцией равна
, а глубина воды
. Воду
считать несжимаемой жидкостью.
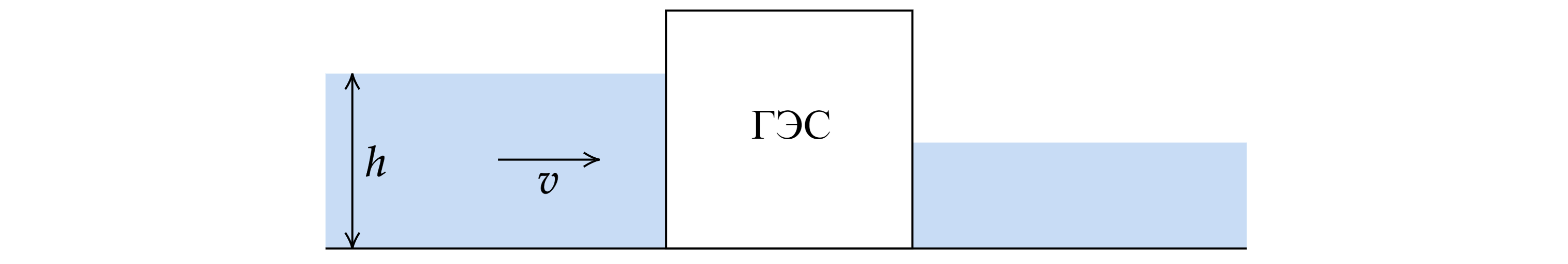
(Надежда Энергетики, 2023, 11)
Источники:
Теоретическая мощность электростанции (в пренебрежении потерь на трение в жидкости, в трансмиссии и не 100%-ом КПД генератора) равна разности потоков энергии в реке выше и ниже по течению. Поток энергии в реке складывается из двух частей. Первая представляет собой просто перенос кинетической и потенциальной энергии воды потоком и равна:
Вторая представляет собой работу сил давления воды в единицу времени:
Итого получаем:
Временно обозначая величины выше по течению индексом 1, а ниже по течению – индексом 2, запишем теоретическую мощность:
При этом, в силу несжимаемости воды, должно выполняться условие равенства потоков выше и ниже по течению:
Таким образом, из двух характеристик потока ниже по течению, и
, только одна является
независимой. Выражая, например,
через
, получаем мощность:
Здесь введено безразмерное отношение:
называемое числом Фруда, равное отношению кинетической и потенциальной энергий воды в верхнем течении. Мощность, как нетрудно убедиться, имеет максимум при:
При этом число Фруда в нижнем течении:
Таким образом:
(Официальное решение Надежда Энергетики)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




