Проецирование в стерео
Ошибка.
Попробуйте повторить позже
Пять рёбер тетраэдра имеют длины и
Определите, может ли при этом длина шестого ребра:
a) равняться
б) равняться
Источники:
Пункт а), подсказка 1
Первое на что хочется в такой задаче обратить внимание — это неравенства треугольника. С них и начнём: две грани имеют общее ребро длиной 2, но можем ли мы составить из имеющихся длин два треугольника, у которых будет сторона 2?
Пункт б), подсказка 1
Много ли у нас вариантов составить треугольники-грани со стороной 2? Выходит что существует всего два треугольника. Будем пробовать построить наш тетраэдр!
Пункт б), подсказка 2
Назовём тетраэдр SABC. Пусть ребро АС = 2. Мы однозначно можем определить и противоположное ему ребро SB. Также, пусть AB = 5, BC = 4. Поработайте с неравенством треугольника для каждой грани, чтобы определить однозначно длины оставшейся пары рёбер.
Пункт б), подсказка 3
На первый взгляд всё сходится, все треугольники-грани существуют, но удастся ли совместить их так, чтобы получился тетраэдр?
Пункт б), подсказка 4
Попробуем оценить длину SC! Для этого построим сначала высоты из вершин S и C в треугольниках △SAB и △CAB соответственно. Затем проведём плоскость перпендикулярную АВ — ребру противоположному SC. Теорема Пифагора поможет нам посчитать длины этих высоты SH и CK, а также определить положение точек Н и К на АВ
Пункт б), подсказка 5
Попробуйте оценить теперь, какую длину может иметь S'C' — проекция ребра SC на проведённую плоскость?) Используйте для этого то, что т.к. проведённые ранее высоты также перпендикулярны AB, их проекции на эту плоскость будут равны самим высотам.
Пункт б), подсказка 6
Итак, получается, что S'C' лежит между |SH - CK| и |SH + CK|. Теорема Пифагора и значение НК помогут нам окончательно, числами, ограничить SC. Вписывается ли известное значение 11.1 в эти ограничения?
(a) У нас есть 2 грани со стороной 2, но вместе с 2 треугольник может образовать только 4 и 5?!
(b) У нас есть 2 грани со стороной 2. Вместе с 2 треугольник может образовать только 4 и 5 или 11,1 и 13. Значит, противоположная
сторона равна 9. Пусть нам дан тетраэдр и
,
,
. Тогда
и по неравенству треугольника для
сторона
. Значит, последняя сторона
.
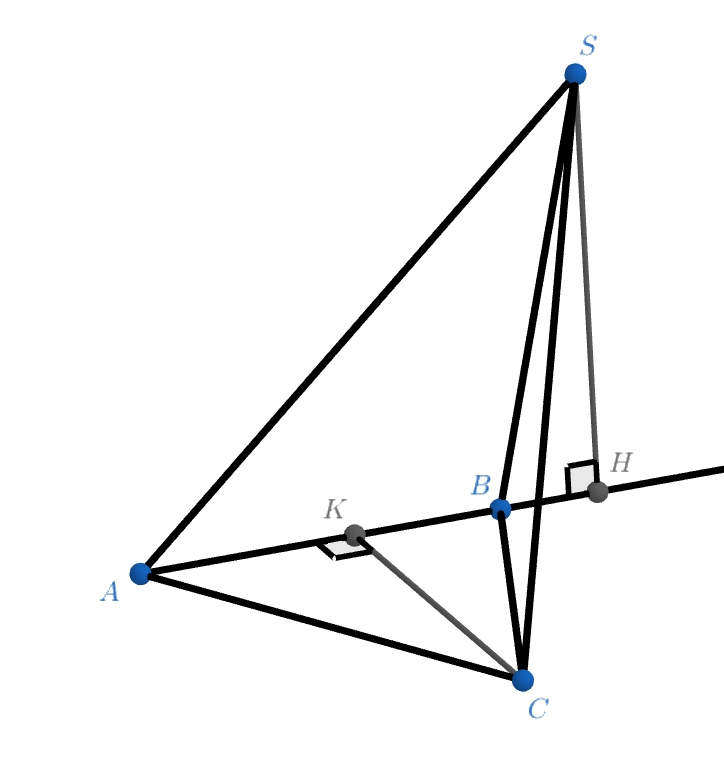
По формуле Герона площадь равна
Тогда если — высота в этом треугольнике, то
. По теореме Пифагора
и
. Отсюда следует, что
лежит на отрезке
Аналогично, , высота
в этом треугольнике длиной
,
,
Значит,
лежит на луче
за точкой
. Отсюда
Вспомним, что у нас есть такое неравенство на
Оно выводится так: спроецируем всё на плоскость, перпендикулярную пусть
— проекция
,
— проекция
,
—
проекция
и
. Так как
и
перпендикулярны
, то
и
Значит, проекция
на эту
плоскость длиной от
до
, а проекция на прямую
это
Значит,
Подставим числа и получится, что так как , а
, то
а) нет
б) нет
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




