Тема Дополнительные построения в стерео

Проецирование в стерео

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дополнительные построения в стерео

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79606

Ортогональной проекцией правильной треугольной пирамиды на некоторую плоскость является параллелограмм с острым углом $60∘$ . Найдите объём пирамиды, если площадь её боковой поверхности равна 54.

Источники: ОММО - 2024, задача 8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Чтобы нормально работать с картинкой, рассмотрим две пары скрещивающихся рёбер пирамиды (например, AB, CD, BC, AD). Ведь их достаточно для построения проекции. Пирамида правильная, значит, на этих рёбрах удобно отметить их середины (например, точки M, N, Q, P соответственно). Ведь отрезки MN и PQ являются перпендикулярами к этим рёбрам. Но, кажется, этого мало, ведь надо понять, какие свойства имеют их проекции. Попробуйте выяснить, как связаны эти отрезки и их проекции, основываясь на том, что ортогональная проекция пирамиды - параллелограмм.

Подсказка 2

В силу того, что проекцией пирамиды является параллелограмм, эти отрезки параллельны плоскости проекции. Тогда проекции MN и PQ параллельны самим отрезкам, равны им и перпендикулярны сторонам ромба. Также, так как пирамида правильная, MN и PQ равны, а значит, и их проекции тоже. Что тогда мы можем сказать про этот параллелограмм?

Подсказка 3

Верно! Это же ромб! Ведь в нём высоты, проведённые к смежным сторонам, равны. Тогда, если введём угол между ребром основания пирамиды и плоскостью проекции и длину стороны основания и боковой стороны трапеции (например, через a и b), то сможем выразить стороны ромба через a, b и этот угол и получить уравнение, ведь эти стороны равны.

Подсказка 4

Теперь мы получили, что тангенс угла между ребром основания пирамиды и плоскостью проекции равен a/b. Отлично! Мы можем выразить и синус, и косинус этого угла через a/b, а значит, и сторону ромба мы можем выразить через a и b (для удобства можно заменить a/b на новую переменную). Но мы ещё никак не воспользовались тем условием, что угол ромба равен 60 градусам. Это нужно исправить, например, записав уравнение на синус этого угла, выразив его как отношение высоты ромба на его сторону. Если мы ещё и выразим высоту через a и b, то получится записать уравнение на a и b.

Подсказка 5

Мы ведь знаем, что проекция MN - это высота ромба. Тогда так как проекция равна MN, то и высота равна этому отрезку. А вот его уже легче искать. Это можно сделать, выразив площадь треугольника MDC двумя способами.

Подсказка 6

Подставив MN в уравнение, мы получили, что (a/b)^2 = 2. Осталось воспользоваться последним условием задачи про площадь боковой поверхности. Выразив её через a и b, мы получаем уравнение, через которое находим a и b. Дело за малым, осталось лишь посчитать объём. И победа!

Показать ответ и решение

Пусть сторона основания пирамиды $DABC$ с вершиной $D$ равна $a$ , а боковое ребро равно $b$ . Для построения проекции достаточно рассмотреть две пары скрещивающихся ребер, например, $AB, CD,BC$ и $AD$ , проекции которых являются сторонами параллелограмма $A1B1C1D1.$

$PIC$

Пусть $MN$ — общий перпендикуляр пары рёбер $AB$ и $CD$ , а $PQ$ — общий перпендикуляр скрещивающихся рёбер $AD$ и $BC.$ Плоскость проекции $Ω$ параллельна как $MN$ , так и $P Q$ , поскольку ортогональной проекцией пирамиды является параллелограмм. Отрезки $MN$ и $PQ$ проектируются на плоскость $Ω$ без изменения длины в высоты параллелограмма $M1N1$ и $P1Q1$ , так как $ABB1A1$ и $DCC1D1$ обе перпендикулярны $Ω$ и будут параллельны друг другу, т.к. $A1B1C1D1$ — параллелограмм. То есть $MN$ не просто общий перпендикуляр $AB$ и $CD$ , но и общий перпендикуляр двух вышеописанных плоскостей. А значит, ещё это и общий перпендикуляр для $A1B1$ и $C1D1.$

Поскольку пирамида правильная, $MN = PQ$ . Следовательно, $M1N1 = P1Q1.$

В параллелограмме $A1B1C1D1$ высоты, проведённые к смежным сторонам, равны. Значит, параллелограмм является ромбом.

Пусть ребро $AB$ наклонено к плоскости $Ω$ под углом $α$ , тогда ребро $CD$ , которое перпендикулярно $AB$ , наклонено под углом $90∘− α.$ Отсюда $acosα= bsinα.$

$PIC$

Обозначим $ab = λ$ . Тогда $tgα= λ,A1B1 = acosα = √1a+λ2$ .

Найдём расстояние между скрещивающимися рёбрами правильной треугольной пирамиды как высоту сечения $DMC$ :

∘ ------ a√3- 2 a2 MC ⋅H = b⋅MN, 2 ⋅ b − 3 = b⋅MN

откуда

∘------ ∘----- MN = a2b 3b2− a2 = a2 3− λ2

Тогда синус острого угла пирамиды равен $sinφ = MA11ND11 = AM1NB1$ . Подставляя найденные выражения и данное в условии значение $φ =60∘$ , получим $- √32 = 12√3-−-λ2√1-+λ2-$ , откуда $λ= 0$ (что невозможно) или $λ2 =2.$

Площадь боковой поверхности пирамиды равна

∘ ----2- 2 √----2 S = 3a b2− a-= 3a-⋅-4−-λ- 2 4 4 λ

Подставив $S = 54$ и $λ= √2$ , найдём

a2 =72,b2 = a2= 36 λ2

Объём правильной пирамиды равен

a2∘ --2--2 √------- V = 12 3b − a = 6 108− 72=36

Ответ: 36

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68182

На плоскости в ортогональной проекции изображена правильная пирамида $SABC$ (с основанием $ABC$ ) и высота $AH$ грани $SAB,$ как показано на рисунке.

$PIC$

Как с помощью циркуля и линейки построить изображение центра сферы, описанной возле пирамиды?

Источники: ФЕ-2023, 11.4 (см. www.formulo.org)

Подсказки к задаче

Подсказка 1

Для начала подумаем, вообще где должен быть центр сферы. Ну он лежит точно в плоскости, которая перпендикулярна ребру... А через какую точку на ребре будет проходить такая плоскость?

Подсказка 2

В нашем случае - через середину, а середину ребра мы точно сможем сделать) Теперь подумаем где еще может быть центр описанной окружности в правильной пирамиде. Например, на высоте) А эту высоту как раз можно найти в нашей плоскости. Но надо еще понять как построить само основание высоты...

Подсказка 3

В нашем случае, основание высоты будет также центром основания и пересечением медиан, которое мы точно умеем строить: просто пересекая медианы. Осталось найти еще бы одну прямую, что если пересечь ее с высотой, то получится нужная точка....

Подсказка 4

Напомню, что прямая AH перпендикулярна ребру SB, а у нас еще есть середина стороны...

Показать ответ и решение

$PIC$

Пусть $M$ - середина $AC,$ $N$ - центр основания $ABC.$ Тогда центр описанной сферы лежит на $SN$ (поскольку пирамида правильная). Проекция $M$ строится как середина проекции $AC,$ а проекция $N$ – как точка, делящая проекцию $BM$ в отношении $2:1.$ Обозначим через $m$ прямую, параллельную $MH$ и проходящую через середину $SB.$ Она проходит через центр описанной сферы: $AH$ и $CH$ перпендикулярны $SB,$ так что $m$ перпендикулярна $SB,$ а также $m$ пересекает $SN.$ Проекция $m$ строится как параллельный перенос проекции $MH,$ проходящий через середину проекции $SB.$ Эта проекция пересекает проекцию $SN$ ровно в проекции центра описанной сферы.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 3#68261

Дано несколько прямоугольных параллелепипедов в пространстве. Известно, что у каждой пары параллелепипедов есть хотя бы одна общая точка, а их рёбра соответственно параллельны. Обязательно ли все параллелепипеды имеют общую точку?

Источники: БИБН-2023, 11.4 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Если попытаться построить пример, то не особо получится, что у них у всех нет общей точки...Стоит попробовать доказать, что она всегда есть! Что можно сделать для этого?

Подсказка 2

При построении примера, скорее всего, были ещё трудности: в пространстве сложно нормально нарисовать картинку....Так, давайте спроецируем всё, например, на одну из координатных осей, т.к. это параллелепипеды и у них соответствующие ребра параллельны) Как теперь будет выглядеть условие?

Подсказка 3

Теперь у нас на прямой есть отрезки вида [ai, bi], и каждые два из них пересекаются. Чтобы доказать, что у них всех есть общая точка, посмотрите на конфигурацию, где вы понимаете, что у них у всех есть непустое пересечение)

Подсказка 4

Ну и осталось просто сказать это для всех трех координатных осей. Задача решена!

Показать ответ и решение

Поскольку у параллелепипедов ребра соответственно параллельны, мы можем ввести декартову систему координат, направив оси вдоль трех ребер, смежных с одной вершиной (которая станет началом координат) выбранного параллелепипеда. В этой системе координат ребра всех параллелепипедов будут параллельны осям. Спроектировав на ось Ох данный $i$ -ый параллелепипед $(i= 1,2,...,n),$ получим отрезок, который обозначим $[ai,bi].$ Любая пара таких отрезков имеет непустое пересечение (в противном случае соответствующая пара параллелепипедов не пересекается).

Таким образом, приходим к такой задаче: на числовой прямой есть попарно пересекающиеся отрезки $[ai,bi],(i=1,2,...,n),$ и требуется доказать, что у них имеется общая точка. Опытные олимпиадники могут сразу сослаться на теорему Хелли. Мы же приведём её доказательство, чтобы не оставлять у неопытных читателей чувство неловкости.

Пусть $A$ – наибольшее значение среди левых концов отрезков, т.е. $A= max{ai|i=1,...n},$ и аналогично, пусть $B$ — наименьшее значение среди правых концов отрезков. Тогда $A ≤B,$ так как в противном случае $ai > bj$ для некоторых $i$ и $j,$ а значит, $i$ -ый и $j$ -ый отрезки не пересекаются. Отсюда следует, что любая точка отрезка $[A,B]$ будет общей для всех наших отрезков. Итак, пусть точка $x∗$ принадлежит проекциям на ось Ох всех параллелепипедов. Точно так же мы можем найти общие точки $y∗$ и $z∗$ проекций на оси Oy и Oz. Тогда точка с координатами $(x∗,y∗,z∗)$ будет принадлежать всем параллелепипедам.

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 4#76531

$A′,$ $B′$ и $C′$ — проекции вершины $S$ правильной треугольной пирамиды $SABC$ на биссекторные плоскости двугранных углов при рёбрах $BC,$ $AC$ и $AB.$ Найдите тангенс каждого из этих углов, если объём пирамиды $′ ′ ′ SA BC$ в $10$ раз меньше объёма пирамиды $SABC.$

Источники: Миссия выполнима - 2022, 11.4 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Сходу непонятно, что делать с условием на перпендикуляры к плоскостям, может, попытаться сделать какое-то дополнительное построение, связанное с вершиной S и одной из этих плоскостей?

Подсказка 2

Правильно, сделать симметрию точки S относительно плоскости A'BC и получить точку S₁. Попробуйте получить точки S₂, S₃ по такой же симметрии, только относительно AB'C и ABC'.

Подсказка 3

Мы получили треугольник S₁S₂S₃, кажется, что он концентричен с треугольником ABC (докажите это, используя поворот относительно высоты пирамиды).

Подсказка 4

Треугольник PSS₁ равнобедренный (P - середина BC), так как PA' - высота и биссектриса, а значит SA'=A'S₁, следовательно, пирамида SS₁S₂S₃ является образом SA'B'C' при гомотетии с коэффициентом 2 и центром в S, а значит, как относятся их объемы?

Подсказка 5

Правильно, в 8 раз. Теперь мы можем использовать условие с отношениями объемов SABC и SA'B'C', найдя отношение объемов SABC и SS₁S₂S₃ и отношение площадей их оснований.

Подсказка 6

Проведём высоту SO нашей пирамиды и найдем отношение S₁O/AO с помощью отношения площадей.

Подсказка 7

Выразим S₁O и OA через SO и найдем тангенс угла, который нужно вычислить в задаче с помощью найденных отрезков.

Показать ответ и решение

Точки $S ,S , 1 2$ и $S 3$ симметричные $S$ относительно биссекторных плоскостей, лежат в плоскости $ABC.$ А поскольку тройка этих биссекторных плоскостей переходит в себя при повороте на $∘ 60$ вокруг оси пирамиды, то этим свойством обладает и тройка точек $S1,S2,S3.$ Следовательно, треугольник $△S1S2S3$ — правильный, и его центр, который мы обозначим через $O,$ совпадает с центром треугольника $△ABC.$

$PIC$

Заметим, далее, что пирамида $SS1S2S3$ —- образ пирамиды $SA′B ′C ′$ при гомотетии с центром $S$ и коэффициентом $2.$ С учётом условия задачи это означает, что отношение объёмов пирамид $SABC$ и $SS1S2S3$ равно $10:23 =5 :4.$ А поскольку у этих пирамид общая высота $SO,$ то и отношение площади треугольника $△ABC$ к площади треугольника $△S1S2S3$ равно $5:4.$ В качестве следствия получается равенство $OA :OS1 = √5 :2,$ которое будет нами использовано.

Обозначив величину двугранного ребра при ребре $BC$ через $φ$ , точкой, симметричной $S$ относительно соответствующей биссекторной плоскости будем считать $S1.$

$PIC$

Тогда $φ= ∠SPA = ∠SPS1,$ где $P$ — середина ребра $BC$ ; треугольник $△SP S1$ — равнобедренный $(SP = PS1),$ откуда

180∘ − φ φ ∠SS1P = ---2--,OS1 =SO ctg∠SS1P = SOtg2-

А поскольку

OA = 2⋅AP = 2⋅SOctg φ, 2

то

√5 OA 2ctgφ -2-= OS1 =-tg φ2

tg φtgφ = 4√- 2 5

При $0∘ < φ< 90∘$ левая часть последнего равенства равна $∘1+-tg2φ− 1,$ что позволяет найти

∘16+-8√5- tgφ = ---5---

Ответ:

$∘ 16+-8√5 ---5---$

Ошибка.
Попробуйте повторить позже

Задача 5#92143

Вася смастерил из стеклянных стержней призму. Призма имеет 171 боковое ребро и столько же рёбер в каждом из оснований. Вася задумался: «Можно ли параллелыо перенести каждое из 513 рёбер призмы так, чтобы они образовали замкнутую ломаную в пространстве?»

Возможна ли реализация Васиной задумки?

Источники: ОММО - 2021, номер 10 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Если у нас произвольное количество вершин, то мы там будем в смысле прохождения через боковые ребра(при наличии искомой ломаной), будем то подниматься на высоту равную длине бокового ребра, то опускаться. И при этом, у нас замкнутая ломаная, то есть мы вернулись в начальную точку. Как формализовать эти «прыжки»?

Подсказка 2

Формализовать очень просто - давайте введем такую систему координат, что плоскость Oxy параллельна основанию, а Oz перпендикулярна ему же. Тогда мы получаем, что если у нас такая ломаная вышла, то мы только при прохождении через боковые ребра меняем высоту. При этом суммарно смен 171 и ломаная замкнутая. Что из этого следует и какой тогда ответ?

Показать ответ и решение

Предположим, что реализация Васиной задумки возможна, и рассмотрим замкнутую ломаную, образованную 513 рёбрами. Введём систему координат таким образом, что плоскость $Oxy$ была параллельна основаниям призмы, ось $Oz$ перпендикулярна основаниям призмы, причём высота призмы равнялась 1 , а начало координат $O$ совпадало с одной из вершин замкнутой ломаной.

Пойдём теперь по нашей ломаной, начиная с точки $O$ . Каждый раз, когда мы переходим по ребру, которое лежало в основании, мы движемся в плоскости, параллельной $Oxy$ , т.е. $z$ -координата вершишы ломаной не меняется. Если же мы проходим по ребру, которое было боковым ребром, мы меняем $z$ -координату ровно на 1 .

Таким образом, когда мы пройдём по всем 513 рёбрам и вернёмся в точку $O$ , $z$ -координата вершишы, с одной стороны, должна стать 0 , с другой сторюны, она должна быть нечётной, т.к. мы 171 раз поменяли её чётность. Противоречие.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 6#63889

Дан тетраэдр $ABCD$ . Известно, что $AB = BC =CD = 5$ и $CA = AD =DB = 6$ . Найдите косинус угла между рёбрами $BC$ и $AD.$

Источники: ДВИ - 2020, вариант 202, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Какие способы поиска угла между скрещивающимися прямыми нам в принципе известны? В первую очередь хочется подумать о проведении прямой параллельной одной из них через точку на второй прямой. Будем рассматривать плоскость, проходящую через BC параллельно AD.

Подсказка 2

Чтобы построить искомый угол, ортогонально спроецируем точку А на построенную плоскость. Пусть получена точка А'. Рассмотрим отрезок MN, где N — cередина AD, M — середина ВС. Данных нам равенств отрезков достаточно, чтобы доказать, что он является общим перпендикуляром прямых AD и BC. Тогда какой угол будет искомым?)

Подсказка 3

Искомый угол ∠A'MB. Знание об общем перпендикуляре сразу же помогает нам найти А'М. Но чего-то ещё не хватает... Попробуем построить тут прямоугольный треугольник, чтобы легче было выражать угол! АА' перпендикуляр. Проведём из точки А наклонную АН такую что, точка Н лежит на ВС и АН ⊥ ВС. Тогда теорема о трёх перпендикулярах поможет нам увидеть △А'НМ с прямым углом Н, известной гипотенузой А'М и острым углом, чей косинус так хочется узнать!

Подсказка 4

Наклонная АН будет по сути высотой в треугольнике △АВС. При всех известных сторонах нетрудной найти АН и ВН. Отсюда один шаг до катета МН. Подставьте все нужные длины и получите косинус искомого угла!

Показать ответ и решение

Рассмотрим треугольник $ABC$ . Высота, опущенная из вершины $B$ , равна 4 , следовательно, высота $AH$ , опущенная из вершины $A$ , равна 24/5. Отсюда получаем $18 7 CH = 5 ,BH = 5$ . Пусть $M$ — середина $BC$ . Тогда $5 7 11 MH = 2 − 5 = 10.$

$PIC$

Пусть $N$ — середина $AD$ . Тогда $BN = CN$ и, стало быть, $MN ⊥ BC$ . Аналогично $MN ⊥$ $AD$ .

Рассмотрим плоскость, содержащую $BC$ и параллельную $AD$ . Спроецируем ортогонально на эту плоскость точки $A$ и $D$ . Полученные точки обозначим $A′$ и $D′$ . Точка $N$ при этом проецируется в точку $M$ . Стало быть, искомый угол равен $∠A ′MB$ .

Из прямоугольного треугольника $A′MH$ получаем

cos∠A′MB = cos∠A′MH = MH--= MH--= 11. A′M AD∕2 30

Ответ:

$11 30$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#43959

Дана усечённая пирамида $ABCA B C 1 1 1$ с боковыми рёбрами $AA 1$ , $BB 1$ , $CC 1$ $(ABC ∥A B C ) 1 1 1$ , такая, что треугольник $BB1C$ — равносторонний. На ребре $AA1$ , перпендикулярном основанию $ABC$ пирамиды, лежит точка $N$ такая, что $AN :NA1 = 1:2.$ Сфера $Ω$ с радиусом $√- 5$ проходит через вершины треугольника $BB1C$ и касается отрезка $AA1$ в точке $N$ .

(a) Найдите длину ребра $BB1$ .

(b) Пусть дополнительно известно, что $∘ -- ∠ABC =arccos 25$ . Найдите угол между прямой $AA1$ и плоскостью $BB1C$ , а также длину ребра $A1B1.$

Подсказки к задаче

Пункт а), подсказка 1

Введем обозначения: пусть E – вершина пирамиды, O – центр сферы ω, O₁ – центр описанной окружности треугольника BB₁C, а F – середина BC. Если треугольник BB₁C равносторонний, то чем еще будет являться точка O₁? А какие прямые будут проходить через нее?

Пункт а), подсказка 2

Верно, O₁ будет также точкой пересечения медиан, значит через нее пройдет прямая B₁F, Вы даже можете спокойно найти, в каком отношении точка O₁ поделит отрезок B₁F. А что тогда можно будет сказать про взаимное расположение прямой NO₁ и плоскости (ABC)?

Пункт а), подсказка 3

Конечно, прямая NO₁ будет параллельна плоскости (ABC). А теперь поработаем с нашей сферой! Из условия сфера касается AA₁ в точке N, а также проходит через вершины треугольника BB₁C, чему тогда будут перпендикулярны прямые OO₁ и ON?

Пункт а), подсказка 4

OO₁ ⊥ (BB₁C), ON ⊥ AA₁, а еще по условию AA₁ ⊥ (ABC), тогда ON будет параллельна плоскости (ABC)! Остается понять, что точка O₁ совпадает с точкой O. Для этого рассмотрите плоскость α, которая будет проходить через точку N параллельно плоскости (ABC), а также рассмотрите прямую l, которая перпендикулярна (BB₁C) и проходит через точку O₁. Что будет, если прямая l будет лежать в плоскости α?

Пункт а), подсказка 5

Действительно, такой ситуации быть не может, ведь тогда FB₁ ⊥ l, FB₁ ⊥ BC, а это две разные прямые, которые параллельны (ABC), тогда получается, что (BB₁C) ⊥ (ABC), а такого не может быть в нашей пирамиде! Тогда делаем вывод, что l пересекает α в одной точке, поэтому O₁ = O, что и хотелось показать. Теперь вовсе не составит труда найти сторону равностороннего треугольника BB₁C, если известно, что радиус его описанной окружности совпадает с радиусом сферы.

Пункт б), подсказка 1

Пусть O' – проекция O на (ABC), а B₁' – проекция B₁ на (ABC). Какой прямой в плоскости (ABC) будет принадлежать точка B₁'?

Пункт б), подсказка 2

Конечно, B₁' ∈ AB, можем даже узнать, в каком отношении точка O' будет делить отрезок FB₁' (покажите, что оно будет равно FO : OB₁). Тогда теперь можно будет найти длину отрезка B₁'F, нужно всего лишь показать, что треугольник BB₁'C равнобедренный, доказав равенство треугольников B₁B₁'B и B₁B₁'C. И нужный угол легко найдется, если рассмотреть угол между B₁B₁' || A₁A и нужной плоскостью.

Пункт б), подсказка 3

Пусть T – проекция O' на AB. Легко понять, что A₁B₁ = AB₁', тогда задача поиска A₁B₁ сведется к тому, что нужно будет найти AB₁' = AT + TB₁'. Найдите длину O’T, поработав с треугольником BB₁'C, а зная O’T, можно будет легко найти AT и TB₁', используя теорему Пифагора, а также факт, что AO' = ON.

Показать ответ и решение

$PIC$

Отметим точку $E$ в качестве вершины пирамиды, точку $O$ в качестве центра $ω$ , точку $O1$ в качестве центра описанной окружности треугольника $BB1C$ и $F$ в качестве середины $BC$ . Так как $BB1C$ равносторонний, то $O1$ это еще и центр пересечения медиан, а значит, $B1F$ проходит через $O1$ и $FO1 :O1B1 = 1:2$ и $NO1∥ABC$ . Так как $ω$ проходит через вершины треугольника $BB1C$ и касается отрезка $AA1$ в точке $N$ , то $OO1⊥BCC1$ и $ON ⊥AA1$ . Мы знаем, что $AA1 ⊥ABC$ и поэтому $NO ∥ABC$ . Получается, что мы знаем, что точка $O$ лежит на плоскости $α$ , проходящей через $N$ и параллельной $ABC$ , и лежит на прямой $l$ , перпендикулярной $BB1C$ и проходящей через $O1$ . Значит, либо $l$ принадлежит $α$ , но тогда $FB1$ перпендикулярна двум разным прямым параллельным $ABC$ ( $BC$ и $l$ ) и тогда все три стороны перпендикулярны основанию, а такого не бывает, либо $l$ и $α$ пересекаются в одной точке и $O1 =O$ . Тогда $BO =BO1 = √5$ и $BB1 = √15$ (по формуле для равностороннего треугольника).

$PIC$

Спроецируем точки $O$ и $B1$ на плоскость $ABC$ . Тогда так как проекция $A1$ на $ABC$ это $A$ , то $′ A1B1∥AB 1$ и поэтому $′ B ∈ AB$ . Также можно заметить $′ ′ ′ F O:OB1 = FO :O B1 = 1:2$ .

Прямоугольные треугольники $B1B′1B$ и $B1B′1C$ равны по катету и гипотенузе, поэтому $BB′1 =CB ′1$ . Значит, высота в равнобедренном треугольнике $BB ′1C$ равна $B ′1F$ , так как $F$ середина $BC$ и равна $√--∘-- ∘-- BF |tgB ′1BF |= -125 32 = 458$ . Тогда

∘-- ′ ′ (B′1F-) -458- 1-- ∠(AA1,BCB1)= ∠(B1B1,BCB1 )= ∠B1B1F =arcsin B1F = arcsin √45 = √2 2

Значит, $∠(AA1,BCB1 )= π4$ . Тогда $∘ -- FB ′1 = F√B21= 485$

Пусть $T$ — проекция $O′$ на $AB$ . Тогда $O′T = O′B′cosB ′O ′T = 2B′Fcos1∠B ′O′C = 2B′FcosB ′BC = 2∘ 45∘-2= 1 1 1 3 1 2 1 3 1 1 3 8 5$ и $∘----------- ∘ 3- B1′T = O′B′12− O ′T2 = 2$ . С другой стороны, поскольку $√- AO ′= NO = 5$ , то $√---------- AT = AO ′2− O′T2 = 1$ . Отсюда $∘ -- A1B1 =AB ′1 = AT +TB ′1 = 2+ 32$ .

Ответ:

$(a)√15,$

$π ∘-3 (b)4,2+ 2$

Ошибка.
Попробуйте повторить позже

Задача 8#47912

Существует ли $9$ -угольная пирамида, на ребрах которой можно выбрать направления (стрелки) так, чтобы сумма всех $18$ векторов-ребер равнялась нулевому вектору?

Подсказки к задаче

Подсказка 1

Кажется, что работать с векторами в пространстве — затея не самая приятная... Хотелось бы как-то перенестись в пространство меньшей размерности, может быть, на какую-нибудь прямую, где уже будет легче работать! Можно ли это сделать?

Подсказка 2

Естественно, ведь векторы можно проецировать! Тогда можно выбрать «хорошую» прямую, на которую будет удобно проецировать... Высота пирамиды здорово подойдёт! Что же станет с суммой векторов после проецирования?

Подсказка 3

Останется только сумма равных по модулю проекций девяти ненулевых векторов, которые являются боковыми рёбрами. Раз сумма векторов должна быть равна нулевому вектору, то и сумма их проекций должна быть равна нулю. Возможно ли такое, учитывая предыдущие наблюдения?

Подсказка 4

Эти девять проекций, конечно, равны по модулю, но могут иметь разные знаки. И их сумма равна нулю... Осталось сделать выводы про количества положительных и отрицательных проекций!

Показать ответ и решение

Рассмотрим систему координат с центром в основании высоты пирамиды, одну из осей направим вдоль самой высоты. Тогда длина проекции на эту ось, то есть соответствующая координата, каждого вектора будет равна нулю для рёбер из основания и иметь одинаковое по модулю значение для боковых рёбер — длина высоты с положительным или отрицательным знаком.

Чтобы сумма векторов была нулевой необходимо, чтобы сумма этих координат (соответствующая координата суммы) была равна нулю.

Пусть длина высоты равна $h$ и $n$ координат из $9$ ненулевых положительны, тогда эта координата равна

h⋅n− h⋅(9− n)= h⋅(2n− 9)⁄=0

Но поскольку $2n− 9⁄= 0,n∈ ℕ$ по чётности, а также $h> 0$ из условия, значит, нулевой сумма векторов-рёбер быть не может.

Ответ:

нет

Ошибка.
Попробуйте повторить позже

Задача 9#64564

Пять рёбер тетраэдра имеют длины $2,4,5,9$ и $13.$ Определите, может ли при этом длина шестого ребра:

a) равняться $11;$

б) равняться $11,1.$

Источники: ПВГ-2013, 11.5 (см. pvg.mk.ru)

Подсказки к задаче

Пункт а), подсказка 1

Первое на что хочется в такой задаче обратить внимание — это неравенства треугольника. С них и начнём: две грани имеют общее ребро длиной 2, но можем ли мы составить из имеющихся длин два треугольника, у которых будет сторона 2?

Пункт б), подсказка 1

Много ли у нас вариантов составить треугольники-грани со стороной 2? Выходит что существует всего два треугольника. Будем пробовать построить наш тетраэдр!

Пункт б), подсказка 2

Назовём тетраэдр SABC. Пусть ребро АС = 2. Мы однозначно можем определить и противоположное ему ребро SB. Также, пусть AB = 5, BC = 4. Поработайте с неравенством треугольника для каждой грани, чтобы определить однозначно длины оставшейся пары рёбер.

Пункт б), подсказка 3

На первый взгляд всё сходится, все треугольники-грани существуют, но удастся ли совместить их так, чтобы получился тетраэдр?

Пункт б), подсказка 4

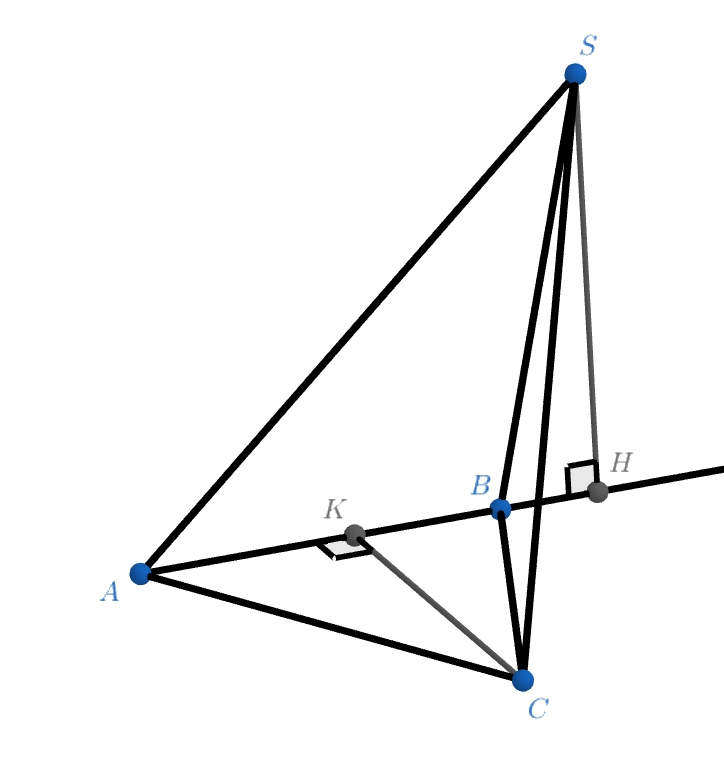
Попробуем оценить длину SC! Для этого построим сначала высоты из вершин S и C в треугольниках △SAB и △CAB соответственно. Затем проведём плоскость перпендикулярную АВ — ребру противоположному SC. Теорема Пифагора поможет нам посчитать длины этих высоты SH и CK, а также определить положение точек Н и К на АВ

Пункт б), подсказка 5

Попробуйте оценить теперь, какую длину может иметь S'C' — проекция ребра SC на проведённую плоскость?) Используйте для этого то, что т.к. проведённые ранее высоты также перпендикулярны AB, их проекции на эту плоскость будут равны самим высотам.

Пункт б), подсказка 6

Итак, получается, что S'C' лежит между |SH - CK| и |SH + CK|. Теорема Пифагора и значение НК помогут нам окончательно, числами, ограничить SC. Вписывается ли известное значение 11.1 в эти ограничения?

Показать ответ и решение

(a) У нас есть 2 грани со стороной 2, но вместе с 2 треугольник может образовать только 4 и 5?!

(b) У нас есть 2 грани со стороной 2. Вместе с 2 треугольник может образовать только 4 и 5 или 11,1 и 13. Значит, противоположная сторона равна 9. Пусть нам дан тетраэдр $SABC$ и $AC = 2$ , $AB =5$ , $BC = 4$ . Тогда $SB =9$ и по неравенству треугольника для $CBS$ сторона $SC = 11.1$ . Значит, последняя сторона $SA= 13$ .

$PIC$

По формуле Герона площадь $ABC$ равна

∘ 11-7--1-3- 1√--- 2-⋅2 ⋅2 ⋅2 = 4 231.

Тогда если $CK$ — высота в этом треугольнике, то $√--- CK = -21310-$ . По теореме Пифагора $√ --------- AK = AC2− CK2 = 1.3$ и $√ --------- BK = BC2− CK2 = 3.7$ . Отсюда следует, что $K$ лежит на отрезке $AB$

Аналогично, $√-- SABS = 94 51$ , высота $SH$ в этом треугольнике длиной $√-- 190 51$ , $BH = 6,3$ , $AH = 11,3.$ Значит, $H$ лежит на луче $AB$ за точкой $B$ . Отсюда $HK = HB + BK =10.$