Стереометрия на ДВИ
Ошибка.
Попробуйте повторить позже
Дан куб с основаниями
и боковыми ребрами
Длина ребра этого куба равна 1. На диагонали
основания
отмечена точка
так, что
Найдите площадь сечения данного куба, проходящего через его центр
и перпендикулярного прямой
Источники:
Подсказка 1
Как нам построить желаемое сечение? Может, оно должно содержать какую-то прямую?
Подсказка 2
Рассмотрите плоскость ACC'.
Подсказка 3
Проведите в ней прямую, перпендикулярную OE, пусть точки T и K являются точками пересечения этой прямой с отрезками AC и A'C' соответственно. Можно ли найти еще одну прямую, перпендикулярную OE?
Подсказка 4
Рассмотрите проекцию OE на плоскость ABC. Попробуйте увидеть теорему о трех перпендикулярах.
Подсказка 5
Как теперь построить сечение? Может, надо провести какие-то параллельные прямые?
Подсказка 6
Например, можно провести через точку O прямую, параллельную BD.
Подсказка 7
А как удобнее было бы искать площадь сечения?
Подсказка 8
Можно ведь ее выразить через площадь проекции на некоторую плоскость и косинус угла!
Проведём прямую в плоскости перпендикулярно
пусть точки
и
являются точками пересечения этой прямой с
отрезками
и
соответственно.
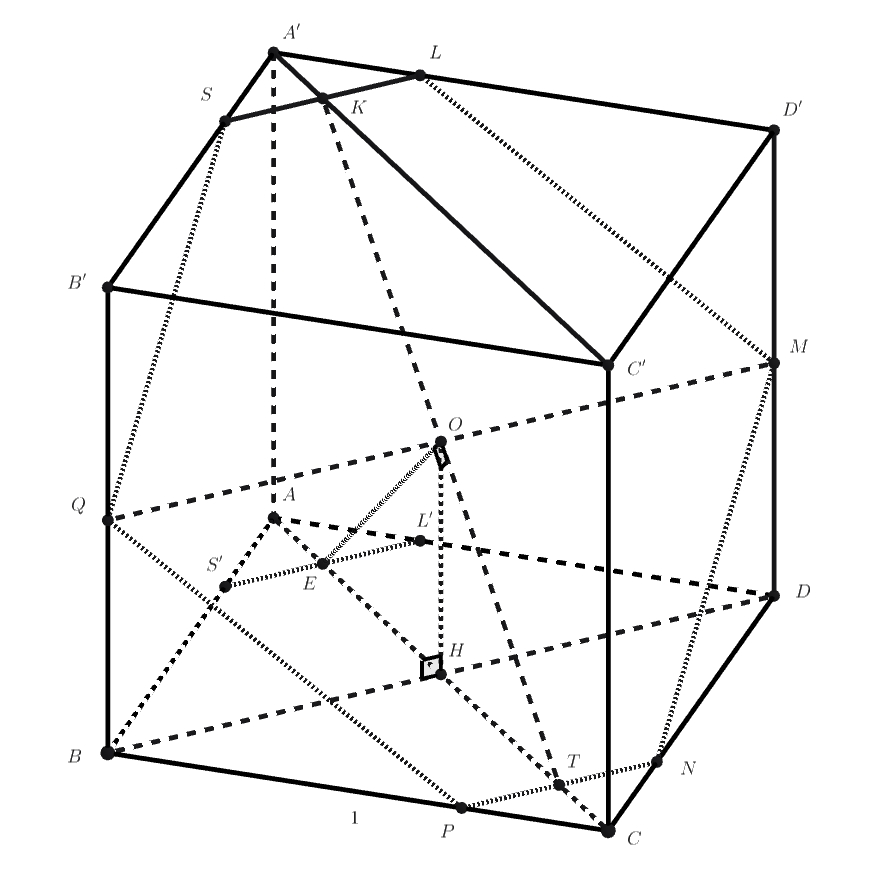
Заметим, что проекция на плоскость
перпендикулярна
следовательно, по ТТП
Проведем через точки
и
прямые, параллельные
точки пересечения этих прямых со сторонами квадратов
и
соответственно
принадлежат сечению. Если провести через точку
прямую, параллельную
то точки пересечения этой прямой с
и
также будут принадлежать сечению, соединив полученные 6 точек, мы построим наше сечение. Пусть
— построенное сечение,
и
Пусть — проекция точки
на плоскость
Треугольник прямоугольный равнобедренный, соответственно,
Заметим, что угол
так что
и
При этом угол
— угол между плоскостью сечения и
плоскостью
также равен
Спроецируем сечение на плоскость проекциями точек
и
являются точки
и
соответственно, проекции точек
и
назовем
и
Найдём площадь шестиугольника
Из подобия треугольников и
следует, что
Аналогично
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




