Стереометрия на ДВИ
Ошибка.
Попробуйте повторить позже
Сфера касается всех рёбер тетраэдра . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что
. Найдите
Источники:
Подсказка 1
Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---
Подсказка 2
Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?
Подсказка 3
Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!
Расстояния от вершины до точек касания сферы с рёбрами
равны. Обозначим это расстояние
. Соответствующие
расстояния от вершин
обозначим
,
соответственно.
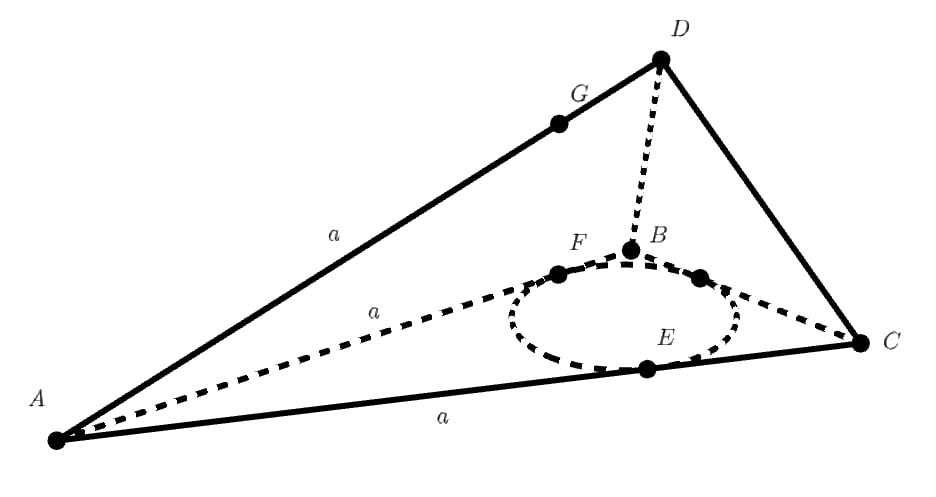
По условию , что равносильно после раскрытия скобок системе
Если , то
, а это не так. Значит,
. Тогда либо
, либо
. Если
, то
, что
противоречит неравенству треугольника. Значит,
и, стало быть,
Замечание.
Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




