Стереометрия на ДВИ
Ошибка.
Попробуйте повторить позже
Дан куб Через середины его ребер
и через центр грани
проведена плоскость, пересекающая
диагональ
куба в точке
. Найдите отношение
:
Источники:
Подсказка 1
Построение этого сечения не выглядит тривиальной задачей. Разберёмся для начала, какие точки этой плоскости нам нужны, чтобы отыскать искомое соотношение. Удобно будет работать с пересечением этой плоскости (назовем ее π) и диагональной (BDD'). Значит нам точно понадобится пересечение π c рёбрами BB' и DD'.
Подсказка 2
Можно заметить, что середина ребра C'D' и центр грани BCC'B' лежат в плоскости диагонального сечения (ABC'). Рассмотрите эту плоскость и поработайте с подобными треугольниками, чтобы определить точку пересечения плоскости π с прямой АВ — зная её, мы сможем посчитать и положение точки пересечения π с ребром BB'.
Подсказка 3
Определить точку пересечения π и DD' тоже не получится в один шаг: удобно это сделать сначала рассматривая всё ту же плоскость (ABC') и прямую AD' в ней. А потом можно будет высчитать и положение точки на DD'.
Подсказка 4
Осталось рассмотреть плоскость (BDD') и имеющуюся у нас теперь прямую её пересечения с π. Поработайте с подобными треугольниками, чтобы отыскать то самое соотношение DO:OB'
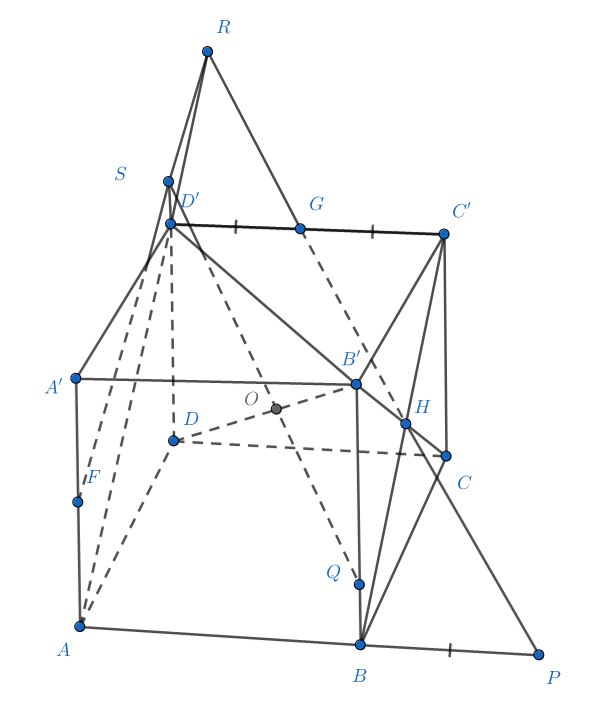
Обозначим середины ребер и центр грани
через
, соответственно. Обозначим также через
плоскость
.
Найдем точку пересечения плоскости
и прямой
. Точки
лежат в плоскости
, следовательно прямые
и
пересекаются. Пусть
- точка их пересечения. Тогда
, поскольку треугольники
и
равны.
Точки
и
принадлежат
, следовательно, прямая
есть прямая пересечения плоскости
с
. То есть
лежит на отрезке
. Из подобия треугольников
и
следует, что
. Следовательно,
.
Найдем теперь точку пересечения плоскости
и прямой
. Прямая
лежит в плоскости
, равно как и прямая
.
Обозначим через
точку пересечения этих прямых. Из подобия треугольников
и
следует, что
. Точки
и
принадлежат
, следовательно, прямая
есть прямая пересечения плоскости
с
. То есть
лежит на продолжении
отрезка
за точку
. Из подобия треугольников
и
следует, что
. Следовательно,
.
Прямая есть прямая пересечения плоскости
с
, то есть она проходит через
. Треугольники
и
подобны с
коэффициентом подобия
. Следовательно,
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




