Планиметрия на МВ (Финашке)
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена высота
, а на сторонах
и
выбраны точки
и
так, что прямые
и
симметричны друг другу относительно прямой
. Прямые
и
пересекаются в точке
. Найдите длину отрезка
,
если
.
Источники:
Подсказка 1
Если прямые AN, CM и BH не пересекаются в одной точке, то чертеж получается нагруженный и неприятный, и не понятно, что с ним вообще делать..( Попробуйте доказать, что эти прямые пересекаются в одной точке.
Подсказка 2
Доказательства этого факта может быть не самым очевидным, однако оно является ключевым в решении задачи. Например, в этом может помочь теорема Бланше.
Подсказка 3
Так, теперь у нас есть три чевианы, пересекающиеся в одной точке.. на какую теорему это нам намекает?
Подсказка 4
Верно, на теорему Чевы! А далее мы можем использовать теорему Менелая, чтобы найти длину искомого отрезка.
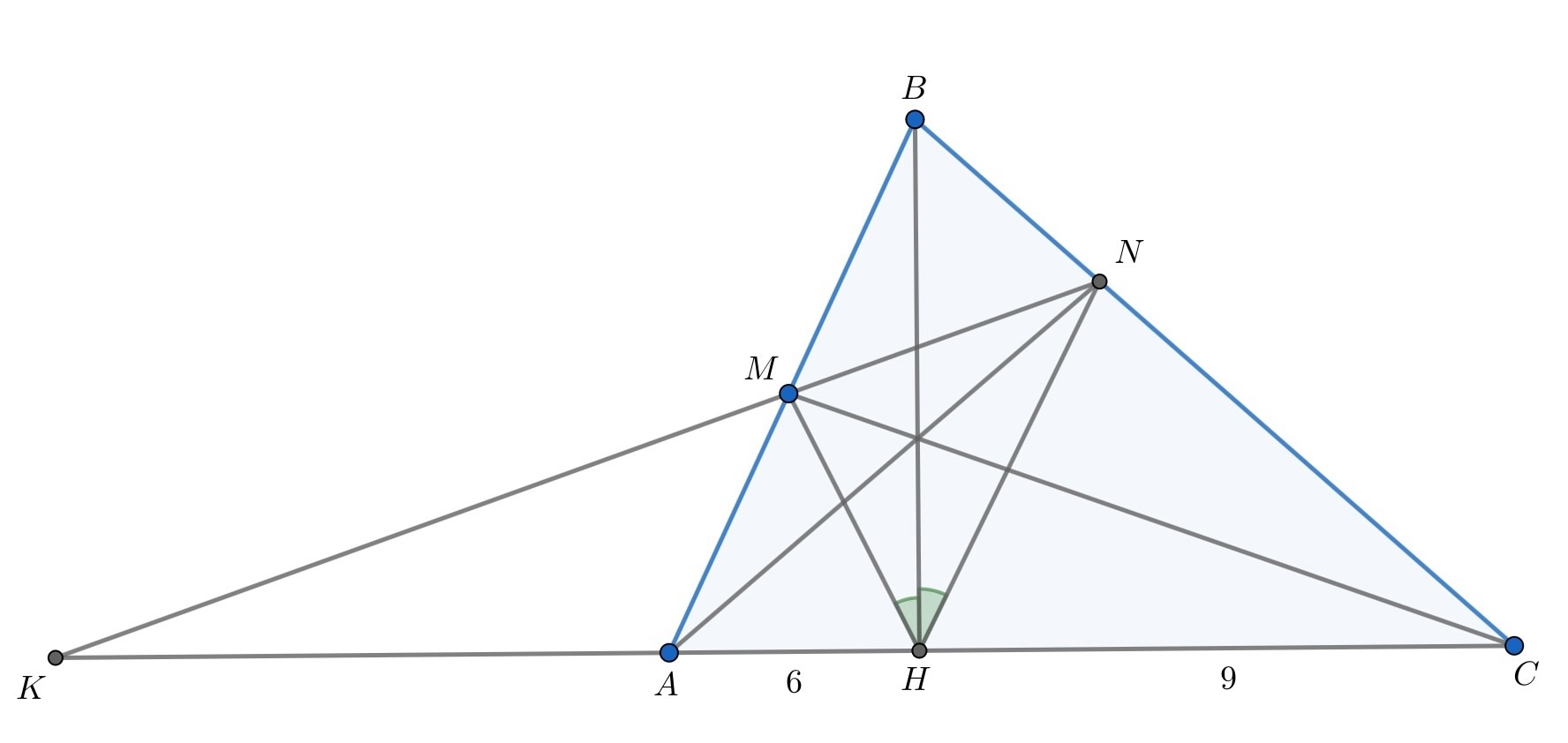
По теореме Бланше симметричность и
относительно высоты
равносильно конкурентности чевиан
то есть
и
пересекаются на высоте
Тогда по теореме Чевы для треугольника
А по теореме Менелая для треугольника и прямой
Из этих двух равенств получаем
Подставляя данные в условии числа,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




