Стереометрия на МВ (Финашке)
Ошибка.
Попробуйте повторить позже
Все вершины тетраэдра равноудалены от точки
. Зная, что
найдите радиус сферы,
проходящей через
и через середины рёбер
и
Источники:
Подсказка 1
Важная идея при работе с тетраэдрами — это достроить тетраэдр до параллелепипеда. Если мы сделаем так в этой задаче, то какой параллелепипед получится?
Подсказка 2
Верно, прямоугольным! А где будут располататься точки, через которые проходит искомая сфера?
Подсказка 3
Да, это центр параллелепипеда и середины его граней! При этом диаметр нашей сферы — это отрезок, соединяющий точку O и одну из вершину параллелепипеда.
Подсказка 4
Что нам дают длины диагоналей граней параллелепипеда? На этом деле квадрат этой длины — это сумма квадратов длин двух некоторых рёбер. Используйте это, чтобы найти искомый радиус.
Достроим тетраэдр до параллелепипеда
, проведя через его противоположные рёбра пары
параллельных плоскостей.
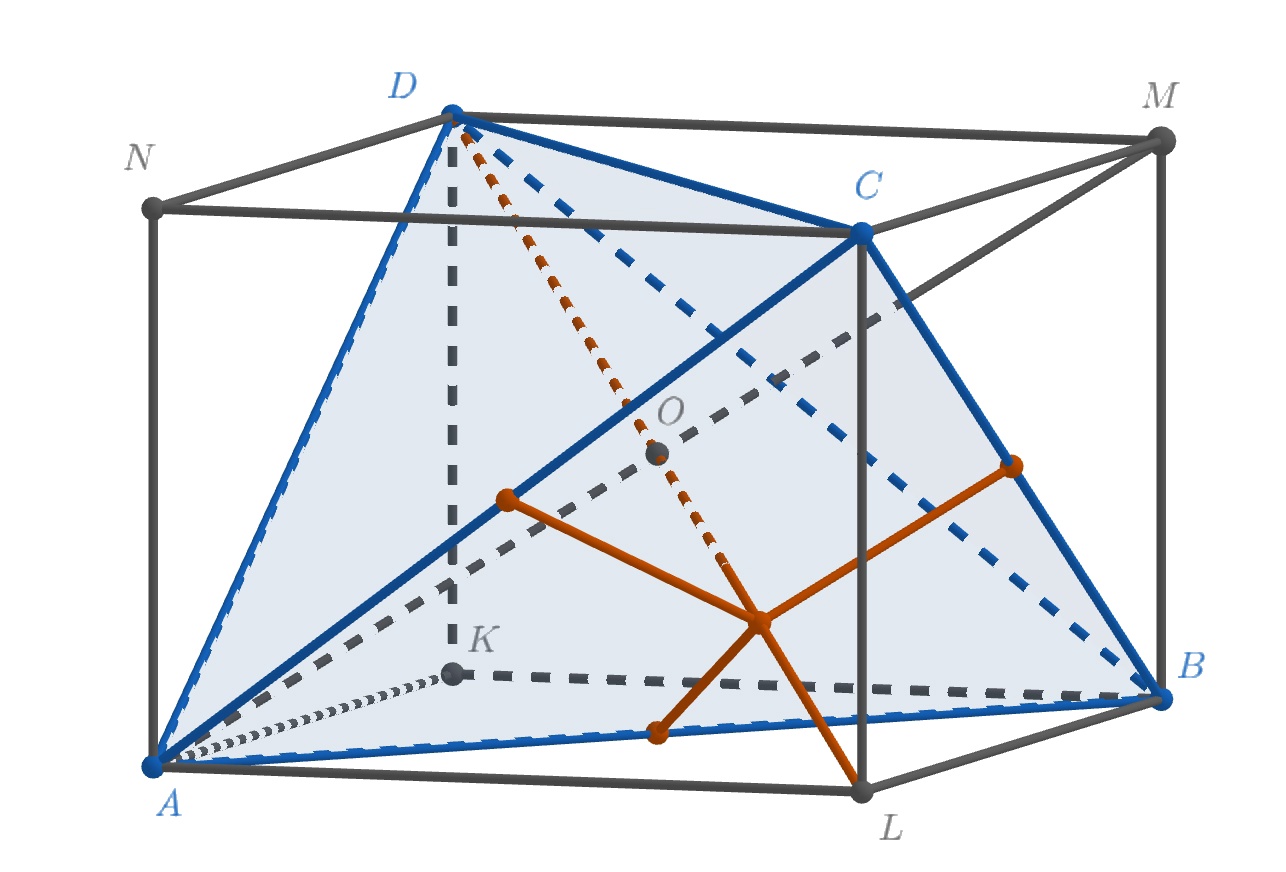
Ввиду равенств и
все грани этого параллелепипеда будут прямоугольниками, а сам
параллелепипед — прямоугольным; точка
окажется его центром, а середины рёбер
и
— центрами граней
и
соответственно.
Bce эти центры принадлежат сфере, построенной на отрезке как на диаметре. Следовательно, искомый радиус
равен
Учитывая, что
получаем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




