Тема МВ / Финашка (Миссия выполнима. Твоё признание — финансист)

Стереометрия на МВ (Финашке)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела мв / финашка (миссия выполнима. твоё признание — финансист)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#81377

Длина ребра куба $ABCDA ′B′C′D′$ равна 1. Найдите радиус сферы, проходящей через точку $B$ и касающейся прямых $AD,AA′$ и $′ ′ A B$ .

Источники: Миссия выполнима - 2024, 11.4 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.

Подсказка 2

Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?

Подсказка 3

Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?

Подсказка 4

Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать

Показать ответ и решение

Введём декартову систему координат с центром в точке $A$ , ось абсцисс — луч $AD$ , ось ординат — луч $AA ′$ , ось аппликат — луч $AB$ .

Пусть $′ O$ — проекция центра сферы на грань $′ ′ AA B B$ куба. Определим ее местоположение. Так как сфера касается прямых $′ ′′ AA ,A B$ и проходит через точку $B$ , то расстояние от точки $′ O$ до прямых $′ AA$ и $′ ′ A B$ и точки $B$ одинаково (обозначим его $r$ ). Тогда $′ O$ лежит на луче $′ A B$ , который является биссектрисой угла $′ ′ AA B$ . Осталось учесть условие, что центр сферы касается прямой $AD$ , то есть нужно проверить, что расстояние от центра до прямой $AD$ совпадает с радиусом сферы $OB$ .

Заметим, что есть два случая расположения точки $′ O$ (на рисунке показаны разными цветами):

$PIC$

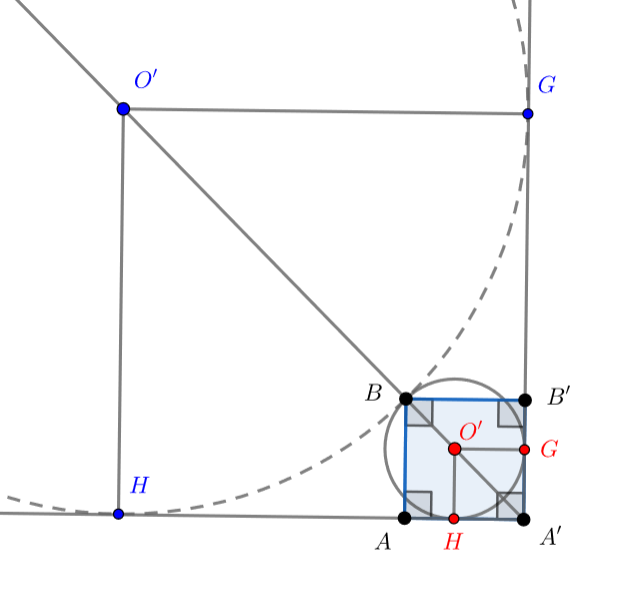
Случай 1: точка $O ′$ лежит на диагонали $A ′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-− r)2$ , откуда $r =2− √2$ . Значит, центр сферы $O$ имеет координаты $(x1;√2-− 1;2− √2)$ .

Расстояние до прямой $AD$ равно $∘(√2−-1)2-+(2−-√2)2$ . То есть радиус $OB = ∘(√2-− 1)2+(2−-√2)2 = ∘9−-6√2.$

Случай 2: точка $O ′$ лежит на продолжении луча $A′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-+r)2$ , откуда $r =2+ √2$ . Значит, центр сферы $O$ в этом случае имеет координаты $(x ;−√2-− 1;2+ √2) 2$ .

Расстояние до прямой $AD$ равно $∘--√-----2-----√--2 (− 2− 1) + (2+ 2)$ . То есть радиус $∘ --√----2-----√--2- ∘ ---√-- OB = (− 2− 1)+ (2+ 2) = 9+6 2.$

Ответ:

$∘9-±-6√2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#63948

На поверхности правильного тетраэдра $ABCD$ построена замкнутая линия, каждая точка $X$ которой обладает следующим свойством: длина кратчайшего пути по поверхности тетраэдра между $X$ и серединой ребра $AB$ равна длине кратчайшего пути по поверхности тетраэдра между $X$ и серединой ребра $CD$ . Найдите длину этой линии, если длина ребра тетраэдра равна 1.

Источники: Миссия выполнима - 2023, 11.4 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

У нас тут рассматривается расстояние по поверхности...Как можно перевести картинку на плоскость в таком случае, чтобы было более удобно?

Подсказка 2

Рассмотреть развертку! Вот пусть мы развернули его так, что получился ромб ABCD, где AC - общее ребро у развернутых граней. Но все еще непонятно как работать с линиями ломаной, которые не получится нормально нарисовать на развертке. Что можно в таком случае придумать?

Подсказка 3

Давайте мысленно "порежем" нашу ломаную ребрами и отрезками AN, BN, CM, DM, где M и N - середины AB и CD, и рассмотрим только ту часть ломаной, что внутри треугольника AMC на нашей развертке. Наверное, в этом треугольнике не сложно найти такие точки на развертке?

Подсказка 4

Например, пусть P - точка ломаной внутри AMC. Понятно, что кратчайший путь от P до M - это PM, а кратчайший путь от P до N - это отрезок PN). Такие отрезки должны быть равны, а значит какое ГМТ у P?

Подсказка 5

Серединный перпендикуляр к MN! Достаточно легко теперь найти длину этой ломаной внутри AMC. А что делать с остальными частями этой ломаной? Вот что: попробуйте осознать, что они будут такими же, например, из соображений симметрии)

Показать ответ и решение

Пусть $M$ и $N$ — середины ребер $AB$ и $CD$ соответственно. Из соображений симметрии ясно, что ребрами $AC,BC, BD,AD$ и отрезками $AN, BN,CM, DM$ линия, о которой идет речь в условии задачи разбивается на 8 равных. Поэтому достаточно рассмотреть точки, принадлежащие треугольнику $AMC$ .

$PIC$

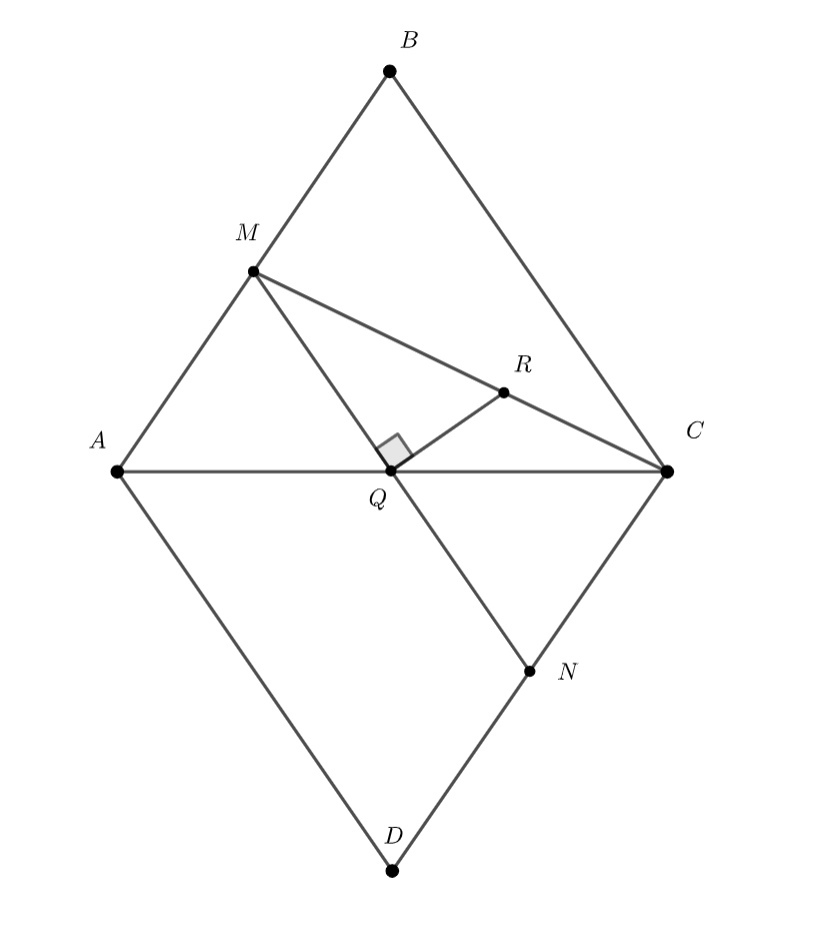
Пусть $P$ - одна из таких точек. Тогда кратчайшим путем между $P$ и $M$ служит отрезок $PM$ , а кратчайшим путем между $P$ и $N$ - двухзвенная ломаная $PKN$ , вершина $K$ которой принадлежит ребру $AC$ (в случае $P ∈AC$ имеем просто отрезок $PN)$ . На развертке тетраэдра объединение граней $ABC$ и $ADC$ представляет собой ромб $ABCD$ , а ломаная $PKN$ - отрезок $PN$ в нем. Условие $P M =P N$ означает, что $P$ лежит на серединном перпендикуляре к отрезку $MN$ ; следовательно геометрическим местом точек $P$ служит отрезок $QR$ , где $Q$ - середина ребра $AC$ (и середина отрезка $MN$ ) $R$ - точка на отрезке $MC$ , $∠MQR = 90∘$ (см рисунок).

Найдем длину отрезка $QR$ . Легко видеть, что $∠QMR = 30∘$ , а отрезок $QM$ , будучи средней линией треугольника $ABC$ , имеет длину $1 2$ . Поэтому $QR = 1tg30∘ = √3 2 6$

Умножив это число на 8, получим ответ к задаче: $4√3- 3$

Ответ:

$4√3 3$

Ошибка.
Попробуйте повторить позже

Задача 3#76529

Через каждую пару противоположных рёбер куба проведена плоскость. На сколько частей эти плоскости разбивают куб?

Источники: Миссия выполнима - 2022, 11.2 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Нам довольно трудно представить разбиение на части внутри куба, так что давайте начнём с рассмотрения граней. Как проведённые плоскости разобьют поверхность куба?

Подсказка 2

Да, каждая грань делится плоскостями на 4 треугольника, соответственно вся площадь делится на 24 части. Теперь можем подумать о том, как плоскости разделяют фигуру внутри. Будут ли образовываться такие "внутренние" части, у которых нет общих точек с поверхностью?

Подсказка 3

Да, получаем, что все плоскости пересекаются в центре, при этом каждой части соответствует ровно один треугольник с поверхности. Какой мы из этого можем сделать вывод?

Показать ответ и решение

$PIC$

Каждая такая плоскость проходит через пару параллельных диагоналей противоположных граней куба. Поэтому каждая грань разбита на $4,$ а вся поверхность куба —на $4⋅6$ треугольника, каждые два из которых отделены друг от друга хотя бы одной из проведённых плоскостей. А поскольку все проведённые плоскости пересекаются в центре куба, то каждая часть содержит в качестве одной из своих граней один из этих $24$ треугольников. Следовательно, число частей разбиения также равно $24.$

Ответ: 24

Ошибка.
Попробуйте повторить позже

Задача 4#76531

$A′,$ $B′$ и $C′$ — проекции вершины $S$ правильной треугольной пирамиды $SABC$ на биссекторные плоскости двугранных углов при рёбрах $BC,$ $AC$ и $AB.$ Найдите тангенс каждого из этих углов, если объём пирамиды $′ ′ ′ SA BC$ в $10$ раз меньше объёма пирамиды $SABC.$

Источники: Миссия выполнима - 2022, 11.4 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Сходу непонятно, что делать с условием на перпендикуляры к плоскостям, может, попытаться сделать какое-то дополнительное построение, связанное с вершиной S и одной из этих плоскостей?

Подсказка 2

Правильно, сделать симметрию точки S относительно плоскости A'BC и получить точку S₁. Попробуйте получить точки S₂, S₃ по такой же симметрии, только относительно AB'C и ABC'.

Подсказка 3

Мы получили треугольник S₁S₂S₃, кажется, что он концентричен с треугольником ABC (докажите это, используя поворот относительно высоты пирамиды).

Подсказка 4

Треугольник PSS₁ равнобедренный (P - середина BC), так как PA' - высота и биссектриса, а значит SA'=A'S₁, следовательно, пирамида SS₁S₂S₃ является образом SA'B'C' при гомотетии с коэффициентом 2 и центром в S, а значит, как относятся их объемы?

Подсказка 5

Правильно, в 8 раз. Теперь мы можем использовать условие с отношениями объемов SABC и SA'B'C', найдя отношение объемов SABC и SS₁S₂S₃ и отношение площадей их оснований.

Подсказка 6

Проведём высоту SO нашей пирамиды и найдем отношение S₁O/AO с помощью отношения площадей.

Подсказка 7

Выразим S₁O и OA через SO и найдем тангенс угла, который нужно вычислить в задаче с помощью найденных отрезков.

Показать ответ и решение

Точки $S ,S , 1 2$ и $S 3$ симметричные $S$ относительно биссекторных плоскостей, лежат в плоскости $ABC.$ А поскольку тройка этих биссекторных плоскостей переходит в себя при повороте на $∘ 60$ вокруг оси пирамиды, то этим свойством обладает и тройка точек $S1,S2,S3.$ Следовательно, треугольник $△S1S2S3$ — правильный, и его центр, который мы обозначим через $O,$ совпадает с центром треугольника $△ABC.$

$PIC$

Заметим, далее, что пирамида $SS1S2S3$ —- образ пирамиды $SA′B ′C ′$ при гомотетии с центром $S$ и коэффициентом $2.$ С учётом условия задачи это означает, что отношение объёмов пирамид $SABC$ и $SS1S2S3$ равно $10:23 =5 :4.$ А поскольку у этих пирамид общая высота $SO,$ то и отношение площади треугольника $△ABC$ к площади треугольника $△S1S2S3$ равно $5:4.$ В качестве следствия получается равенство $OA :OS1 = √5 :2,$ которое будет нами использовано.

Обозначив величину двугранного ребра при ребре $BC$ через $φ$ , точкой, симметричной $S$ относительно соответствующей биссекторной плоскости будем считать $S1.$

$PIC$

Тогда $φ= ∠SPA = ∠SPS1,$ где $P$ — середина ребра $BC$ ; треугольник $△SP S1$ — равнобедренный $(SP = PS1),$ откуда

180∘ − φ φ ∠SS1P = ---2--,OS1 =SO ctg∠SS1P = SOtg2-

А поскольку

OA = 2⋅AP = 2⋅SOctg φ, 2

то

√5 OA 2ctgφ -2-= OS1 =-tg φ2

tg φtgφ = 4√- 2 5

При $0∘ < φ< 90∘$ левая часть последнего равенства равна $∘1+-tg2φ− 1,$ что позволяет найти

∘16+-8√5- tgφ = ---5---

Ответ:

$∘ 16+-8√5 ---5---$

Ошибка.
Попробуйте повторить позже

Задача 5#96829

Около шара радиуса $1$ описана правильная $n$ -угольная призма, все ребра которой касаются некоторого другого шара. Докажите, что $n =4$ и найдите объём этой призмы.

Источники: Миссия выполнима - 2021, 11.6 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

В этой задаче самое главное — связать боковую сторону и сторону многоугольника основания. Так как в основании у нас правильный многоугольник, в который вписана окружность радиуса 1, то чему в этом случае равна сторона основания? А какой факт можно извлечь из того, что вторая сфера касается каждого ребра?

Подсказка 2

В этом случае, сторона равна 2tg(pi/n) — просто опускаем высоту из центра на какую-нибудь сторону и вычисляем. А вот из того, что вторая сфера касается каждого ребра, следует, что прямоугольник боковой стороны является описанным. Осталось связать этот факт и тот, что в призму вписана сфера с радиусом 1, и получим ответ!

Показать ответ и решение

Высота призмы и боковое ребро равны $2$ (диаметру вписанного шара). Основания призмы являются правильными $n$ -угольниками, описанными около окружностей радиуса $1.$ Согласно известной формуле, сторона основания в этом случае равна $π 2tg n.$ Поверхность шара, касающегося рёбер призмы, пересекает каждую из граней по окружности. Это значит, что прямоугольники, служащие боковыми гранями, описанные, а потому являются квадратами. Отсюда $π 2tgn =2$ и $n =4.$