18.03 Робот-сборщик – ямы и/или стены
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. В любой клетке поля может быть стена (стены обозначены
значениями больше 100) или яма (ямы обозначены значениями меньше 0). При попытке зайти на клетку со стеной
Робот разрушается. При попытке зайти на клетку с ямой Робот застревает в ней и не может двигаться
дальше. Определите максимальную и минимальную денежную сумму, которую может собрать Робот,
пройдя из левой верхней клетки в правую нижнюю, не разрушившись и не застряв в яме. Известно, что
такой путь существует. В ответе укажите два числа без пробела – сначала максимальную сумму, затем
минимальную.
Открываем файл с таблицей. Чуть ниже основной таблицы начинаем создавать свою, в которой будем производить все
вычисления. Так как робот идет из верхней левой в правую нижнюю клетку, и эта клетка удовлетворяет условиям
нашей задачи, переписываем её без изменений. Затем прописываем формулу для первой строки и для первого столбца,
учитывая, что могут быть ямы и стены (если там встретилась яма или стена, то все монеты за ней он уже не сможет
собрать). Проверяем ячейку В1, если меньше 0 или больше 100, то это яма/стена. Нас не это устраивает, и мы пишем
очень маленькое число, иначе прибавляем ее к предыдущей ячейке. Растягиваем эту формулу на всю
строку.

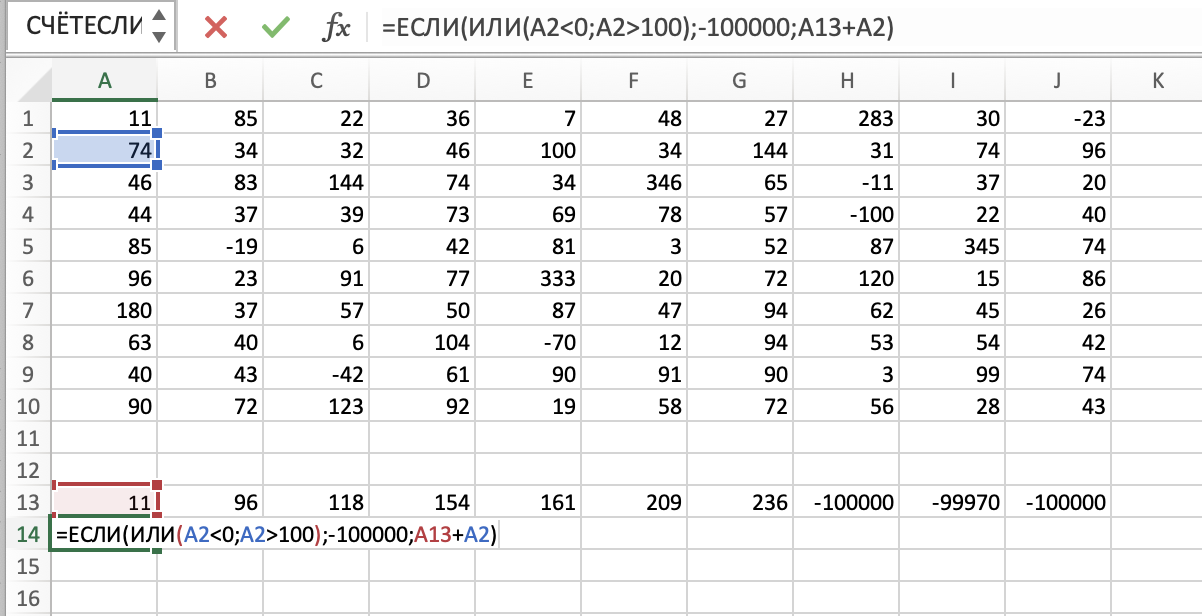
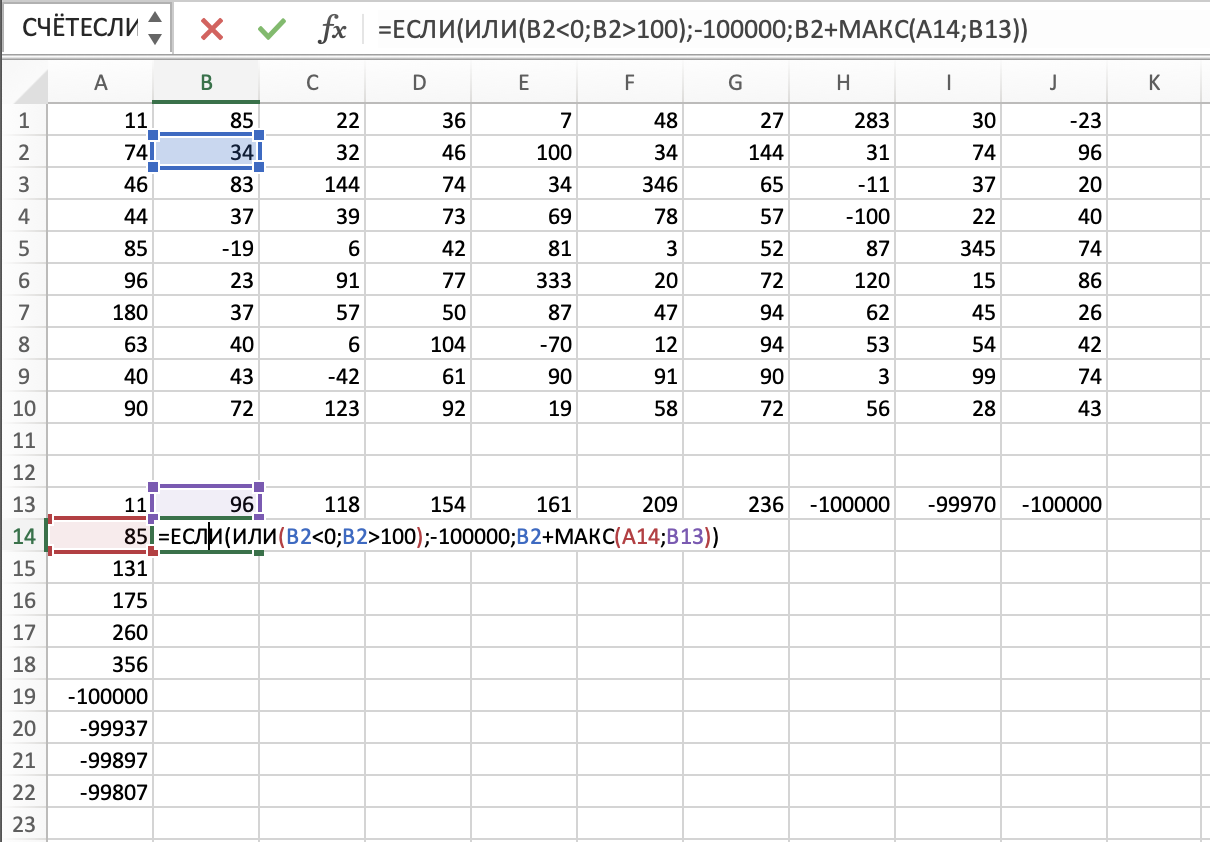
Теперь заполняем остальные ячейки. Найдем максимальную сумму. В ячейке B15 пишем:
=ЕСЛИ(ИЛИ(В2<0;B2>100) -100000; B2+МАКС(B13;A14)).
Растягиваем эту формулу на диапазон В14:J22. В правой нижней ячейке J22 и будет искомая максимальная сумма. Она
равна 1242.
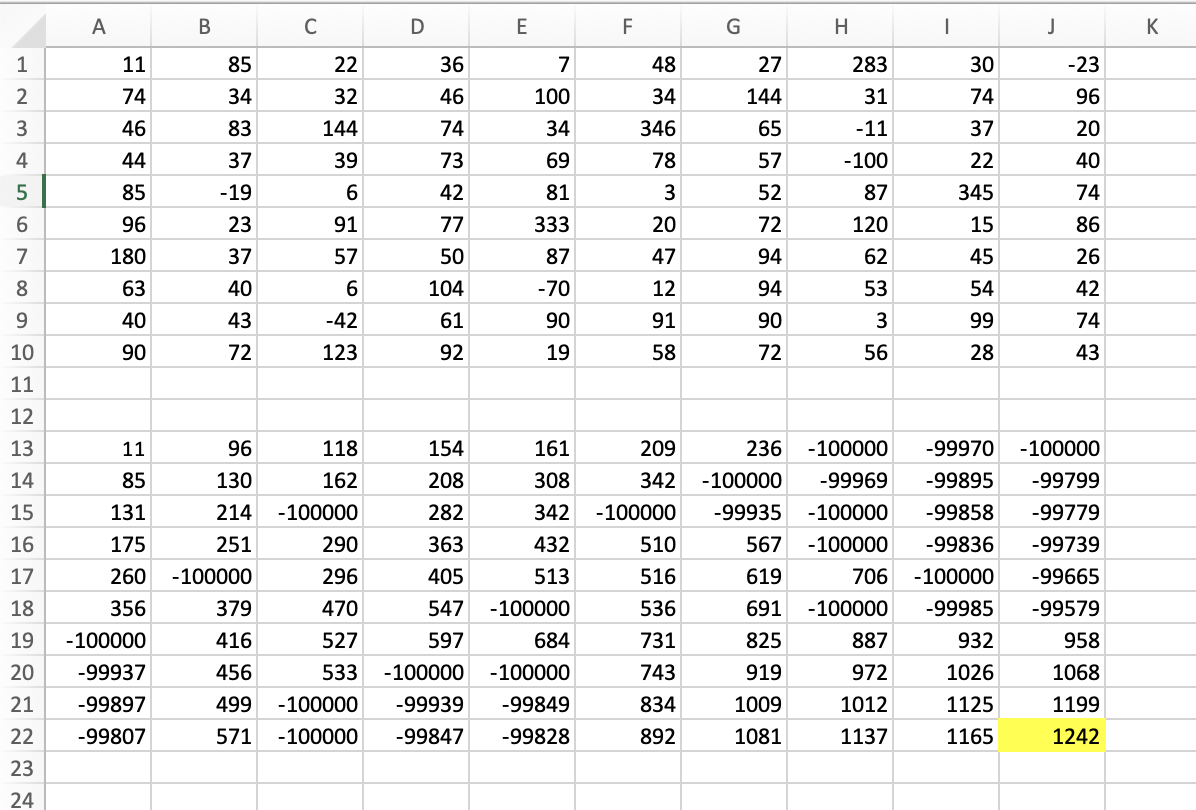
Для того, чтобы найти минимальную сумму необходимо заменить во всех формулах -100000 на какое-либо большое число (например, 100000), а также заменить МАКС на МИН. Минимальная сумма равна 739. Тогда в ответ пойдет: 1242739
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





