15.03 Неравенства

Аналитическое решение

Упростим выражение, раскрыв импликацию:

Нарисуем полученные неравенства на числовых осях:

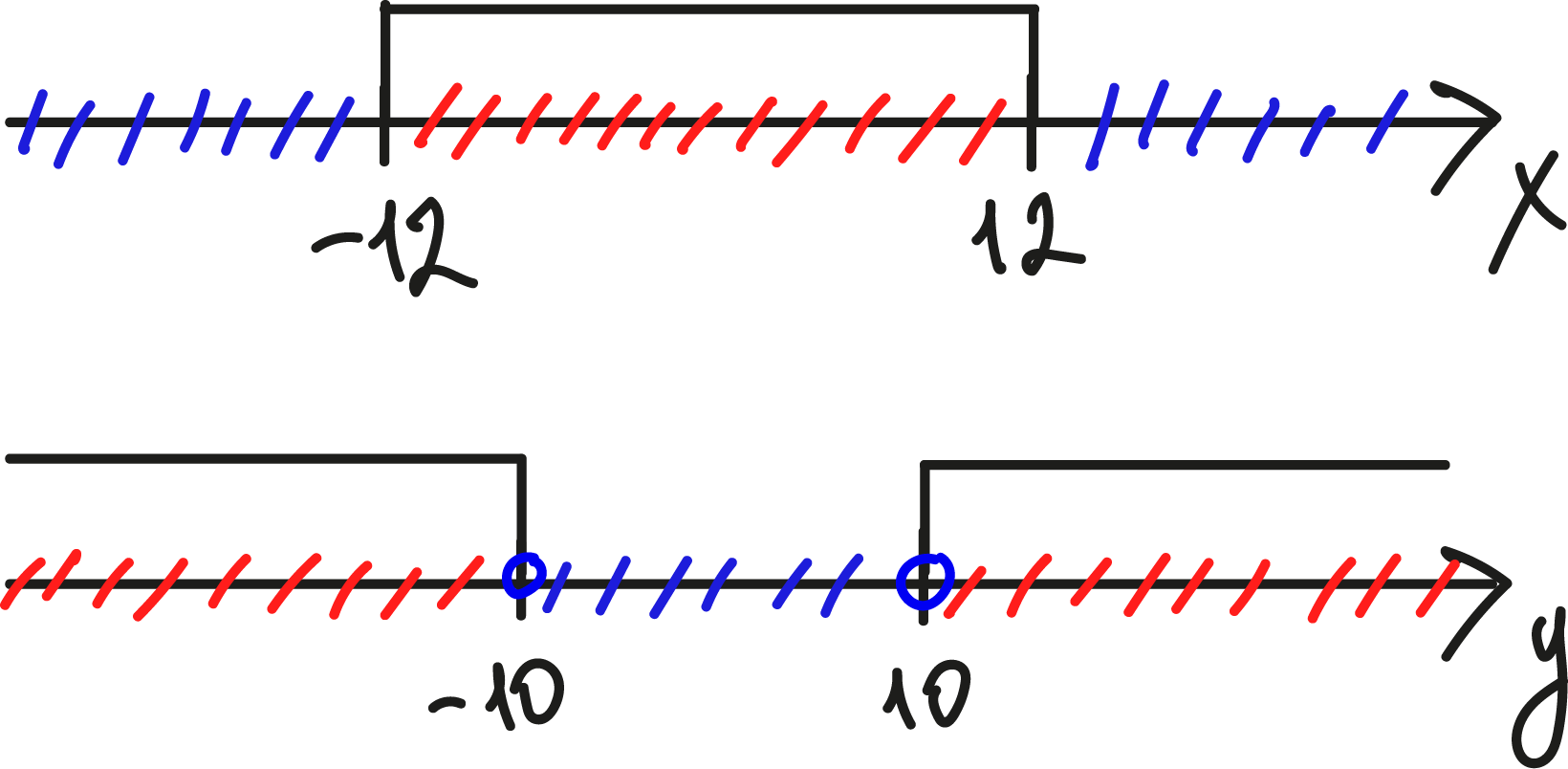
Красным на этом рисунке выделены области, которые перекрываются известной частью выражения, а синей те части, которые необходимо перекрыть отрезком . Так как и , то наибольший отрезок, которым может быть это [-12; 12]. Так как если сделать его еще больше, то будут точки на оси для которых выражение не будет являться истиной. Длина этого отрезка – 24.

Идея решения:

Перебираем все возможные отрезки в заданном диапазоне вещественных чисел. Для каждого такого отрезка проверяем тождественную истинность формулы для множества точек и с определённой дискретизацией (например, с шагом 0.25):

- Если для какого-либо или формула не выполняется, текущий отрезок отбрасываем. - Если формула выполняется для всех перебранных точек, отрезок считается подходящим, и мы обновляем максимум длины .

После перебора всех вариантов отрезков максимальная найденная длина будет наибольшей возможной длиной отрезка , при которой формула тождественно истинна.

Решение программой:

maxLen = 0  # Наибольшая длина отрезка A

# Перебор целых значений для a и b с шагом 0.25, поэтому умножаем на 4
for a in range(-30, 30 + 1):
    for b in range(a, 30 + 1):
        ok = 1  # Флаг, показывает, что отрезок подходит

        # Перебор x с шагом 0.25
        for x in range(-30*4, 30*4 + 1):
            x /= 4
            # Перебор y с шагом 0.25
            for y in range(-30*4, 30*4 + 1):
                y /= 4
                # Проверяем тождественную истинность формулы для текущих x, y
                F = ((a <= x <= b) <= (x**2 <= 144)) and ((y**2 <= 100) <= (a <= y <= b))
                if F == 0:  # Если формула не выполняется
                    ok = 0  # Отрезок не подходит
                    break  # Прерываем перебор y

            if ok == 0:  # Если формула не выполняется, прерываем перебор x
                break

        if ok == 1:  # Если отрезок подошёл для всех x и y
            maxLen = max(maxLen, (b - a))  # Обновляем максимальную длину

print(maxLen)  # Выводим наибольшую возможную длину отрезка A