.06 Теория графов. Лемма о рукопожатиях. Связность. Эйлеровость.

Для наглядности представим себе карту нашего города в виде графа, в которой улица - это ребро такого квадратика.

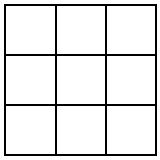
Ясно, что нам нужно обойти все улицы. В самом лучшем случае, то есть в том случае, если бы нам удалось обойти весь граф, пройдя каждое ребро лишь один раз, у нас получилось бы метров. Но можем ли мы так сделать? То есть, иными словами, будет ли наш граф эйлеровым?

Заметим, что у нас есть целых 8 вершин степени 3. А это слишком много. Эйлеров граф может содержать либо 0, либо 2 вершины нечетной степени. Следовательно, наш граф - не эйлеров, и поэтому не получится обойти его весь, пройдя по каждому ребру лишь один раз - наш идеальный случай с 7200 метрами недостижим.

Эти 8 вершин степени 3, они плохие. Ведь мы должны начать и закончить в левой нижней точке нашего города, то есть эти 8 вершин степени 3 будут промежуточными.

А промежуточная вершина нашего потенциального пути, проходящего по всем ребрам лишь один раз, не может иметь нечетной степени. В промежуточную вершину мы должны зайти столько же раз, сколько и выйдем из неё.

Следовательно, каждая из этих 8 вершин степени 3 даст обязательно какое-то ребро, по которому мы пройдем дважды. И что же. получается, будет еще 8 лишних проходов?

Нет, не обязательно. Соседние вершины степени 3 могут давать один и тот же лишний проход - так можно сэкономить и сделать лишь 4 лишних прохода, а вот дальше уже сэкономить, очевидно, никак нельзя. Таким образом, получается 4 лишних прохода, поэтому наша оценка получилась такой:

Но это лишь оценка, а вдруг и такого пути не существует, но уже по каким-то другим, более тонким причинам?

На самом деле, существует, и сконструировать его не так-то сложно