Тема Бельчонок

Планиметрия на Бельчонке

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бельчонок

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#86095

На окружности по часовой стрелке поставлены точки $A$ , $B$ , $C$ , $D$ , $E$ . Известно, что $AE =DE$ . Пересечение отрезков $AC$ и $BD$ обозначим через $P$ . На продолжении отрезка $AB$ за точку $A$ выбрали точку $Q$ так, что $AQ = DP$ . На продолжении отрезка $CD$ за точку $D$ выбрали точку $R$ так, что $AP = DR$ . Докажите, что прямые $P E$ и $QR$ перпендикулярны.

Источники: Бельчонок - 2024, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Угол BAP равен углу BDC как вписанный, а значит углы QAP и RDP тоже равны. Треугольники QAP и RDP равны, тогда PQ=QR.

Подсказка 2

Попробуем выделить равные уголки за счет вписанных четырёхугольников ACDE и ABDE. Каким углам равны соответственно RDE и QAE?

Подсказка 3

Что можно сказать про треугольники RDE и EAP, а также EQA и EDP? Они равны по 2 сторонам и углу между ними. Следовательно QE=RE=PE, тогда что можно сказать про точку E?

Подсказка 4

Е — центр описанной окружности, а следовательно PE — часть биссектрисы в равнобедренном треугольнике, а следовательно и часть высоты

Показать доказательство

Отметим равные углы: $∠BAP = ∠BDC,$ как вписанные углы, отсюда следует, что $∠P AQ= ∠P DR.$ Рассмотрим треугольники $△P AQ$ и $△P DR.$ У них равны две стороны и угол между этими сторонами. Следовательно, эти треугольники равны, тогда $PQ = PR.$ Тогда нужно доказать , что $QE$ является частью высоты в равнобедренном треугольнике.

$PIC$

Рассмотрим вписанные четырехугольники $ACDE$ и $ABDE.$ Из вписанности получаем $∠PAE = ∠EDR$ и $∠PDE = ∠EAQ.$ Рассмотрим треугольники $△AP E$ и $△DRE.$ У них равны две стороны и угол между этими сторонами. Следовательно, эти треугольники равны, тогда $PE = ER.$ Используя аналогичные рассуждения для треугольников $△PDE$ и $△QAE,$ получаем что $P E = QE.$

В итоге получили, что точка $E$ равноудалена от вершин треугольника $△P QR,$ то есть является центром описанной окружности равнобедренного треугольника. Следовательно, $PE$ является частью высоты треугольника $△PQR,$ то есть $P E ⊥ QR.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#86100

Окружности $w 1$ и $w 2$ пересекаются в точках $A$ и $B.$ Прямая $l$ расположена ближе к $A$ , чем к $B$ , и является общей касательной окружностей $w1$ и $w2$ , касаясь их соответственно в точках $T$ и $R$ . Через точку $A$ проведена параллельно касательной $l$ прямая, пересекающая $w1$ в точке $C,w2$ в точке $D$ . Прямые $TC$ и $RD$ пересекаются в точке $E,$ прямые $T B$ и $CD$ пересекаются в точке $M,$ прямые $RB$ и $CD$ пересекаются в точке $N.$ Докажите, что $TBRE$ — вписанный четырёхугольник.

Источники: Бельчонок - 2024, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Поставим цель доказать, что противоположные углы в четырёхугольнике TBRE в сумме дают 180 градусов. Чтобы сделать это, воспользуемся свойствами вписанных четырёхугольников, которые уже есть на картинке, и отметим в них равные уголочки.

Подсказка 2

У нас есть пары углов СТВ, САВ и BAD, BRD, которые опираются на одну дугу. Воспользуется свойствами смежных углов и докажем то, что хотели! Даже свойства касательных не понадобились.

Показать доказательство

Пусть $∠BT E =α,$ а $∠BRE = β.$ Тогда смежные с ними $∠BTC = 180∘− α,∠BRD = 180∘− β.$

______________________________________________________________________________________________________________________________________________________

$PIC$

Замечание. Точки $M$ и $N$ не подписаны на чертеже, потому что в решении их использовать не будем.

_________________________________________________________________________________________________________________________________________________________________________________

В силу вписанности $ABCT$ и $ABDR$ получаем

∠BAC = ∠BTC = 180∘ − α, ∠BAD = ∠BRD = 180∘− β

Но $∠BAC$ и $∠BAD$ смежные, поэтому

(180∘ − α)+ (180∘− β)=180∘

Следовательно, $∠BTE +∠BRE =α +β = 180∘,$ так что $TBRE$ вписанный.

Ошибка.
Попробуйте повторить позже

Задача 3#69400

Дан прямоугольный треугольник $KLM$ с прямым углом $M.$ На его катете $LM$ длины 52 как на диаметре построена окружность $ω.$ Из точки $K$ к этой окружности проведена касательная $KD,$ отличная от $KM.$ Перпендикуляр $DH,$ опущенный на отрезок $LM,$ пересекает отрезок $KL$ в точке $E.$ Найдите площадь треугольника $LDE,$ если известно, что $LH :MH =4 :9.$

Источники: Бельчонок-2023, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Для начала попробуем найти всё, что можем)) Воспользуемся всеми условиями на LH, LM, MH и найдем их) Тогда будет несложно найти оставшиеся отрезки на LM и DH! На картинке много прямых углов...что хочется сделать?

Подсказка 2

Найти среди них подобные! Учтём, что угол между касательной и радиусом прямой, тогда какие треугольники будут подобными (или даже равными)?

Подсказка 3

Треугольники MKO и KOD будут равными, тогда треугольники LHD и OKM будут подобны! Найдём отношение KM/LM. Теперь нам необходимо найти площадь треугольника LED, как можно это сделать?

Подсказка 4

Найдя его высоту и стороны! Высота его это LH, а в каких подобных треугольниках этот отрезок встречается, чтобы его найти?

Подсказка 5

Треугольники LHE и LMK подобны, поэтому несложно найти EH! Осталось лишь найти DE через DH и EH, что сделать из подобия несложно)

Показать ответ и решение

$PIC$

Пусть $O$ — центр окружности $ω.$ Заметим, что

∘ --------- LH =-4LM =16, MH = 36, OH = 1LM − LH = 10, DH = OD2 − OH2 = 24 13 2

Прямоугольные треугольники $LHD$ и $OMK$ подобны, поскольку

∠MLD = 1∠MOD = 1(180∘ − ∠MKD )= 90∘ − ∠MKO = ∠MOK 2 2

Тогда

KM-- 1 KM-- 1 DH- 3 LM = 2 ⋅OM = 2 ⋅LH = 4

Из подобия треугольников $LHE$ и $LMK$ мы получаем

3 EH = 4LH = 12

Поэтому

1 1 1 SLDE = 2 ⋅DE ⋅LH = 2 ⋅(DH − EH )⋅LH = 2 ⋅12⋅16 =96

Ответ: 96

Ошибка.
Попробуйте повторить позже

Задача 4#69405

В треугольник $ABC$ вписана окружность $ω$ радиуса $r,$ которая касается стороны $AB$ в точке $P.$ На окружности отмечена точка $R,$ диаметрально противоположная точке $P.$ Прямая $CR$ пересекает сторону $AB$ в точке $Q,$ причём $CA + AQ =1.$ Найдите площадь треугольника $ABC.$

Источники: Бельчонок-2023, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Для начала хочется понять: что вообще делать с условием CA + AQ = 1? Перекинуть равенство на один отрезок - так себе идея. Давайте найдём это же равенство в треугольнике еще раз! Например, попробуем доказать, что CB + BQ = 1) Что можно сделать?

Подсказка 2

Если бы треугольники CBQ и CAQ состояли из касательных к окружности, то было бы удобнее разбираться с этим условием...А может быть, есть треугольники, некоторые стороны которых - касательные к вписанной окружности, и они связаны с CBQ и CAQ?

Подсказка 3

Проведите касательную в точке R к вписанной окружности. С помощью точек пересечения к сторонам треугольника получатся два треугольника. И вот они на самом деле подобны каким-то двум другим треугольникам и обладают очень интересным свойством) Останется применить всё, что знаем, и вспомнить формулу S = pr!

Показать ответ и решение

Проведём через точку $R$ касательную к $ω,$ пересекающую отрезки $AC$ и $BC$ в точках $M$ и $N$ соответственно. Пусть $K$ и $L$ — точки, в которых $ω$ касается сторон $AC$ и $BC$ соответственно.

$PIC$

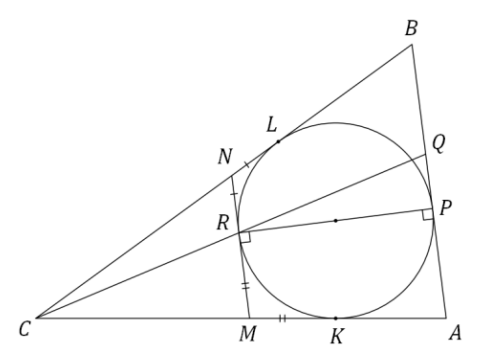
Заметим, что $CM + MR = CM + MK =CK = CL = CN +LN = CN + NR.$ Прямые $AB$ и $MN$ параллельны как перпендикуляры к одному диаметру. Поэтому треугольники $CNR$ и $CBQ,$ а также $CMR$ и $CAQ$ подобны с коэффициентом $k= CCQR.$ Тогда

CB + BQ = k(CN + NR )=k(CM + MR )= CA+ AQ = 1,

откуда

SABC = 1(CA +AB + BC)⋅r= 1(CA +AQ + BQ +CB )⋅r= r 2 2

Ответ:

$r$

Ошибка.
Попробуйте повторить позже

Задача 5#58323

На продолжении за точку $C$ стороны $BC$ равностороннего треугольника $ABC$ выбрана точка $M$ , через неё проведена прямая, параллельная $AC$ . Эта прямая пересекает продолжение стороны $AB$ в точке $N$ . Медианы треугольника $BNM$ пересекаются в точке $O$ . Точка $D$ — середина $AM$ . Найдите углы треугольника $ODC.$

Источники: Бельчонок-2022, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Проведем отрезок АК такой, чтобы АК было параллельно СМ! Заметим, что тогда АКМС это параллелограмм.

Подсказка 2

Давайте заметим, что треугольник BNM правильный, откуда для его центра O: OM = ON ! Тогда мы можем попробовать отметить равные углы и равные отрезки на нашей картинке (их тут много!)

Подсказка 3

Попробуйте доказать, что треугольники KON и COM равны, и, используя, что D - точка пересечения диагоналей параллелограмма, подсчитать углы в треугольнике!

Показать ответ и решение

$PIC$

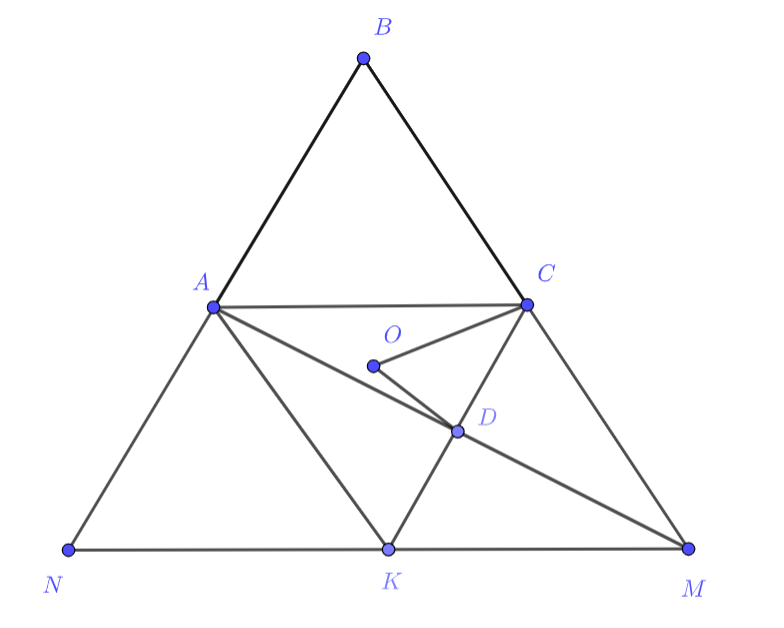
Рассмотрим $K ∈NM, AK ∥CM$ , откуда $AKMC$ — параллелограмм. Заметим, что

В $△AKN :∠N = 60∘,AK ∥BC$ , откуда он равносторонний и $NK = NA =MC$ (в силу симметрии).
Треугольник $BNM$ правильный, откуда для его центра $O$ : $OM = ON$ .
Аналогично предыдущему $∠KNO = ∠N2-= ∠M2-= ∠CMO =30∘$ .

Отсюда по двум сторонам и углу между ними $△KON =△COM$ , тогда $OK = OC$ . Поскольку $D$ является точкой пересечения диагоналей параллелограмма, то $KD =DC$ и $OD$ является медианой равнобедренного $△KOC$ . Отсюда $∘ ∠ODC = 90$ и

∠KOC ∠KOM + ∠MOC ∠KOM +∠KON ∠NOM ∠DOC = --2--= ------2------ = ------2------= ---2-- =60∘

снова пользуясь правильностью $△BNM$ . В итоге получаем $∠OCD = 180∘− ∠DOC − ∠CDO = 30∘$ .

Ответ:

$90∘,60∘,30∘$

Ошибка.
Попробуйте повторить позже

Задача 6#82776

B прямоугольнике $ABCD$ сторона $BC =3.$ На стороне $AB$ отмечена её середина — точка $P.$ Из точки $C$ опущен перпендикуляр $CQ$ на $DP.$ Найдите длину $BQ.$

Источники: Бельчонок - 2022, 11 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Видим, что у нас отмечена середина отрезка, а точку P и DP хотелось бы как-нибудь в целом получше связать с картинкой. Какое тогда дополнительное построение хорошо бы сделать?

Подсказка 2

Верно, давайте продлим DP до пересечения с продолжением BC в точке M. Что тогда можно сказать про прямоугольные треугольники PAD и BPM?

Подсказка 3

Да, они ведь равны по катету и острому углу. То есть мы получаем, что MB=AD=BC. Но нам нужен отрезок BQ. Заметим, что у нас получился ещё один прямоугольный треугольник. Что можно сказать про BQ в нём?

Подсказка 4

Верно, BQ является медианой в нём. Осталось только вспомнить, свойство медианы в прямоугольном треугольнике, и победа!

Показать ответ и решение

Продлим $CB$ и $DP$ до пересечения, пусть $M$ — это точка их пересечения.

$PIC$

Прямоугольные треугольники $MBP$ и $DAP$ равны, так как имеют равные катеты, $BP = AP,$ потому что $P$ — середина, и равные острые углы, $∠MP B = ∠AP D,$ как вертикальные. Значит, $MB = AD = BC.$ Таким образом, $BQ$ — медиана прямоугольного треугольника $MQC,$ и равна половине гипотенузе $MC,$ то есть 3.

Ответ: 3

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#94775

Серединный перпендикуляр к боковой стороне $AC$ равнобедренного треугольника $ABC$ пересекает боковую сторону $AB$ в точке $L$ , а продолжение основания — в точке $K$ . Найдите углы треугольника $ABC$ , если известно, что треугольники $ALC$ и $KBL$ равновелики.

Источники: Бельчонок - 2021, 11.3 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Пусть M — середина АС. Тогда KM — серединный перпендикуляр к АС, что из этого следует? И нас просили найти углы АВС, тогда давайте обозначим ∠ACB = α и посчитаем остальные.

Подсказка 2

Да, AK = CK! Чем являются KL и KM? Что тогда можем записать? Условием про серпер воспользовались, теперь нужно использовать равенство площадей... Треугольники не связаны друг с другом, ничего общего у них нет... Тогда стоит поискать ещё равновеликие треугольники и заменить площадь(-и) △ALC или △KBL на какую-то другую или выразить её через другую. И сделать это так, чтобы у новой пары треугольников было что-то общее.

Подсказка 3

KL и KM — биссектрисы, тогда можно записать равенство отношений! А с площадями воспользуйтесь CM = MA. И запишите, какие произведения равны из равенства площадей. Ну и раз уж мы с отношениями работаем — видите подобные треугольники на картинке?

Подсказка 4

Ага, △ABC ~ △KAC! И из этого мы получаем ещё одно равенство отношений. Но даже если посмотреть на все полученные до этого равенства, мы не сможем сделать какой-то вывод, который поможет решить задачу... И всем, что есть на картинке, мы уже воспользовались. Или нет? Какие теоремы нам помогают, когда хотим найти отношение?

Подсказка 5

Теорема Фалеса (обобщённая), Чевы, Менелая... Какая тут поможет? Можно воспользоваться ей или же сделать доп. построение — провести через M среднюю линию △ABC. Так мы сами создадим пару параллельных прямых для теоремы Фалеса!

Подсказка 6

Менелая можно было применить, к примеру, для △ABC и секущей ML. Фалес помогал для секущих KM и KN. Остаётся только воспользоваться всеми найденными соотношениями и заметить что-то хорошее. Попробуйте выразить через них АВ и KB. А дальше останется только простой счёт углов!

Показать ответ и решение

Пусть $M$ и $N$ — середины отрезков $AC$ и $BC$ соответственно, $α = ∠ABC$ . Тогда $MN$ — средняя линия треугольника $ABC, MN ∥AB$ . Поскольку точка $K$ лежит на серединном перпендикуляре в $AC$ , отрезки $KA$ и $KC$ равны, откуда $∠KAC =∠KCA = α$ .

$PIC$

В силу условия

SKBL KL ⋅LB LB LM 2 = SAML-= LM-⋅AL-⇔ AL-= 2⋅KL-.

Так как $KL$ — биссектриса треугольника $AKB$ , мы получим

LB-= KB-. AL AK

Кроме того,

2⋅ LM = 2⋅ BN-= BC-. KL KB KB

Тогда из этих двух соотношений

KB- KB- LB- LM- BC- 2 CK = AK = AL = 2⋅KL = KB ⇒ KB =BC ⋅CK.

Треугольники $ABC$ и $KAC$ подобны по двум углам, откуда

CK AB AB- = BC-⇒ AB2 =BC ⋅CK

Поэтому $KB =AB$ , то есть треугольник $ABK$ равнобедренный. Заметим, что

∠BAK = ∠CAK − ∠CAB = α− (180∘− 2α)= 3α − 180∘,∠AKB = 180∘− 2α.

Мы получаем $∘ ∘ 3α− 180 =180 − 2α$ , откуда $∘ α =72$ . Таким образом, углы $ABC$ и $ACB$ равны $∘ 72$ , а угол $BAC$ равен $36∘$ .

Ответ:

$36∘,72∘,72∘$

Ошибка.
Попробуйте повторить позже

Задача 8#87883

Окружность, проходящая через вершины $A$ и $B$ остроугольного треугольника $ABC$ , пересекает стороны $AC$ и $BC$ в точках $P$ и $Q$ соответственно, а также проходит через центр описанной около треугольника $PQC$ окружности. Отрезки $AQ$ и $BP$ пересекаются в точке $K$ , а $∠ACB = 2∠AKP$ . Найдите $∠ACB$ .

Показать ответ и решение

Пусть $∠AKP =x.$ По условию $∠ACB = 2∠AKP = 2x.$

Рассмотрим дугу $⌣ PQ$ описанной окружности $△PCQ.$ Опирающийся на неё центральный угол $∠P OQ$ будет в два раза больше вписанного угла $∠PCQ.$ Значит, $∠POQ = 4x.$

$PIC$

Перейдём к рассмотрению окружности, проходящей через точки $A$ и $B.$ Можно найти величину дуги $PABQ,$ так как мы знаем вписанный угол $∠POQ$ , опирающийся на неё.

⌣ PABQ = 2∠POQ = 8x

С другой стороны, $⌣ PABQ$ можно представить в виде суммы дуг $⌣ PA,⌣AB$ и $⌣ BQ.$

Угол $∠AKP$ между хордами $AQ$ и $BP$ находится как

∠AKP = ⌣-AP+-⌣-BQ- 2

Тогда $⌣ AP+ ⌣BQ = 2∠AKP = 2x.$

Вычислим величину дуги $⌣AB.$ Используя угол $∠PKQ =180∘− x,$ заключенный между хордами $AQ$ и $BP$ , получим

⌣ AB+ ⌣P Q= 2∠PKQ = 360∘− 2x

Угол $∠ACB$ между секущими $AP$ и $QB$ находится как

∠ACB = ⌣-AB−-⌣P-Q- 2

Поэтому $⌣AB − ⌣P Q= 2∠ACB = 4x.$

Cложим последние два равенства и получим

(⌣AB+ ⌣P Q)+(⌣ AB− ⌣ PQ)= (360∘− 2x)+ 4x

⌣ AB = 180∘+ x

Теперь выражаем $⌣ PABQ$ через сумму дуг:

⌣ PABQ = (⌣P A+ ⌣BQ )+ ⌣ AB =2x +(180∘+ x)= 180∘+ 3x

Но в самом начале мы показали, что $⌣ PABQ = 8x.$ Значит,

∘ 8x= 180 +3x

x= 36∘

Тогда $∠ACB = 2x =72∘.$

Ответ:

$72∘$

Ошибка.
Попробуйте повторить позже

Задача 9#88173

Две окружности касаются внутренним образом в точке $K$ . В большей окружности проведена хорда $AB$ , касающаяся меньшей окружности в точке $L$ . Найдите $BL,$ если $AL = 10$ и $AK :BK = 2:5.$

Источники: Ломоносов - 2011, 11.5 и Бельчонок - 2019, 11.3

Показать ответ и решение

Покажем, что $KL$ является биссектрисой угла $AKB$ (это утверждение называется леммой Архимеда и при правильной формулировке может быть использовано на олимпиаде без доказательства). Тогда по свойству биссектрисы получим

BL- = BK--= 5 BL = 5⋅10= 25 AL AK 2 2

______________________________________________________________________________________________________

Способ 1. Пусть общая касательная к окружностям пересекает прямую $AB$ в точке $S$ . Пусть $∠SKA = α,∠AKL =β$ Отрезки $SK$ и $SL$ равны как отрезки касательных, проведенных из точки $S$ к меньшей окружности, следоваетельно, $∠SLK = ∠SKL =∠SKA + ∠AKL = α+ β$ .

По теореме об угле между касательной и хордой верно, что $∠KBA = ∠SKA = α$ . Наконец, по теореме о внешнем угле в треугольнике $LKB$ , $∠LKB = ∠KLA − ∠KBL =(α +β) − α = β$ .

$PIC$

_______________________________________________________________________________________________________

Способ 2. Рассмотрим гомотетию с центром в точке $K$ , переводящую меньшую окружность в большую. Пусть прямая $KL$ пересекает большую окружность в точке $W$ , тогда прямая $AB$ под действием гомотетии переходит в касательную к большей окружности, проведенную в точке $W$ . Таким образом, данная касательная паралельна $AB$ , то есть $W$ является серединой меньшей дуги $AB$ большей окружности.

$PIC$

_______________________________________________________________________________________________________

Способ 3. Пусть $W$ — середина меньшей дуги окружности $AB$ большей окружности. Рассмотрим инверсию с центром в точке $W$ и радиусом $W A$ . Точки $A$ и $B$ под действием инверсии останутся на месте, следовательно, прямая AB переходит в окружность, проходящую через точки $A$ , $B$ , и центр окружности инверсии — $W$ , то есть в большую окружность. Наконец, меньшая окружность переходит в окружность, которая касается образа большей окружности и образа прямой $AB$ и гомотетична своему пробразу с центром в $W$ , то есть остается на месте, то есть точка $L$ перейдет в точку $K$ , а значит, прямая $KL$ проходит через центр инверсии — $W$ .

$PIC$

Ответ: 25

Ошибка.
Попробуйте повторить позже

Задача 10#88171

Дан прямоугольный треугольник $ABC$ . На продолжении гипотенузы $BC$ выбрана точка $D$ так, что прямая $AD$ — касательная к описанной окружности $ω$ треугольника $ABC$ . Прямая $AC$ пересекает описанную окружность треугольника $ABD$ в точке $E$ . Оказалось, что биссектриса угла $ADE$ касается окружности $ω$ . В каком отношении точка $C$ делит отрезок $AE?$

Подсказки к задаче

Подсказка 1

На картинке есть две окружности, а также касательная к одной из них. Отметим равные углы, используя свойство вписанных углов и угла между хордой и касательной.

Подсказка 2

Получили, что треугольник АDE равнобедренный! В нем проведена биссектриса, и получается, что вследствие равнобедренности про неё сразу можно много что сказать.

Подсказка 3

Обратим внимание на треугольник DAK (если отметить пересечение биссектрисы ∠ADE с AE за К). Предыдущие рассуждения приводят к тому, что в нем угол А угол D получаются связанными между собой (помимо того, что в сумме эти углы дают π/2). Воспользуемся связью и явно найдем эти углы!

Подсказка 4

Осталось воспользоваться свойствами треугольника с углами 30,60,90 и выразить искомое соотношение!

Показать ответ и решение

Пусть $α =∠ABD,$ $K$ и $L$ — точки пересечения биссектрисы угла $∠ADE$ с $AE$ и $ω$ соответственно, $O$ — центр $ω$ . Угол между касательной $AD$ к окружности $ω$ и хордой $AC$ равен вписанному углу, который опирается на $AC,$ откуда $∠DAE = α.$ Кроме того, вписанные углы $∠AED$ и $α$ опираются на хорду $AD$ и поэтому равны. Тогда $∠DAE = ∠AED = α$ и треугольник $ADE$ равнобедренный. Поэтому биссектриса $DK$ является также его медианой и высотой. Значит, $AB ∥ DL$ , поскольку $AB$ и $DL$ перпендикулярны $AE$ .

$PIC$

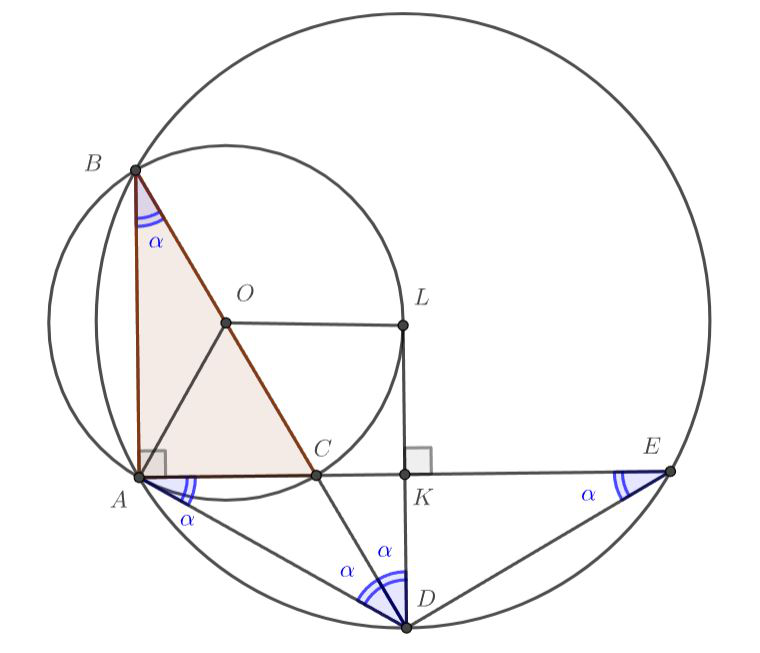
Прямоугольные треугольники $AOD$ и $LOD$ равны по катету и гипотенузе, откуда $∠ADO = ∠LDO = α.$ Из прямоугольного треугольника $ADK$ мы получаем, что $3α =90∘$ и $α= 30∘.$ Тогда $AD =2DK,$ и по свойству биссектрисы