.04 КПВ - задачи
Ошибка.
Попробуйте повторить позже
Великие стеклодувы Адриан, Бенни и Вальдемар выдувают из стекла,
общий запас которого равен 16, три вида фигурок: икс(), игрек(
) и
дзет(
).
Технология производства фигурок представлена в таблице:
| Стеклодув | |||
| Андриан | 1 | 2 | 4 |
| Бенни | 1 | 4 | 2 |
| Вальдемар | 2 | 1 | 4 |
где – количество единиц
-го типа фигурок, которое способен изготовить
стеклодув из 1 единицы стекла.
а) Выведите уравнение КПВ цеха, считая, что стекло можно распределить в любой пропорции между работниками.
б) Известно, что КПВ соседнего цеха описывается уравнением
(стеклодувы из второго цеха не умеют производить фигурки типа икс). Фабрика
продает фигурки только наборами, состоящими из фигурок всех типов в
пропорции
.
Какое максимальное целое количество наборов сможет изготовить фабрика, если стекло нельзя транспортировать между цехами?
а) Заметим, что для производства Андрианом единиц икса необходимо
единиц стекла, для
производства
единиц игрека необходимо
единиц стекла, а для производства
дзетов
соответственно
единиц стекла. Из ограничения на количество стекла выведем уравнения КПВ
каждого работника (они нам ещё пригодятся), если
-ому работнику выделили
единиц
стекла.
|
|
Утверждение 1. Фигурки икс Вальдемар производит с наименьшими издержками относительно
ресурса, а значит он будет производить весь икс (,
).
Утверждение 2. Фигурки игрек Бенни производит с наименьшими издержками относительно ресурса,
а значит он будет производить весь ирек (,
).
Утверждение 3. Фигурки дзет Бенни производит большими издержками относительно
ресурса, чем это делает Адриан и Вальдемар, а значит Бенни не будет производить дзет
().
Система примет вид:
|
|
Сложим первые три уравнения:
б) Введем индексы: КПВ первого цеха: , КПВ второго цеха:
.
Пусть количество комплектов равно
, тогда
.
В этом случае уравнения КПВ двух цехов примут вид:
|
|
Сложим двумерные КПВ классическим образом при фиксированном . Тогда КПВ фабрики
описывается:
|
|
где ,
.
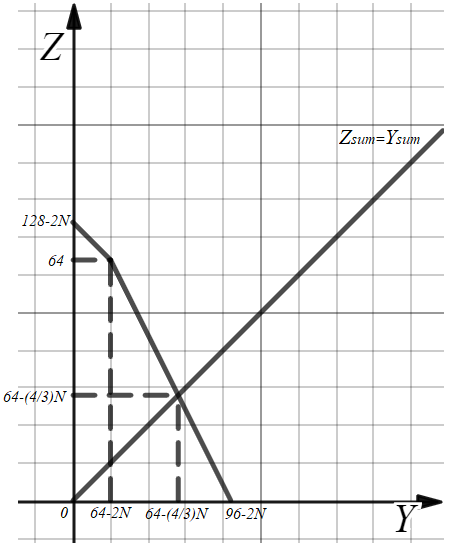
Заметим, что луч , проходит ниже точки
, поэтому необходимо
рассмотреть второй участок КПВ (
). Не трудно почитать, что КПВ
пересекается с лучом
в точке
.
Точка должна лежат левее точки
– это является условием того, что
необходимую пропорцию производства удастся соблюсти. Откуда
. С учетом
целочисленности максимальное количество товаров, которое способна произвести фабрика, равно
27.
Чтобы достичь такого выпуска, можно установить .
Так как ресурсы в оптимуме тратятся не полностью можно рассмотреть массу примеров
распределения.
Ответ: а) ; б) 27.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




