.04 Международная торговля в микромоделях - задачи
Ошибка.
Попробуйте повторить позже
Рассмотрим фирму, реализующую продукцию на двух рынках: внутреннего монопольного со спросом
и внешнего, на котором можно продать любое количество продукции по цене
ден.
единиц. Общие издержки фирмы описываются функцией
Постройте в координатах множество решений об экспортных поставках, которые принимает
фирма при различных значениях
.
Функция прибыли при производстве :
Подставим обратную функцию внутреннего спроса :
Заметим, что относительно функция прибыли – парабола с ветвями вниз, а значит оптимально
находится в вершине:
Однако, важно заметить, что в условиях оптимально
.
Подставим найденную вершину в целевую функцию прибыли
Раскрываем скобки:
Окончательно:
Оптимизация по : функция прибыли является квадратичной по
:
Вершина параболы с ветвями вниз:
Учтем ряд ограничений:
1. При :
→ оптимально
2. При :
→ оптимально
3. При : предельный доход от экспорта (
) превышает максимально возможный
предельный доход от продаж на внутреннем рынке (
). Поэтому фирма: полностью
прекращает продажи на внутреннем рынке (
) и производит только для экспорта, объем
производства определяется из условия
:
,
.
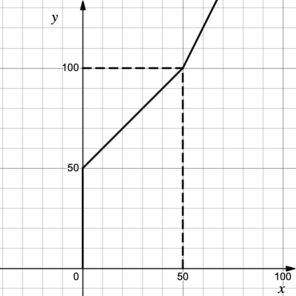
Множество решений (предложение экспорта на мировой рынок):
|
|
Итоговый график в координатах :
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




