Алгебра. "Гвозди" для квадратичной функции
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет корни, причём все корни больше трёх.
Подсказка 1
Нарисуем график! Мы знаем, что это парабола ветвями вверх. Какие необходимые и достаточные условия нужно наложить на график, чтобы оба корня нашего уравнения были больше 3?
Подсказка 2
Абсцисса вершины параболы должна быть правее 3; дискриминант больше нуля; значение в точке 3 положительно
Подсказка 3
У нас получилась система из трёх уравнений относительно а, осталось лишь решить её и получить область возможных значений параметра!
Квадратное уравнение имеет корни, если его дискриминант неотрицателен.
Если уравнение имеет единственный корень, который совпадает с
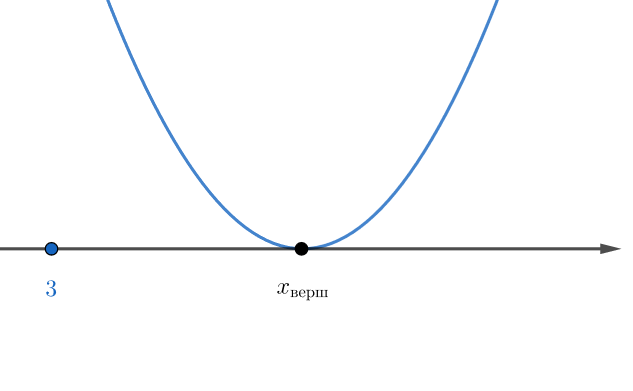
Если то уравнение имеет два корня. При условии, что оба корня
график выглядит так:
![]()
Условия на параболу, фиксирующие оба подходящих случая, можно записать системой:
Подставим выражения для дискриминанта, абсциссы вершины и значения в точке
Решение системы:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




