Исследование области значений функции (в том числе a = f(x))
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет единственный корень.
Подсказка 1
а входит только в первой степени, поэтому удобно будет перенести а направо и нарисовать получившееся уравнение в плоскости хОа!
Подсказка 2
Изобразим график функции а(x) = 2x³ + x²/2 - x - 1. Как можно изобразить график кубической функции?
Подсказка 3
С помощью производной! Определим промежутки возрастания и убывания функции, посчитаем значение функции в точках перегиба. Осталось лишь "двигать" горизонтальную прямую, соответствующую разным значениям а, и искать ровно одно пересечение!
Рассмотрим функцию и построим её эскиз. Для этого возьмём производную:
По знакам производной определяем промежутки возрастания и убывания функции:
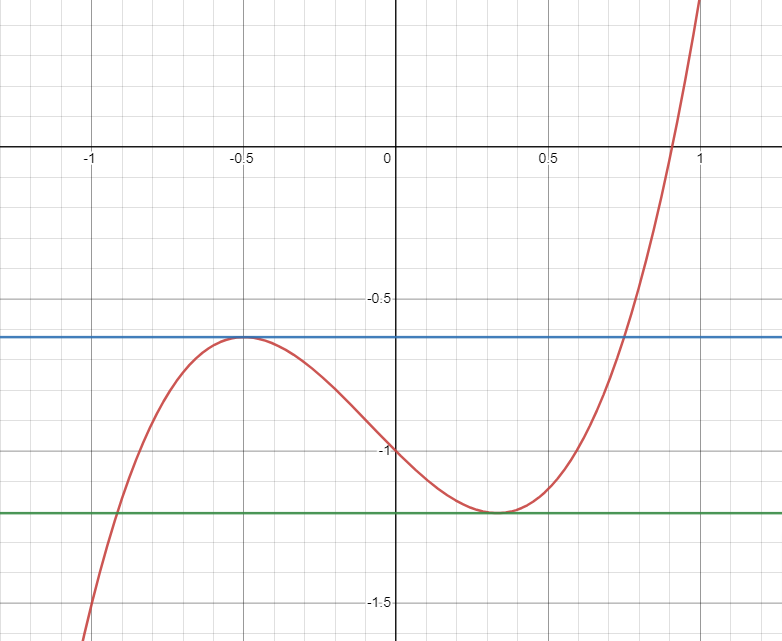
Найдём и
При
и
прямая
пересекает
график
ровно в одной точке, при других значениях параметра
точек пересечения больше одной.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




